Problem - 1660E - Codeforces

你会得到一个大小为n×n的二进制矩阵A。行从上到下从1到n编号，列从左到右从1到n编号，位于第i行和第j列交点的元素称为Aij。考虑一组4个操作。

循环地将所有行向上移动。索引为i的行将被写在i-1行的位置上（2≤i≤n），索引为1的行将被写在n行的位置上。
循环地将所有的行向下移动。索引i的行将被写在i+1行的位置（1≤i≤n-1），索引n的行将被写在1行的位置。
循环地将所有列向左移动。索引为j的列将被写在j-1列的位置上（2≤j≤n），索引为1的列将被写在n列的位置上。
循环地将所有的列向右移动。索引j的列将被写在j+1列的位置上(1≤j≤n-1)，索引n的列将被写在1列的位置上。
3×3矩阵在左边显示的是进行3次运算之前，右边显示的是进行3次运算之后。
你可以对矩阵进行任意数量（可能是零）的操作；这些操作可以按任何顺序进行。

之后，你可以执行任意数量（可能为零）的新的xor-操作。

选择任何元素Aij并赋予其新的值Aij⊕1。换句话说，(Aij+1)mod2的值将被写入元素Aij中。
每次应用这个xor操作都要花费一个burl。请注意，4个移位操作--是免费的。这4个操作只能在进行xor-操作之前进行。

输出为使A矩阵单一化所需的最小布尔数。单一矩阵是指主对角线上有1，其余元素为0的矩阵（也就是说，如果i=j，Aij=1，否则Aij=0）。

输入
输入的第一行包含一个整数t（1≤t≤104）--测试中测试案例的数量。

接下来是测试用例的描述。在每个测试用例之前，在输入中写一个空行。

每个测试用例的第一行包含一个数字n (1≤n≤2000)

接下来是n行，每行正好包含n个字符，并且只由0和1组成。这些行描述了矩阵中各元素的值。

保证所有测试案例的n2值之和不超过4⋅106。

输出
对于每个测试用例，输出为使A矩阵单元化所需的最小布尔数。换句话说，在对矩阵进行循环移位后，打印出使A矩阵成为单数所需的最小xor操作数。

例子
输入复制
4

3
010
011
100

5
00010
00001
10000
01000
00100

2
10
10

4
1111
1011
1111
1111
outputCopy
1
0
2
11
注意
在第一个测试案例中，你可以这样做：首先，将所有的行循环下移，然后矩阵的主对角线将只包含 "1"。然后有必要对唯一不在主对角线上的 "1 "进行xor操作。

在第二个测试案例中，你可以通过对矩阵应用操作2--行的循环上移两次来制造一个单元矩阵。

题解:

根据四种变化我们发现,他是整体变化的,

无论如何变化,所有正对角上的点是不变的

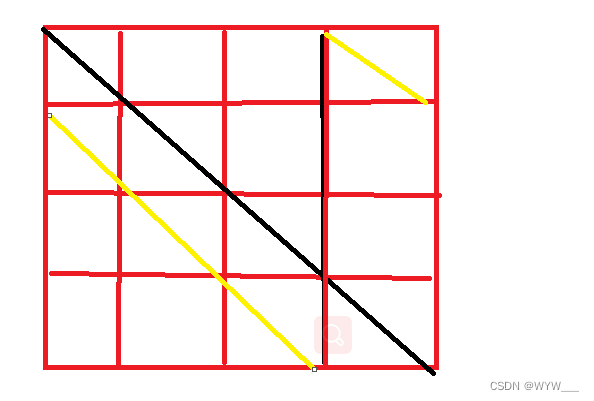
 黄色的也是我所说的正对角线(类似黄色与黑色的都是)

所以我们遍历这些对角线即可,找到1最多的

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define int long long
//1 1 3 3 3
char a[2005][2005];
void solve()
{
	int n;
	cin >> n;
	int s = 0;
	for(int i = 0;i < n;i++)
	{
		for(int j = 0;j < n;j++)
		{
			cin >> a[i][j];
			if(a[i][j] == '1')
			{
				s++;
			}
		}
	}
	int ans = 0;
	for(int i = 0;i < n;i++)
	{
		int k = 0,tmp = 0;
		for(int j = i;k < n;k++,j = (j+1)%n)
		{
			if(a[k][j] == '1')
			{
				tmp++;
			}
		}
		ans = max(tmp,ans);
	} 
	cout<<n - ans + s - ans<<"\n";
}
signed main()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);
//	cout.tie(0);
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}