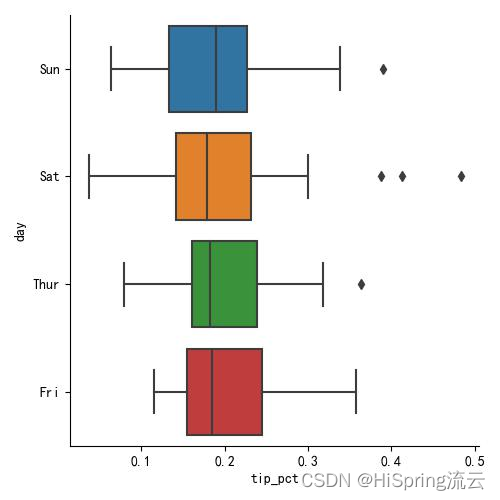
最优控制 3:使用极小值原理求解最优控制问题
- 引言
- 极小值原理
- 动态规划
- 连续系统 HJB 方程的推导
引言
经典变分法是一种特别强大的工具,但是它要求控制量必须可导且无界,这在很多问题中都是不成立的。着陆器的软着陆,卫星的姿态控制,等等。从主观上都可以分析出来,着陆器的软着陆控制,肯定是先让着陆器自由落体,然后从某一个高度开始反向喷气,最后落地一瞬间速度刚好为0。卫星的姿态控制肯定是当姿态有偏差时,用最大力矩控制一次,然后让卫星通过惯性 “转” 一段时间再反向最大力矩控制一次。这个过程控制量肯定是不可导的。
因此,有很多最优控制问题,不能用变分法解决。所以,极小值原理和动态规划是比变分法更强大的工具。本文将介绍这两种理论,下一篇博客将给出变分法、极小值原理和动态规划在解决最优控制问题时的等价性推导。(当然,前提是这个最优控制问题本身可以用三种方法去解决才行;如果某个问题不能用变分法,那谈等价性是没有意义的。)
极小值原理
在计算和使用的时候,极小值原理和变分法的公式很相似,只不过在哈密顿函数上做了改变。因为 u u u 可能不可导,所以就没有 ∂ H ∂ u = 0 \frac{\partial H}{\partial u}=0 ∂u∂H=0 了,而是用别的方程或不等式去约束。下面直接通过一个问题的形式给出极小值原理。
问题:
min
u
(
t
)
∈
Ω
J
=
φ
[
x
(
t
f
)
,
t
f
]
+
∫
t
0
t
f
L
[
x
(
t
)
,
u
(
t
)
,
t
]
d
t
s
.
t
.
x
˙
(
t
)
=
f
[
x
(
t
)
,
u
(
t
)
,
t
]
,
x
(
t
0
)
=
x
0
,
ψ
[
x
(
t
f
)
,
t
f
]
=
0
\begin{align} \begin{aligned} & \min_{u(t)\in\Omega}{J=\varphi\left[x(t_f),t_f\right]+\int_{t_0}^{t_f}{L\left[x(t), u(t), t\right]}dt}\\ & s.t.\quad \dot{x}(t)=f\left[x(t), u(t), t\right], x(t_0)=x_0,\psi\left[x(t_f), t_ f\right]=0 \end{aligned} \end{align}
u(t)∈ΩminJ=φ[x(tf),tf]+∫t0tfL[x(t),u(t),t]dts.t.x˙(t)=f[x(t),u(t),t],x(t0)=x0,ψ[x(tf),tf]=0
由极小值原理,该问题实现最优控制的必要条件是:
- 最优状态
x
∗
(
t
)
x^*(t)
x∗(t) 和最优协状态
λ
∗
(
t
)
\lambda^*(t)
λ∗(t) 满足正则方程 (这里与变分法是一样的)
λ ˙ ∗ ( t ) = − ∂ H ( x ∗ , u ∗ , λ ∗ , t ) ∂ x x ˙ ( t ) = ∂ H ( x ∗ , u ∗ , λ ∗ , t ) ∂ λ = f [ x ∗ ( t ) , u ∗ ( t ) , t ] \begin{align} \begin{aligned} \dot{\lambda}^*(t)&=-\frac{\partial H(x^*,u^*,\lambda^*,t)}{\partial x}\\ \dot{x}(t)&=\frac{\partial H(x^*,u^*,\lambda^*,t)}{\partial \lambda}=f\left[x^*(t),u^*(t), t\right] \end{aligned} \end{align} λ˙∗(t)x˙(t)=−∂x∂H(x∗,u∗,λ∗,t)=∂λ∂H(x∗,u∗,λ∗,t)=f[x∗(t),u∗(t),t]
其中, H ( x , u , λ , t ) = L [ x ( t ) , u ( t ) , t ] + λ T ( t ) f [ x ( t ) , u ( t ) , t ] H(x,u,\lambda,t)=L\left[x(t), u(t), t\right]+\lambda^T(t)f\left[x(t), u(t), t\right] H(x,u,λ,t)=L[x(t),u(t),t]+λT(t)f[x(t),u(t),t] 为哈密顿函数。 - 在最优状态 最优控制 以及最优协变量上,对应的哈密顿函数取得最小值
Tips: 这里与变分法不一样了,因为 ∂ H ∂ u = 0 \frac{\partial H}{\partial u}=0 ∂u∂H=0 不一定成立。一方面,导数不一定存在;另一方面,极值点对应的 u u u 不一定在容许控制范围内。
H ( x ∗ ( t ) , u ∗ ( t ) , λ ∗ ( t ) , t ) = min u ( t ) ∈ Ω H ( x ∗ ( t ) , u ( t ) , λ ∗ ( t ) , t ) \begin{align} \begin{aligned} H(x^*(t), u^*(t), \lambda^*(t) ,t)=\min_{u(t)\in\Omega}{H(x^*(t), u(t), \lambda^*(t) ,t)} \end{aligned} \end{align} H(x∗(t),u∗(t),λ∗(t),t)=u(t)∈ΩminH(x∗(t),u(t),λ∗(t),t) - 边界条件与横截条件
x ∗ ( t 0 ) = x 0 ψ [ x ∗ ( t f ) , t f ] = 0 λ ∗ ( t f ) = ∂ φ ∂ x ( t f ) + ∂ ψ T ∂ x ( t f ) ⋅ γ \begin{align} \begin{aligned} x^*(t_0) &= x_0\\ \psi\left[x^*(t_f), t_f\right] &= 0\\ \lambda^*(t_f) &= \frac{\partial \varphi}{\partial x(t_f)} + \frac{\partial \psi^T}{\partial x(t_f)}\cdot\gamma \end{aligned} \end{align} x∗(t0)ψ[x∗(tf),tf]λ∗(tf)=x0=0=∂x(tf)∂φ+∂x(tf)∂ψT⋅γ - 当
t
f
t_f
tf 自由时,哈密顿函数还要满足终端时刻的横截条件
H ( t f ∗ ) = − ∂ φ ∂ t f − γ T ∂ ψ ∂ t f \begin{align} \begin{aligned} H(t_f^*)=-\frac{\partial \varphi}{\partial t_f} - \gamma^T\frac{\partial \psi}{\partial t_f} \end{aligned} \end{align} H(tf∗)=−∂tf∂φ−γT∂tf∂ψ
下边直接给出不同条件下的极小值原理的必要条件的表格:
t f t_f tf 固定的情况

t f t_f tf 自由的情况

动态规划
动态规划也可以用来解决最优控制问题,但是它最初是被设计用来解决多级决策问题的。比如一个地图,好多节点,研究怎么走代价最小的问题。它的公式看起来其实并不是像是控制领域的算法,更像是计算机领域的。它后来被扩展到离散系统的最优控制问题,每一个时间步就是一次决策。比如一共 10 秒,每秒钟 100 次,那么一共就是 1000 次决策,如果这1000次都是最优的,那么最后结果一定是最优的。
更进一步地,如果已知从 960 步到 1000 步的最优决策 u 960 − 1000 ∗ u^*_{960-1000} u960−1000∗,那么不论前边 959 步怎么控制,只要到第 960 步的时候,从 960 步到 1000 步的最优决策一定是 u 960 − 1000 ∗ u^*_{960-1000} u960−1000∗。这便是动态规划的核心:寻找最优子问题和重叠的子结构。很多计算机领域的经典问题都可以用动态规划建模和解决。(汉诺塔,走台阶等等,不搞计算机,不懂)
所以,一般情况下,基于动态规划的控制方法都是从后往前逆序求解的。先算第 1000 个最优决策是啥,然后算第 999 个,最后一步一步反推回第 1 个。仿真或者应用的时候再从第 1 个到第 1000 个顺序执行。典型的例子就是线性二次型最优控制 (LQR),这种问题是有解析解的。
当然动态规划也有连续系统的版本,它就是大名鼎鼎的 HJB 方程。HJB 方程揭示了所有最优控制问题的本质,并且只要解出 HJB 方程,最优控制问题就解决了 (当然前提是有解)。问题就在于有很多非线性的最优控制问题,或者模型不确定的最优控制问题,我们明知道 HJB 方程的解存在且唯一,但就是找不到。由此也衍生出一个新兴的控制方法 (理论):自适应动态规划 (Adaptive Dynamic Programming),也叫近似动态规划 (Approximate Dynamic Programming)。它的另外一个名字比较接地气:强化学习控制。只不过说强化学习控制一般是从计算机的角度看这个问题,说 ADP 一般是从控制理论的角度看这个问题。扯远了…
连续系统 HJB 方程的推导
最优控制问题与 (1) 中所描述的相同。考虑到动态规划中的 “时序逆推” 的概念,取
J
[
x
(
t
)
,
t
]
=
φ
[
x
(
t
f
)
,
t
f
]
+
∫
t
t
f
L
[
x
(
τ
)
,
u
(
τ
)
,
τ
]
d
τ
\begin{align} \begin{aligned} J\left[x(t), t\right] = \varphi\left[x(t_f), t_f\right] + \int_{t}^{t_f}{L\left[x(\tau), u(\tau), \tau\right]}d\tau \end{aligned} \end{align}
J[x(t),t]=φ[x(tf),tf]+∫ttfL[x(τ),u(τ),τ]dτ
记为从
t
t
t 时刻到
t
f
t_f
tf 时刻的代价函数,这个问题最终的目的是要求出
J
[
x
0
,
t
0
]
J\left[x_0, t_0\right]
J[x0,t0]。
改写 (6),得到
J
[
x
(
t
)
,
t
]
=
∫
t
t
+
δ
t
L
[
x
(
τ
)
,
u
(
τ
)
,
τ
]
d
τ
+
φ
[
x
(
t
f
)
,
t
f
]
+
∫
t
+
δ
t
t
f
L
[
x
(
τ
)
,
u
(
τ
)
,
τ
]
d
τ
=
∫
t
t
+
δ
t
L
[
x
(
τ
)
,
u
(
τ
)
,
τ
]
d
τ
+
J
[
x
(
t
+
δ
t
,
t
+
δ
t
)
]
\begin{align} \begin{aligned} J\left[x(t), t\right] &= \int_{t}^{t+\delta t}{L\left[x(\tau), u(\tau), \tau\right]}d\tau+\varphi\left[x(t_f), t_f\right] + \int_{t+\delta t}^{t_f}{L\left[x(\tau), u(\tau), \tau\right]}d\tau\\ &=\int_{t}^{t+\delta t}{L\left[x(\tau), u(\tau), \tau\right]}d\tau+J\left[x(t+\delta t, t+\delta t)\right] \end{aligned} \end{align}
J[x(t),t]=∫tt+δtL[x(τ),u(τ),τ]dτ+φ[x(tf),tf]+∫t+δttfL[x(τ),u(τ),τ]dτ=∫tt+δtL[x(τ),u(τ),τ]dτ+J[x(t+δt,t+δt)]
上式右边第一项应用积分中值定理,第二项应用 Taylor 展开,得到
J
[
x
(
t
)
,
t
]
=
∫
t
t
+
δ
t
L
[
x
(
τ
)
,
u
(
τ
)
,
τ
]
d
τ
+
J
[
x
(
t
+
δ
t
,
t
+
δ
t
)
]
=
L
[
x
(
t
+
α
δ
t
)
,
u
(
t
+
α
δ
t
)
,
t
+
α
δ
t
]
δ
t
+
J
[
x
(
t
)
,
t
]
+
∂
J
T
∂
x
δ
x
+
∂
J
∂
t
δ
t
=
L
[
x
(
t
+
α
δ
t
)
,
u
(
t
+
α
δ
t
)
,
t
+
α
δ
t
]
δ
t
+
J
[
x
(
t
)
,
t
]
+
∂
J
T
∂
x
d
x
(
t
)
d
t
δ
t
+
∂
J
∂
t
δ
t
\begin{align} \begin{aligned} J\left[x(t), t\right] &=\int_{t}^{t+\delta t}{L\left[x(\tau), u(\tau), \tau\right]}d\tau+J\left[x(t+\delta t, t+\delta t)\right]\\ &=L\left[x(t+\alpha\delta t), u(t+\alpha\delta t), t+\alpha\delta t\right]\delta t+J\left[x(t), t\right]\\ & + \frac{\partial J^T}{\partial x}\delta x + \frac{\partial J}{\partial t}\delta t\\ &=L\left[x(t+\alpha\delta t), u(t+\alpha\delta t), t+\alpha\delta t\right]\delta t+J\left[x(t), t\right]\\ &+ \frac{\partial J^T}{\partial x}\frac{dx(t)}{dt}\delta t + \frac{\partial J}{\partial t}\delta t \end{aligned} \end{align}
J[x(t),t]=∫tt+δtL[x(τ),u(τ),τ]dτ+J[x(t+δt,t+δt)]=L[x(t+αδt),u(t+αδt),t+αδt]δt+J[x(t),t]+∂x∂JTδx+∂t∂Jδt=L[x(t+αδt),u(t+αδt),t+αδt]δt+J[x(t),t]+∂x∂JTdtdx(t)δt+∂t∂Jδt
整理,得
L
[
x
(
t
+
α
δ
t
)
,
u
(
t
+
α
δ
t
)
,
t
+
α
δ
t
]
+
∂
J
T
∂
x
d
x
(
t
)
d
t
+
∂
J
∂
t
=
0
\begin{align} \begin{aligned} L\left[x(t+\alpha\delta t), u(t+\alpha\delta t), t+\alpha\delta t\right] + \frac{\partial J^T}{\partial x}\frac{dx(t)}{dt}+ \frac{\partial J}{\partial t}=0 \end{aligned} \end{align}
L[x(t+αδt),u(t+αδt),t+αδt]+∂x∂JTdtdx(t)+∂t∂J=0
令
δ
t
→
0
\delta t\rightarrow0
δt→0,并应用最优性原理,有
∂
J
∗
[
x
(
t
)
,
t
]
∂
t
=
−
min
u
∈
Ω
{
L
[
x
(
t
)
,
u
(
t
)
,
t
]
+
[
∂
J
∗
∂
x
]
T
f
[
x
,
u
,
t
]
}
\begin{align} \begin{aligned} \frac{\partial J^*\left[x(t), t \right]}{\partial t}=-\min_{u\in\Omega}{\left\{L\left[x(t), u(t), t\right] + \left[\frac{\partial J^*}{\partial x}\right]^Tf\left[x,u,t\right]\right\}} \end{aligned} \end{align}
∂t∂J∗[x(t),t]=−u∈Ωmin{L[x(t),u(t),t]+[∂x∂J∗]Tf[x,u,t]}
此时,定义哈密顿函数
H
[
x
(
t
)
,
u
∗
[
x
(
t
)
,
∂
J
∗
∂
x
,
t
]
,
∂
J
∗
∂
x
,
t
]
=
min
u
∈
Ω
H
[
x
(
t
)
,
u
(
t
)
,
∂
J
∗
∂
x
,
t
]
H\left[x(t), u^*\left[x(t), \frac{\partial J^*}{\partial x}, t\right], \frac{\partial J^*}{\partial x}, t\right]=\min_{u\in\Omega}{H\left[x(t), u(t), \frac{\partial J^*}{\partial x}, t\right]}
H[x(t),u∗[x(t),∂x∂J∗,t],∂x∂J∗,t]=u∈ΩminH[x(t),u(t),∂x∂J∗,t]
则,HJB 方程可以简写如下:
H
[
x
(
t
)
,
u
∗
[
x
(
t
)
,
∂
J
∗
∂
x
,
t
]
,
∂
J
∗
∂
x
,
t
]
+
∂
J
∗
∂
t
=
0
\begin{align} \begin{aligned} H\left[x(t), u^*\left[x(t), \frac{\partial J^*}{\partial x}, t\right], \frac{\partial J^*}{\partial x}, t\right]+\frac{\partial J^*}{\partial t}=0 \end{aligned} \end{align}
H[x(t),u∗[x(t),∂x∂J∗,t],∂x∂J∗,t]+∂t∂J∗=0
同时满足边界条件:
J
∗
[
x
(
t
f
)
,
t
)
f
]
=
φ
[
x
(
t
f
)
,
t
f
]
J^*\left[x(t_f), t)f\right]=\varphi\left[x(t_f), t_f\right]
J∗[x(tf),t)f]=φ[x(tf),tf]
至此,极小值原理与动态规划基本理论的学习笔记就结束了 (不放例题了,敲公式太麻烦了)。


![[C++]:万字超详细讲解多态以及多态的实现原理(面试的必考的c++考点)](https://img-blog.csdnimg.cn/04c16237ebb943a899981ce69e863a68.png)