1 前言

1.1 决策树的介绍

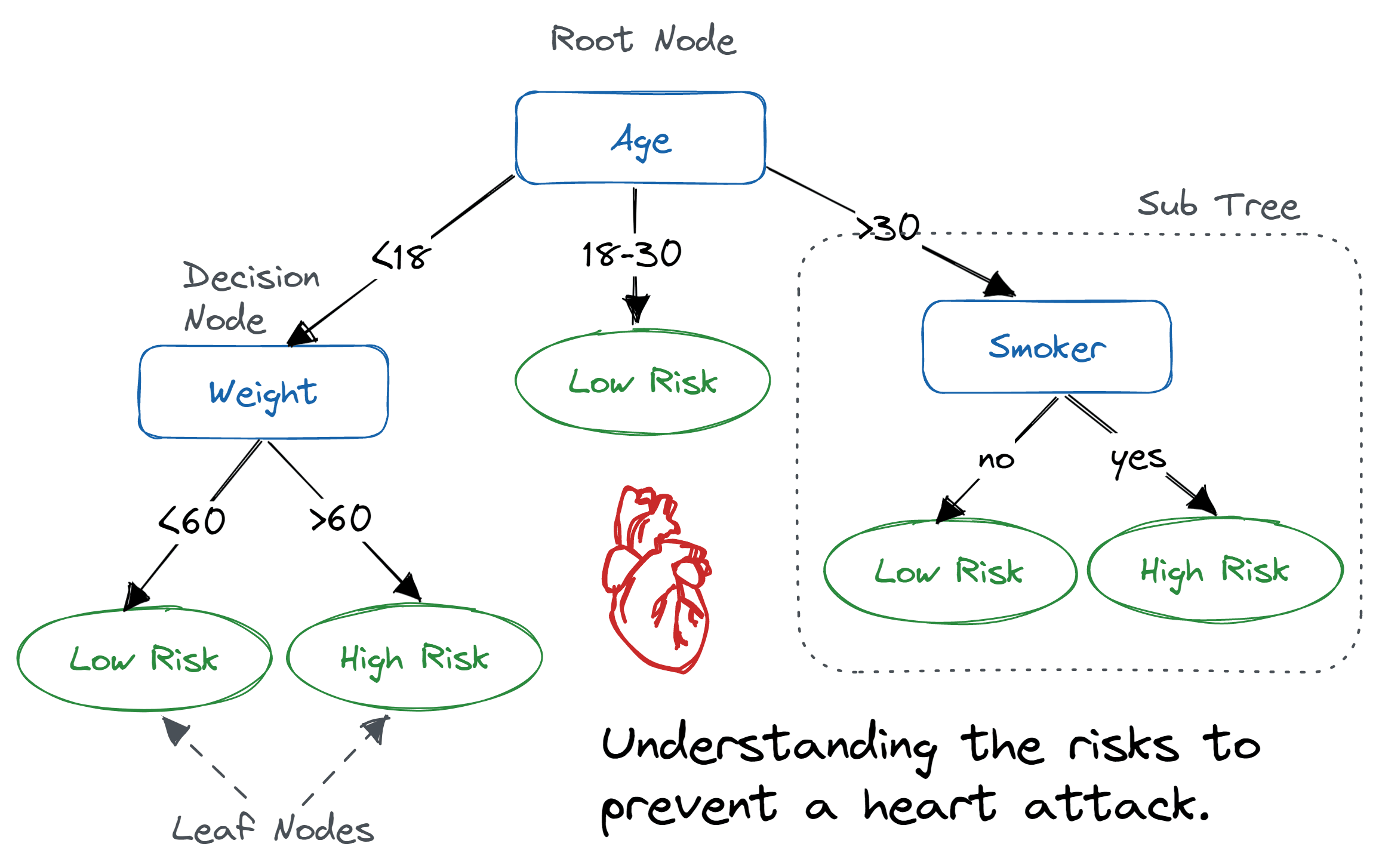
决策树（Decision Tree，DT）是一种类似流程图的树形结构，其中内部节点表示特征或属性，分支表示决策规则，每个叶节点表示结果。在决策树中，最上方的节点称为根节点。它学习基于属性值进行分区。它以递归方式进行分区，称为递归分区。这种类似流程图的结构有助于决策制定。它的可视化类似于流程图，可以很容易地模拟人类的思维过程。这就是为什么决策树易于理解和解释的原因。

决策树的时间复杂度是给定数据中记录和属性数量的函数。决策树是一种无分布或非参数方法，不依赖于概率分布假设。决策树可以很好地处理高维数据。

其原理可简单分为三步：**选择最优划分属性：**根据信息增益、信息增益比、基尼指数等方法，选择当前数据集中最优的属性作为划分属性，将数据集分成多个子集。**递归生成子树：**对每个子集重复步骤1，递归生成子树，直到所有的叶子节点都属于同一类别。**剪枝：**为了防止过拟合，需要对决策树进行剪枝，即去除一些分支或子树，使决策树更加简洁。

优点：

• 易于理解和解释：DT算法可以生成易于理解和解释的决策树模型，因此非专业人员也可以理解和使用该算法。

• 可解释性和可视化：DT算法可以通过绘制决策树的形式来直观地呈现分类过程，增强了模型的可解释性和可视化性。

• 适用性广泛：DT算法可以处理离散和连续型特征，且对数据的分布和噪声鲁棒性较高。

缺点：

• 容易过拟合：DT算法在训练集上可能表现得很好，但在测试集上表现得很差，容易过拟合。

• 对噪声和异常值比较敏感：DT算法对噪声和异常值比较敏感，容易导致生成的决策树过于复杂。

• 不支持在线学习：DT算法需要一次性加载所有的数据，并在内存中进行操作，因此不支持在线学习。

1.2 决策树的应用

决策树对于常规分类跟前面介绍的五种分类器其实差别不大，不过鉴于其易理解易运用对于实际生活还是有着不少便利。

1. 金融风险评估：决策树可以用于预测借款人的还款能力和信用等级，帮助金融机构决定是否批准贷款。

2. 医疗诊断：决策树可以用于帮助医生诊断疾病或推荐治疗方案，根据患者的症状和医疗历史进行分类。

3. 客户关系管理：决策树可以用于客户细分，根据客户的购买历史、偏好和行为预测客户的需求，帮助企业定制个性化的服务。

4. 电子商务：决策树可以用于商品推荐，根据用户的历史购买记录和行为推荐符合用户偏好的商品。

5. 生产优化：决策树可以用于优化生产过程，根据生产线上的各种因素，例如温度、湿度、时间等来决定何时停机、何时更换部件，从而减少故障和损失。

6. 人力资源管理：决策树可以用于招聘、晋升和培训决策，根据员工的学历、工作经验、业绩等因素，预测员工的发展潜力和能力，从而做出更加科学的决策。

2 Scikit-learn数据集演示

2.1 导入函数

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn import metrics 

2.2 导入数据

先下载这个糖尿病数据集：https://www.kaggle.com/datasets/uciml/pima-indians-diabetes-database

注册或者用google登陆一下download即可，若下载失败或者登不上去的可后台回复0420领取示例数据集

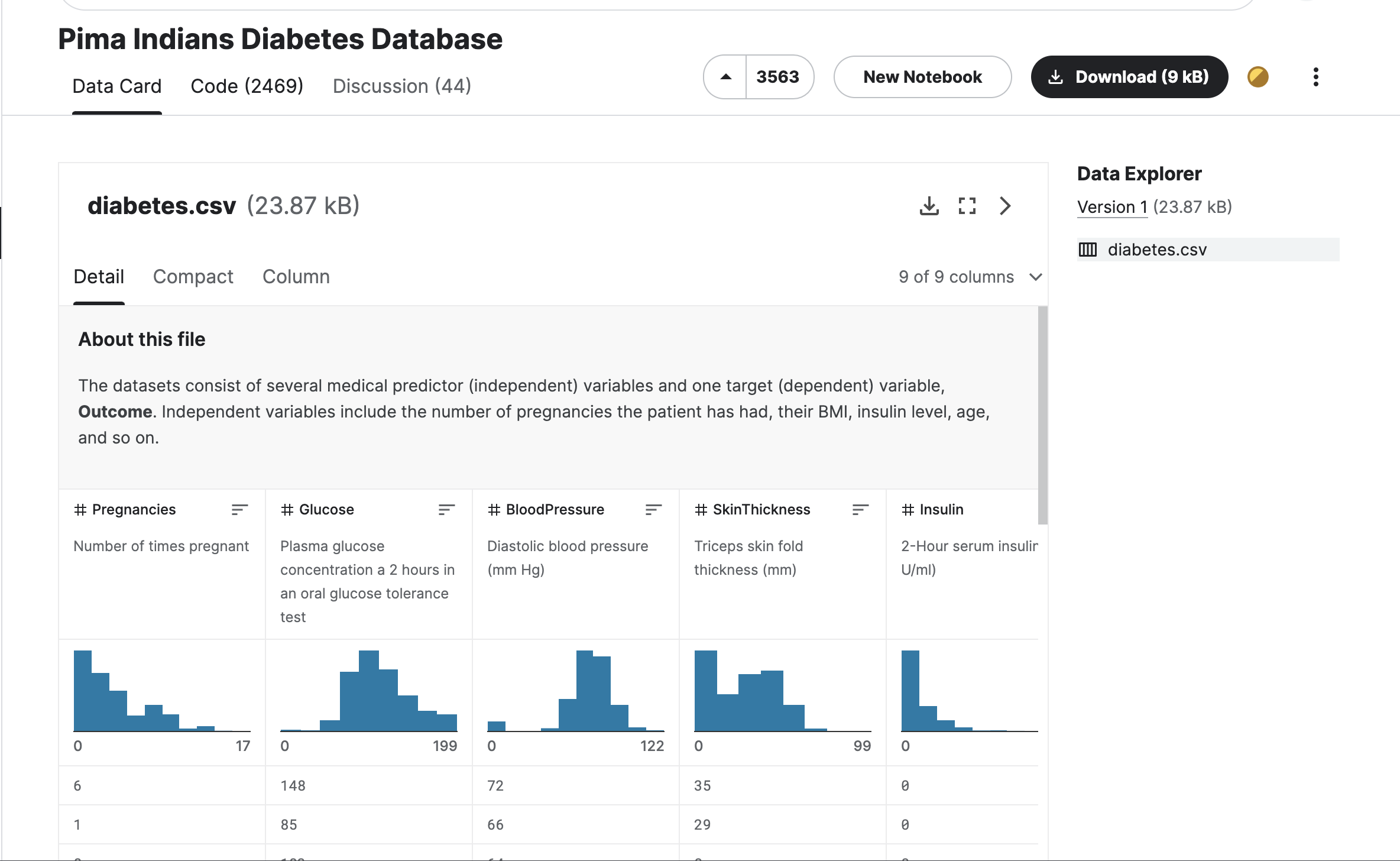
然后导入数据，这里用了小写表头，所以header=None，然后再将首行定义为列名，若参考网上其他教程，留意库和函数的更新更改，否则可能会报错

col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv("diabetes.csv", header=None, names=col_names)
pima = pima.iloc[1:]
pima.head()

2.3 建模

这里定义自变量和因变量，然后分组

feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable

# 训练集测试集7/3分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

建立决策树

clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)
y_pred = clf.predict(X_test)

2.4 评估模型

print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

结果能达到69.697%，还是可以的

2.5 可视化决策树

这两个包先下载了，且检查路径没问题

#!pip install graphviz
#!pip install pydotplus

可视化

from sklearn.tree import export_graphviz
from six import StringIO  
from IPython.display import Image  
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,  
                filled=True, rounded=True,
                special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())  
graph.write_png('diabetes.png')
Image(graph.create_png())

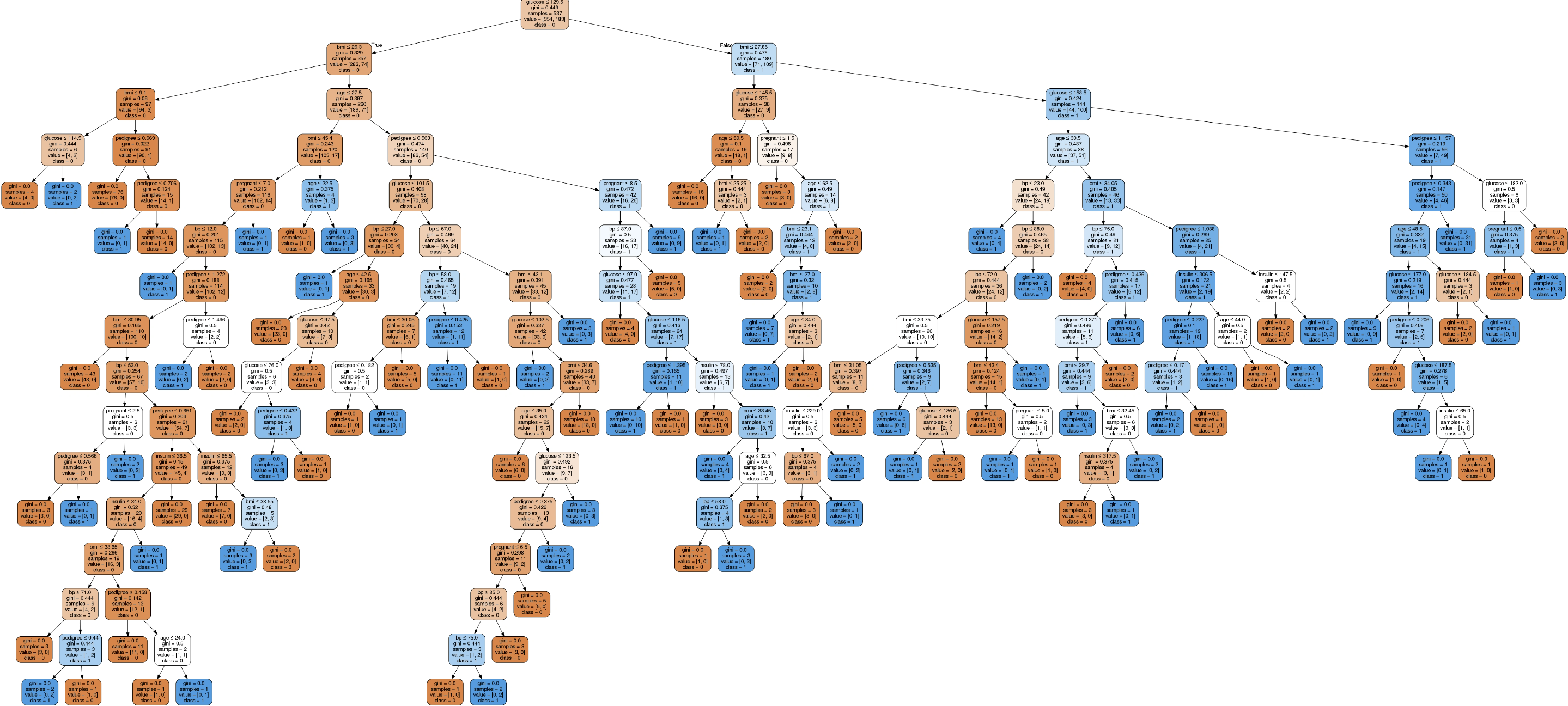
这是原始的分类，每个内部节点都有一个拆分数据的决策规则，称为基尼系数，测量节点的杂质，因此获取更准确的结果需要进行优化。

2.6 优化模型

• criterion: 可选参数（默认为“gini”）或选择属性选择度量。该参数允许我们使用不同的属性选择度量。支持的标准是“gini”，用于Gini指数，以及“entropy”，用于信息增益。

• splitter: 字符串，可选参数（默认为“best”）或分割策略。该参数允许我们选择分割策略。支持的策略有“best”选择最佳分割和“random”选择最佳随机分割。

• max_depth: 整数或None，可选参数（默认为None）或树的最大深度。树的最大深度。如果为None，则节点会扩展直到所有叶子节点包含的样本数少于min_samples_split。最大深度的值过高会导致过拟合，而过低的值会导致欠拟合。

这里选择max_depth=3，也可以换成其他预修剪

clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
clf = clf.fit(X_train,y_train)
y_pred = clf.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

分类率变成了77.056%，效果可观

2.7 可视化优化模型

from six import StringIO from IPython.display import Image  
from sklearn.tree import export_graphviz
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,  
                filled=True, rounded=True,
                special_characters=True, feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())  
graph.write_png('diabetes.png')
Image(graph.create_png())

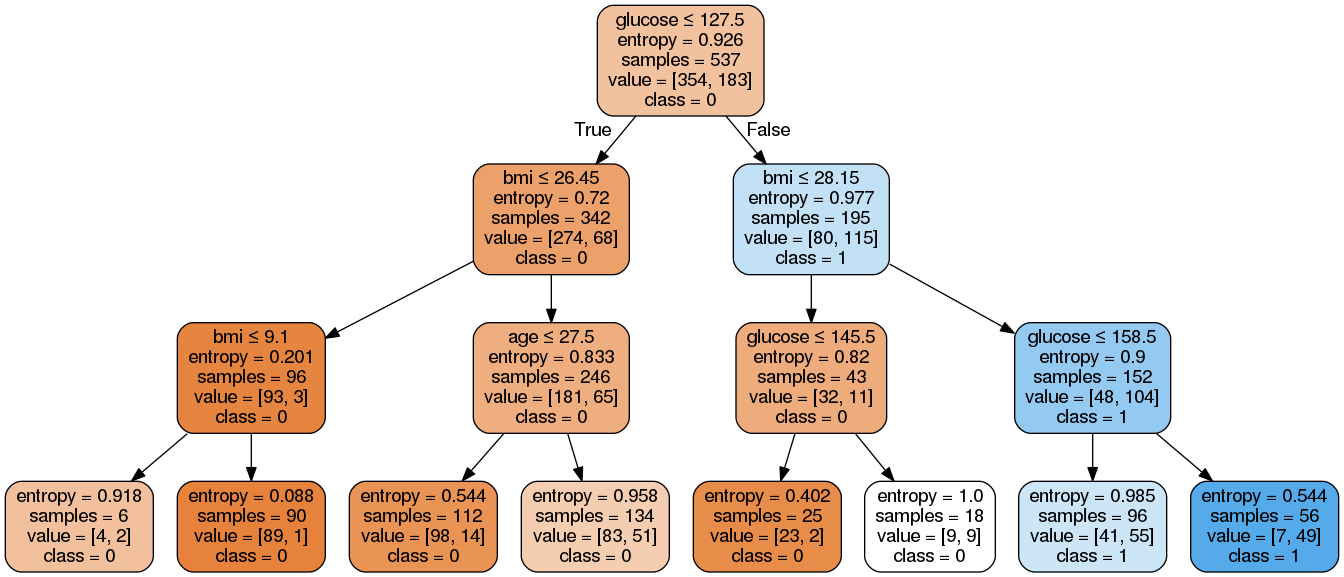
确实结果比优化前的更简洁了，分类后的复杂程度大大降低了。

3 讨论

Python中的决策树是机器学习（数据科学的重要子集）领域非常流行的监督学习算法技术，但是，决策树并不是可用于提取此信息的唯一聚类技术。

它是一种监督式机器学习技术，其中数据根据某个参数连续拆分。决策树分析可以帮助解决分类和回归问题，这里只演示了分类。决策树算法将数据集分解为更小的子集;同时，相关的决策树是逐步开发的。决策树由节点（测试某个属性的值）、边/分支（对应于测试结果并连接到下一个节点或叶）和叶节点（预测结果的终端节点）组成，使其成为一个完整的结构。