好久没更了![]()
写天梯模拟L1都有题不能AC,是什么品种的蒟蒻![]()
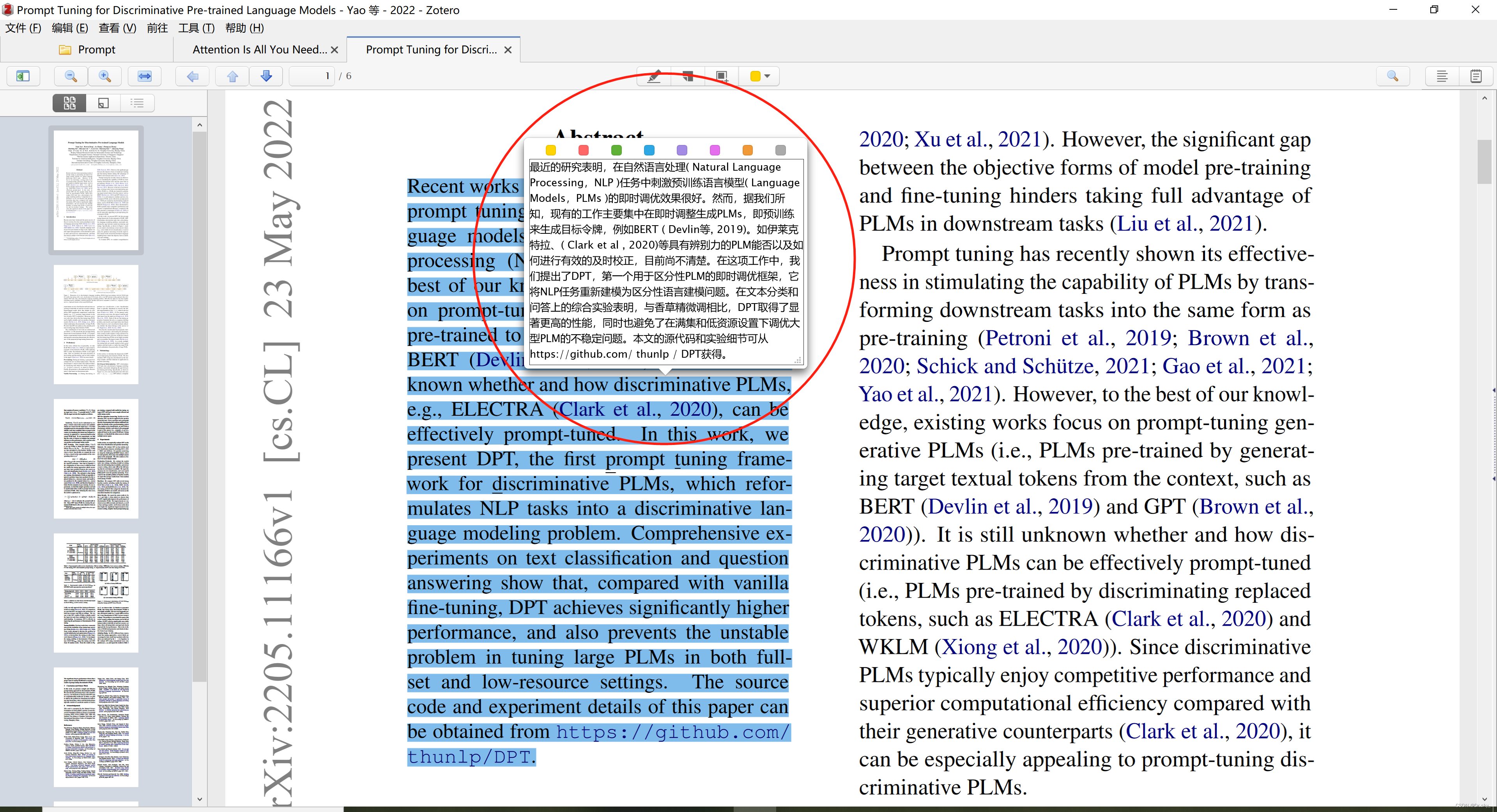
L1-7 谷歌的招聘
题目详情 - L1-7 谷歌的招聘 (pintia.cn)
自己写半天都是Segmentation Fault,
学习一下几个函数叭//
1.substr()函数
获取子串
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s1="1a2b3c4d5e";
string s2=s1.substr(2,5);//表示从s1的下标为2的位置开始取长度为5的字符串
cout<<s2; //2b3c4
return 0;
}2.atoi( )函数
字符串转化为整数
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s1="123456";
long long a=atoi(s1.c_str());//c_str()返回的是一个临时指针
cout<<a;
return 0;
}组合一下就可以AC咯 ![]()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int l,k;
string s;
int isprime(int a)//判断素数
{
if(a==1||a==0) return 0;
for(int i=2;i<sqrt(a);i++)
{
if(a%i==0) return 0;
}
return 1;
}
int main()
{
int i;
cin>>l>>k;
getchar();
getline(cin,s);
for(i=0;i<=l-k;i++)
{
string str=s.substr(i,k);//截取长度为k的字符串
ll temp=atoi(str.c_str());//转化为一个整数
if(isprime(temp))
{
cout<<str;
return 0;
}
}
cout<<"404";
return 0;
} 参考:
2020天梯模拟赛L1-7谷歌的招聘 - Jinx8823 - 博客园 (cnblogs.com)
L1-4 冠军魔术
题目详情 - L1-4 冠军魔术 (pintia.cn)
这题就一数学题,苦恼了很久不能AC的原因,逻辑和公式是没有问题的;
但把n*pow(2,c/2)直接输出就会WA一个点,但是用sum记录再输出就能过???
原因是pow函数的返回值是double![]()
AC:
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,c;
int main()
{
scanf("%d %d",&n,&c);
int sum=n*pow(2,c/2);
if(c%2==0)
{
cout<<"0 "<<sum;
}else{
cout<<"1 "<<sum;
}
return 0;
}
8分:
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
long long n,c;
int main()
{
scanf("%lld%lld",&n,&c);
if(c%2==0)
{
cout<<"0 "<<n*pow(2,c/2);
}else{
cout<<"1 "<<n*pow(2,c/2);
}
return 0;
}
//0 硬币,1 纸牌 P2241 统计方形(数据加强版)
本鼠鼠还是偏爱洛谷的,可以看题解(bushi
P2241 统计方形(数据加强版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
就是熟悉一下公式,免得脑子突然糨糊
正方形个数
边长为1 个数n*m
边长为2 个数(n-1)*(m-1)
边长为3 个数(n-2)*(m-2)
所以 边长为min{n,m} 个数(m-min{n,m}+1)*(n-min{n,m}+1)
长方形加正方形个数
total=(1+2+3+…+n)*(1+2+3+…+m)
=((1+n)*(1+m)*n*m)/4
长方形个数
上面两式相减即可得出
所以思路就是 先算出正方形个数 然后用公式得出长方形和正方形个数总和 最后得到长方形个数
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=15;
int n,m;
int sum;
signed main()
{
cin>>n>>m;
int p=min(n,m);
for(int i=1;i<=p;i++)
{
sum+=(n-i+1)*(m-i+1);
}
cout<<sum<<" "<<m*n*(m+1)*(n+1)/4-sum;
return 0;
}