Python常用练习小例子
1、输出九九乘法表
源码如下:
# 九九乘法表
for i in range(1, 10):
for j in range(1, i+1):
print('{}x{}={}\t'.format(i, j, i*j), end='')
print() # 换行,相当于print(end='\n')其中,rint('{}x{}={}\t'.format(i, j, i*j), end='') 可改为 print ("%dx%d=%d\t" % (i, j, i*j), end='')
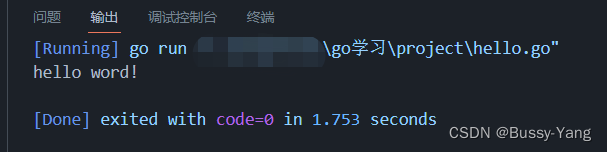
运行效果:
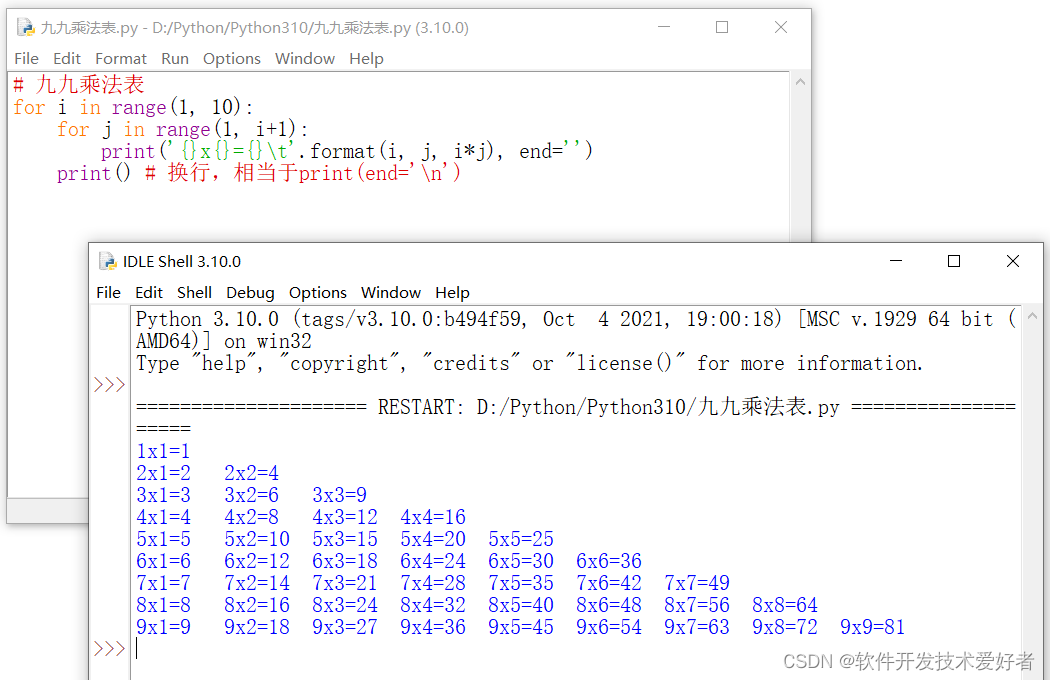
关于Python的输入函数input()和输出函数print() 可参见https://blog.csdn.net/cnds123/article/details/118638607
2、判断用户输入的年份是否为闰年
源码如下:
year = int(input("输入一个年份: "))
if (year % 4) == 0:
if (year % 100) == 0:
if (year % 400) == 0:
print("{0} 是闰年".format(year)) # 整百年能被400整除的是闰年
else:
print("{0} 不是闰年".format(year))
else:
print("{0} 是闰年".format(year)) # 非整百年能被4整除的为闰年
else:
print("{0} 不是闰年".format(year))
3、斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……。
在数学上,费波那契数列是以递归的方法来定义:
F0 = 0 (n=0)
F1 = 1 (n=1)
Fn = F[n-1]+ F[n-2](n=>2) 即从第三项开始,每一项都等于前两项之和。
法一、采用递归
# 获取用户输入数据
nterms = int(input("需要几项?"))
#递归
def fib(n):
if n == 1:
return [1]
if n == 2:
return [1, 1]
fibs = [1, 1]
for i in range(2, n):
fibs.append(fibs[-1] + fibs[-2])
return fibs
# 判断输入的值是否合法
if nterms <= 0:
print("请输入一个正整数。")
else:
print (fib(nterms))
法二、不用递归
# 获取用户输入数据
nterms = int(input("需要几项?"))
#不用递归
#求第n项(n>2)
def fn(n):
a,b = 1,1
for i in range(n-1):
a,b = b,a+b
return a
def fib(n):
if n == 1:
return [1]
if n == 2:
return [1, 1]
fibs = [1, 1]
for i in range(2, n):
fibs.append(fn(nterms))
return fibs
# 判断输入的值是否合法
if nterms <= 0:
print("请输入一个正整数。")
else:
print (fib(nterms))
4、将一个正整数分解质因数
对n进行分解质因数,应先找到一个最小的质数k,然后按下述步骤完成:
(1)如果这个质数恰等于n,则说明分解质因数的过程已经结束,打印出即可。
(2)如果n<>k,但n能被k整除,则应打印出k的值,并用n除以k的商,作为新的正整数你n,重复执行第一步。
(3)如果n不能被k整除,则用k+1作为k的值,重复执行第一步。
程序源代码如下:
# 获取用户输入数据
N = int(input("请输入一个正整数:"))
def reduceNum(n):
print ('{} = '.format(n), end=" ")
if not isinstance(n, int) or n <= 0 :
print ('请输入一个正确的数字 !')
exit(0)
elif n in [1] :
print ('{}'.format(n))
while n not in [1] : # 循环保证递归
for index in range(2, n + 1) :
if n % index == 0:
n //= index # n 等于 n//index
if n == 1:
print (index )
else : # index 一定是素数
print ('{} *'.format(index), end=" ")
break
reduceNum(N)