大白鲨优化算法（WSO）（Matlab代码实现）

news2024/11/26 6:01:14

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

这是一种新颖的元启发式算法，称为白鲨优化优化算法（WSO），用于解决连续搜索空间上的优化问题。WSO的核心思想和基础受到大白鲨行为的启发，包括它们在导航和觅食时非凡的听觉和嗅觉。对行为的这些方面进行了数学建模，以适应WSO的探索和利用之间的充分平衡，并帮助搜索代理探索和利用搜索空间的每个潜在区域以实现优化。WSO的搜索代理随机更新其与迄今为止最佳解决方案相关的位置，以最终得出最佳结果。

📚2 运行结果

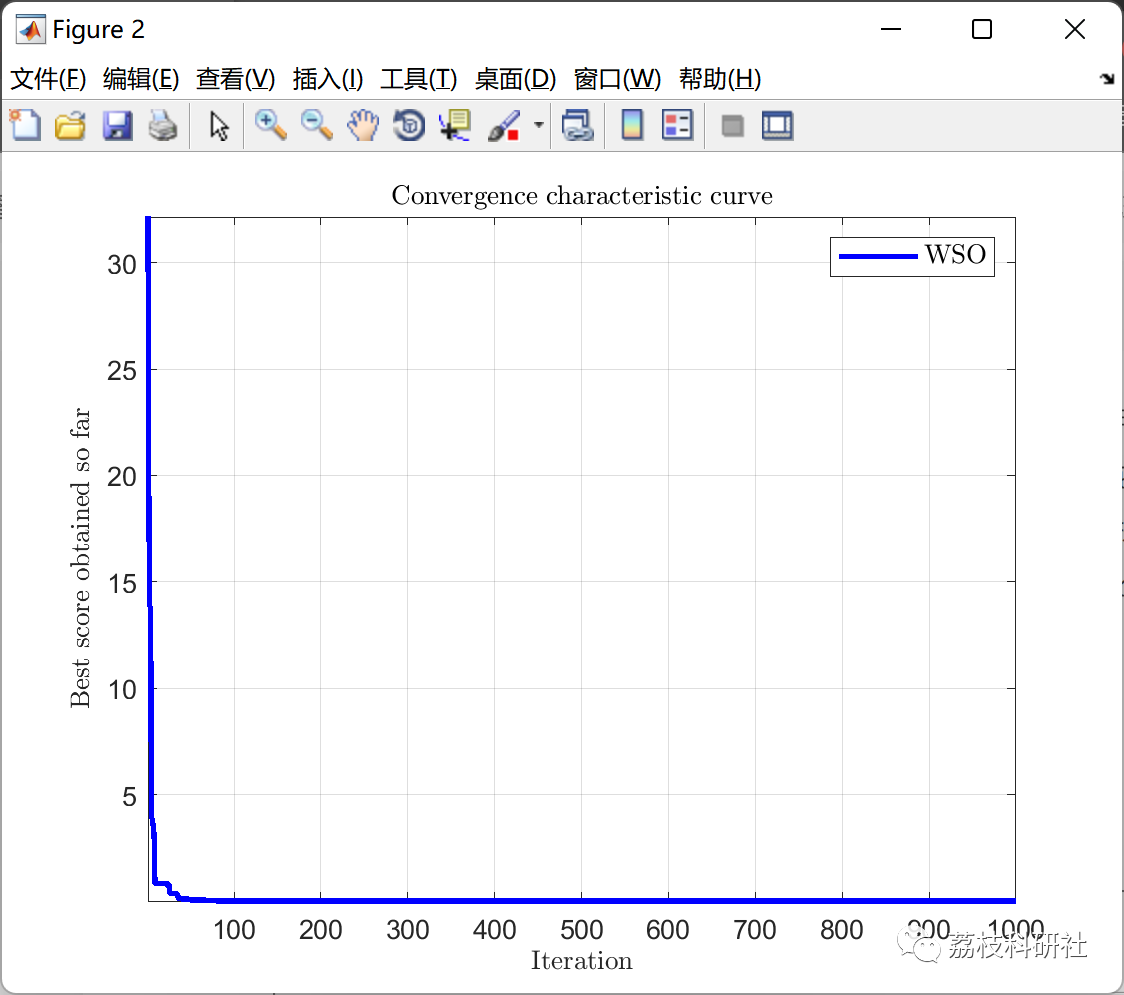
部分代码：

function [fmin0,gbest,ccurve]=WSO(whiteSharks,itemax,lb,ub,dim,fobj)

%% Convergence curve
ccurve=zeros(1,itemax);

%%% Show the convergence curve
figure (1);
set(gcf,'color','w');
hold on
xlabel('Iteration','interpreter','latex','FontName','Times','fontsize',10)
ylabel('fitness value','interpreter','latex','FontName','Times','fontsize',10);
grid;

%% Start the WSO Algorithm
% Generation of initial solutions
WSO_Positions=initialization(whiteSharks,dim,ub,lb);% Initial population

% initial velocity
v=0.0*WSO_Positions;

%% Evaluate the fitness of the initial population
fit=zeros(whiteSharks,1);

for i=1:whiteSharks
fit(i,1)=fobj(WSO_Positions(i,:));
end

%% Initalize the parameters of WSO
fitness=fit; % Initial fitness of the random positions of the WSO

[fmin0,index]=min(fit);

wbest = WSO_Positions; % Best position initialization
gbest = WSO_Positions(index,:); % initial global position

%% WSO Parameters
fmax=0.75; % Maximum frequency of the wavy motion
fmin=0.07; % Minimum frequency of the wavy motion
tau=4.11;

mu=2/abs(2-tau-sqrt(tau^2-4*tau));

pmin=0.5;
pmax=1.5;
a0=6.250;
a1=100;
a2=0.0005;
%% Start the iterative process of WSO
for ite=1:itemax

mv=1/(a0+exp((itemax/2.0-ite)/a1));
s_s=abs((1-exp(-a2*ite/itemax))) ;

p1=pmax+(pmax-pmin)*exp(-(4*ite/itemax)^2);
p2=pmin+(pmax-pmin)*exp(-(4*ite/itemax)^2);

%% Update the speed of the white sharks in water
nu=floor((whiteSharks).*rand(1,whiteSharks))+1;

for i=1:size(WSO_Positions,1)
rmin=1; rmax=3.0;
rr=rmin+rand()*(rmax-rmin);
wr=abs(((2*rand()) - (1*rand()+rand()))/rr);
v(i,:)= mu*v(i,:) + wr *(wbest(nu(i),:)-WSO_Positions(i,:));
%% or

% v(i,:)= mu*(v(i,:)+ p1*(gbest-WSO_Positions(i,:))*rand+....
% + p2*(wbest(nu(i),:)-WSO_Positions(i,:))*rand);
end

%% Update the white shark position
for i=1:size(WSO_Positions,1)

f =fmin+(fmax-fmin)/(fmax+fmin);

a=sign(WSO_Positions(i,:)-ub)>0;
b=sign(WSO_Positions(i,:)-lb)<0;

wo=xor(a,b);

% locate the prey based on its sensing (sound, waves)
if rand<mv
WSO_Positions(i,:)= WSO_Positions(i,:).*(~wo) + (ub.*a+lb.*b); % random allocation
else
WSO_Positions(i,:) = WSO_Positions(i,:)+ v(i,:)/f; % based on the wavy motion
end
end

%% Update the position of white sharks consides_sng fishing school
for i=1:size(WSO_Positions,1)
for j=1:size(WSO_Positions,2)
if rand<s_s

Dist=abs(rand*(gbest(j)-1*WSO_Positions(i,j)));

if(i==1)
WSO_Positions(i,j)=gbest(j)+rand*Dist*sign(rand-0.5);
else
WSO_Pos(i,j)= gbest(j)+rand*Dist*sign(rand-0.5);
WSO_Positions(i,j)=(WSO_Pos(i,j)+WSO_Positions(i-1,j))/2*rand;
end
end

end
end
%

%% Update global, best and new positions

for i=1:whiteSharks
% Handling boundary violations
if WSO_Positions(i,:)>=lb & WSO_Positions(i,:)<=ub%
% Find the fitness
fit(i)=fobj(WSO_Positions(i,:));

% Evaluate the fitness
if fit(i)<fitness(i)
wbest(i,:) = WSO_Positions(i,:); % Update the best positions
fitness(i)=fit(i); % Update the fitness
end

%% Finding out the best positions
if (fitness(i)<fmin0)
fmin0=fitness(i);
gbest = wbest(index,:); % Update the global best positions
end

end
end

%% Obtain the results
outmsg = ['Iteration# ', num2str(ite) , ' Fitness= ' , num2str(fmin0)];
disp(outmsg);

ccurve(ite)=fmin0; % Best found value until iteration ite

if ite>2
line([ite-1 ite], [ccurve(ite-1) ccurve(ite)],'Color','b');
title({'Convergence characteristic curve'},'interpreter','latex','FontName','Times','fontsize',12);
xlabel('Iteration');
ylabel('Best score obtained so far');
drawnow
end

end
end