LeetCode 热题 HOT 100
76. 最小覆盖子串
题目:给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
package ricky.com.Hot100;
/**
* @Author xdg
*/
public class minWindow {
/*
* 76. 最小覆盖子串
* 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
* 注意:
* 对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
* 如果 s 中存在这样的子串,我们保证它是唯一的答案。
*/
class Solution {
public String minWindow(String s, String t) {
if (t == null || t.length() == 0) {
return "";
}
//把t中的每个字符出现的次数统计出来
int[] arr = new int[128];
for (int i = 0; i < t.length(); i++) {
arr[t.charAt(i)]++;
}
int l = 0;
int r = 0;
//记录t中所有字符出现的次数,为0时说明找到一个答案
int total = t.length();
int len = Integer.MAX_VALUE;
//字符串的起始位置
int start = 0;
for (r = 0; r < s.length(); r++) {
//此时s.charAt(r)字符在t串中,total--
if (arr[s.charAt(r)] > 0) {
total--;
}
//arr中t串中对应的字符数量也要减一,但它始终是>=0的,如果字符不在t串中,会减成负数
arr[s.charAt(r)]--;
//找到答案,记录
while (total == 0) {
//因为是最小子串,所以取小值
if (len > r - l + 1) {
//字符串的长度
len = r - l + 1;
//记录起始位置
start = l;
}
//在将字符移出窗口之前,先要加1,不然移出后就晚了
arr[s.charAt(l)]++;
if (arr[s.charAt(l)] > 0) {
total++;
}
//窗口右移一位
l++;
}
}
return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
}
}
}
代码解释:
if (t == null || t.length() == 0) { return ""; }如果
t为空或长度为0,则直接返回空字符串。int[] arr = new int[128]; for (int i = 0; i < t.length(); i++) { arr[t.charAt(i)]++; }定义一个长度为128的整型数组
arr,用于统计字符串t中每个字符出现的次数。遍历字符串t,将arr中对应字符的计数加1。int l = 0; int r = 0; int total = t.length(); int len = Integer.MAX_VALUE; int start = 0;定义五个变量,分别是左指针
l、右指针r、字符串t的长度total、最小子串长度len和最小子串的起始位置start。for (r = 0; r < s.length(); r++) { if (arr[s.charAt(r)] > 0) { total--; } arr[s.charAt(r)]--; while (total == 0){ if (len > r - l + 1){ len = r - l + 1; start = l; } arr[s.charAt(l)]++; if (arr[s.charAt(l)] > 0){ total++; } l++; } }遍历字符串
s,用滑动窗口的方法查找最小子串。当右指针r指向的字符在t中出现时,将total减1;同时将数组arr中对应字符的计数减1。当total等于0时,表示当前窗口包含了t中的所有字符,需要将左指针l向右移动,缩小窗口范围。每次移动左指针l时,需要将数组arr中对应字符的计数加1,如果加1后该字符的计数大于0,则将total加1。此外,还需要更新最小子串的长度和起始位置。return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);返回最小子串,如果
len的值没有被更新过,即没有找到符合要求的子串,则返回空字符串。
84. 柱状图中最大的矩形
题目:给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
**示例 1:
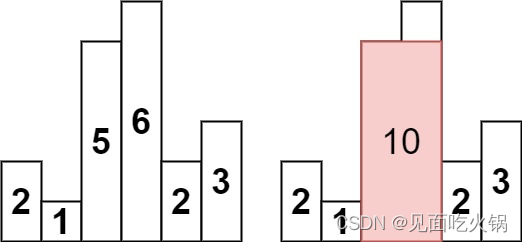
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
package ricky.com.Hot100;
/**
* @Author xdg
*/
public class largestRectangleArea {
/*84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。*/
class Solution {
public int largestRectangleArea(int[] heights) {
// 定义两个数组,分别用来存储当前柱子左边第一个小于其高度的柱子的下标和右边第一个小于其高度的柱子的下标
int[] leftMin = new int[heights.length];
int[] rightMin = new int[heights.length];
// 初始化左边第一个小于其高度的柱子的下标,第一个柱子左边没有小于其高度的柱子
leftMin[0] = -1;
// 初始化右边第一个小于其高度的柱子的下标,最后一个柱子右边没有小于其高度的柱子
rightMin[heights.length - 1] = heights.length;
// 遍历所有柱子,计算左边第一个小于其高度的柱子的下标
for (int i = 1; i < heights.length; i++) {
int temp = i - 1;
// 如果当前柱子的高度大于等于左边某个柱子的高度,则将左边柱子的左边第一个小于其高度的柱子的下标作为当前柱子的左边第一个小于其高度的柱子的下标
while (temp >= 0 && heights[temp] >= heights[i]) {
temp = leftMin[temp];
}
leftMin[i] = temp;
}
// 遍历所有柱子,计算右边第一个小于其高度的柱子的下标
for (int i = heights.length - 2; i >= 0; i--) {
int temp = i + 1;
// 如果当前柱子的高度大于等于右边某个柱子的高度,则将右边柱子的右边第一个小于其高度的柱子的下标作为当前柱子的右边第一个小于其高度的柱子的下标
while (temp < heights.length && heights[temp] >= heights[i]) {
temp = rightMin[temp];
}
rightMin[i] = temp;
}
// 遍历所有柱子,计算能够勾勒出来的矩形的最大面积
int res = 0;
for (int i = 0; i < heights.length; i++) {
// 当前柱子的高度乘以左边第一个小于其高度的柱子和右边第一个小于其高度的柱子之间的距离就是当前能够勾勒出来的矩形的面积
res = Math.max(res, heights[i] * (rightMin[i] - leftMin[i] - 1));
}
// 返回最大面积
return res;
}
}
}
96. 不同的二叉搜索树
题目:给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?
返回满足题意的二叉搜索树的种数。
**示例 1:
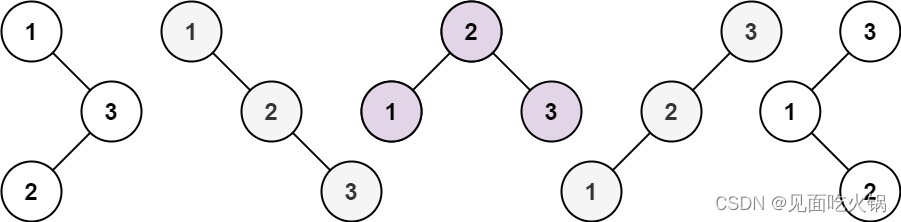
输入:n = 3
输出:5
思路分析: 使用一个一维数组 dp 来记录每个节点数能够构成的二叉搜索树的个数。在遍历每个节点数的过程中,枚举左子树节点数 j 和右子树节点数 i-1-j,然后将左右子树能够构成的所有情况之和累加到 dp[i] 中,最终返回 dp[n] 即可。
package ricky.com.Hot100;
/**
* @Author xdg
*/
class Solution {
public int numTrees(int n) {
// 如果输入 n 为 0,返回 0
if (n == 0) {
return 0;
}
// 定义数组 dp,dp[i] 表示 i 个节点能够构成的二叉搜索树的个数
int[] dp = new int[n + 1];
// 初始化 dp[0] 为 1,表示空树也算一种二叉搜索树
dp[0] = 1;
// 遍历每个节点数量,从 1 到 n
for (int i = 1; i <= n; i++) {
// 遍历左子树节点数量 j,从 0 到 i-1
for (int j = 0; j < i; j++) {
// dp[j] 表示左子树能够构成的二叉搜索树的个数
// dp[i - 1 - j] 表示右子树能够构成的二叉搜索树的个数
// 二者相乘即为以 j 为根节点,左子树有 dp[j] 种情况,右子树有 dp[i - 1 - j] 种情况的所有情况之和
dp[i] += dp[j] * dp[i - 1 - j];
}
}
// 返回 dp[n],即 n 个节点能够构成的二叉搜索树的个数
return dp[n];
}
}