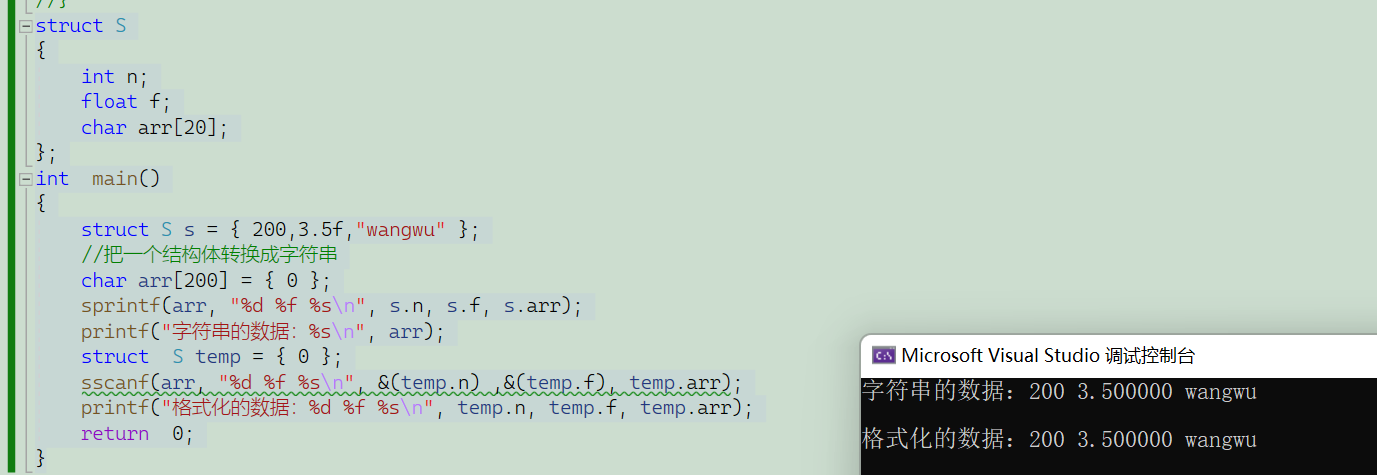
深度学习中经常要对概率密度建模。对于多维度随机变量来说，这有些困难。概率化结构（既图模型）是处理这个问题的手段之一。这引出了两个问题。为什么建模困难？图模型怎样解决了这个困难？

关于这个问题，花书给出了回答。关于图模型解释主要是围绕展开可以降低参数量展开。很多博客也对此进行了回答，但我对那些回答并不满意。这些博客多是摘取了书中的几句话，也不说清楚参数多在哪里。在我看来，发这样的笔记，不如保存本地不要发布。

结构化数据

很多随机变量之间是有相互关系的，比如图片生成。相邻的两个像素之间关联很大。对于一张3232的黑白图片，我们想要表示概率密度函数，就需要表示3232*2种情况，也就是$32\ast 32\ast 2个$参数。也就是每一个情况的概率值，都用一个参数表示。我们知道，所有情况概率和为1，所以知道$32\ast 32\ast 2-1个$参数即可。这时候如果考虑了随机变量之间的关联性是怎样的，便可以减少表示所用的参数，简化问题。

贝叶斯网络如何减少参数？

拿我自己博客的例子：

• 谈到毕业生的薪水时，我们很感兴趣的两个随机变量是$X_1$为哪个学校毕业，$X_2$为薪水多少。在这个随机试验里，$P(X_2=高薪|X_1=清华大学)>P(X_2=高薪|X_1=10422)$。
• 对于身高，以父母身高为$X_1和X_2$,孩子身高为$X_3$，成长省份为$X_4$，苹果手机今年的发布价格为$X_5$，苹果手机的销量为$X_6$。在这个随机试验里，$P(X_1=1.7,X_2=1.7,X_3=1.7,X_4=湖南,X_5=9k)=P(X_1=1.7,X_2=1.7,X_3=1.7,X_4=湖南)$。很明显苹果手机的价格和身高这几个随机变量无关。

随机变量之间存在着复杂的关系。从上面的例子看出，我们研究的部分随机变量存在关联，有些不存在关联。直接求解联合概率分布显然是非常复杂的。当我们知道各个随机变量之间的依赖关系时，便可以通过概率图模型降低求解联合分布的难度。随机变量间是有向、无环关系的时候，这种概率图结构就是贝叶斯网络。（无向时为马尔可夫随机场，另一种概率图）

对一个学生能否拿到的薪水进行建模。假设相关的随机变量有5个$X_1$~$X_5$分别是
高考成绩、学校招生人数、就读大学、大学成绩、薪水。
我们关心的是随机变量间的关系，直接用一张图表示出来

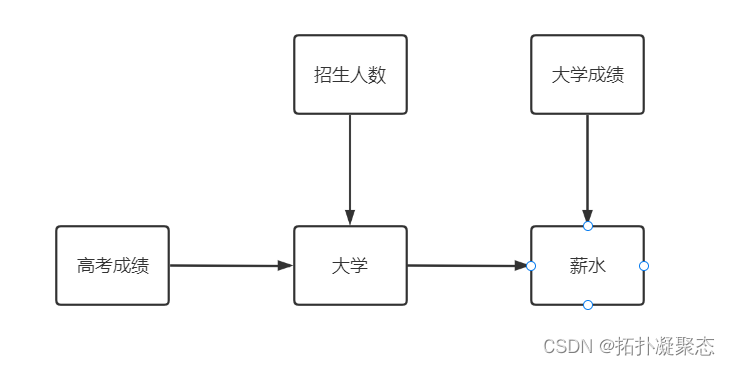
显然从图中可以看出各个变量的依赖关系。这张图体现了2个要素：有向、无环。距离一个完整的贝叶斯网络只差一部，那便是求出多维随机变量的分布。
要求分别，那先明确各个变量的取值（或者说给图的节点定义）：

• 高考成绩$X_1$：高分、低分
• 招生人数$X_2$：多、中、少
• 入读大学$X_3$：清华大学、北京城市学院
• 大学成绩$X_4$：高分、普通、低分
• 薪水$X_5$：高薪、低薪

问题介绍完了。如果直接建模需要多少参数？

$$2\ast 3\ast 2\ast 3\ast 2=72$$
也就是说我们需要表示出：

$P(X_1=高分,X_2=多,X_3=清华大学,X_4=高分,X_5=高薪)={\theta }_1$
$P(X_1=低分,X_2=多,X_3=清华大学,X_4=高分,X_5=高薪)={\theta }_2$
$P(X_1=高分,X_2=中,X_3=清华大学,X_4=高分,X_5=高薪)={\theta }_3$
$...$
一直遍历所有情况。右边的$\theta$便是这种模型表示下的参数。

如果用了贝叶斯网络，那么概率密度可以表示成如下的形式：

$P(X_1,X_2,X_3,X_4,X_5)=P(X_1)P(X_2)P(X_3|X_1,X_2)P(X_4)P(X_5|X_3,X_4)$

这意味着:1.我们只需要分别表示出各项，再通过计算，得出联合概率密度。
2.每个单独的一项，又可以用概率合为1的规定。
这两条极大的减少了我们需要表示的情况。

$P(X_1=高分)={\theta }_1$
$P(X_1=低分)=1-{\theta }_1$

$P(X_2=多)={\theta }_2$
$P(X_2=中)={\theta }_3$
$P(X_3=少)=1-{\theta }_2-{\theta }_3$

$X_1需要1个，X_2需要1个，X_3需要4个,X_4需要3个,X_5需要6个。总共是15个$
可以看出，这样的做法确实降低了模型的参数量。通过这样的方式，我们依然可以得到所有情况，也就是72种情况各自对应的概率。先计算出各个分项的参数，随后通过乘积的方式计算出那个想要表示的联合概率。