算法——双指针技巧总结
- 一、双指针
- 二、链表快慢指针
- 19.删除链表的倒数第 N 个结点
- 双指针
- 206.反转链表
- 思路:
- 双指针法
- 递归法
- 92.反转链表 II
- 1.递归
- 2.迭代(双指针头插法)
- 876.链表的中间结点
- 常规思路
- 双指针思路
- 141.环形链表(判断链表是否有环)
- 双指针
- 142.环形链表 II(找链表的环入口)
- 双指针
- 相交链表
- 思路1
- 思路2
- 三、数组快慢指针
- 27.移除元素
- 1.暴力解法
- 2.双指针法(快慢指针法)
- 3.双指针优化
- 26.删除有序数组中的重复项
- 双指针法
- 80.删除有序数组中的重复项 II
- 1.双指针法
- 2.有序数组去重保留k位重复数的通法
- 283.移动零
- 双指针法
- 四、左右指针
- 977.有序数组的平方
- 1.暴力排序解法
- 2.双指针法(左右指针法)
- 344. 反转字符串 (数组)
- 双指针
- 18. 四数之和
- 双指针法
- 167. 两数之和 II - 输入有序数组
- 870. 优势洗牌
- 回文子串问题
- 五、二分查找与滑动窗口
一、双指针
双指针技巧可细分分为两类,一类是快慢指针,一类是左右指针。
前者解决主要解决链表中的问题,比如典型的判定链表中是否包含环、反转链表、找链表的中间节点、删除链表的倒数第 N 个结点;也用来解决数组中的问题,如移动/移除元素、删除有序数组中的重复项。
后者主要解决数组(或者字符串)中的问题,比如二分查找,滑动窗口。
二、链表快慢指针
快慢指针一般都初始化指向链表的头结点 head,前进时快指针 fast 在前,慢指针 slow 在后,可以巧妙解决一些链表中的问题。
19.删除链表的倒数第 N 个结点
19.删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶:你能尝试使用一趟扫描实现吗?
示例 1:
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1 输出:[]
示例 3:
输入:head = [1,2], n = 1 输出:[1]
双指针
双指针的经典应用,如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了。
定义fast指针和slow指针,初始值为虚拟头结点,如图:
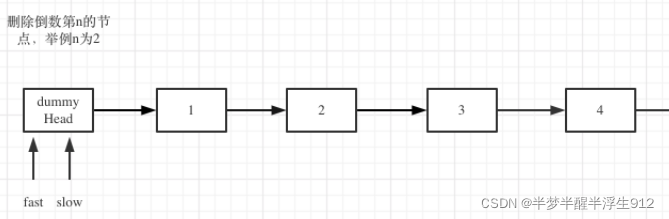
fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
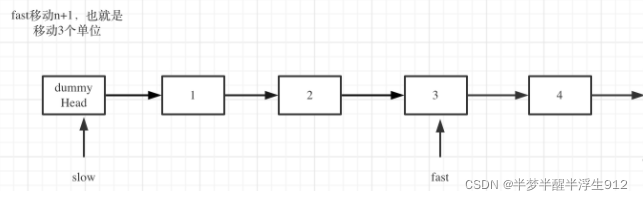
fast和slow同时移动,直到fast指向末尾,如题:
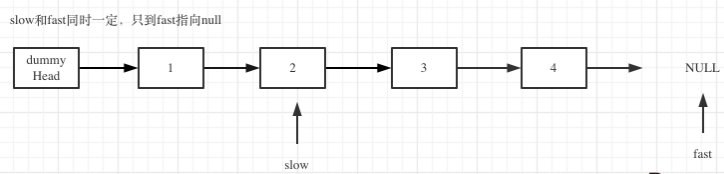
删除slow指向的下一个节点,如图:
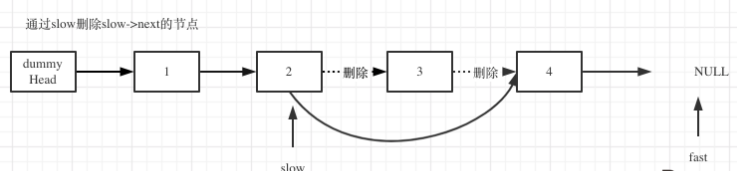
时间复杂度:
O
(
n
)
O(n)
O(n) ,n是链表的长度
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode fast = dummyHead,slow = dummyHead;
while (n--!=0) {
fast = fast.next;
}
fast = fast.next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点
while(fast!=null) {
fast = fast.next;
slow = slow.next;
}
slow.next = slow.next.next;//删除操作
return dummyHead.next;
}
}
206.反转链表
206.反转链表
反转一个单链表。
示例: 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL
思路:
如果再定义一个新的链表,实现链表元素的反转,其实这是对内存空间的浪费。
其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:

定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
然后就要开始反转了,首先要把 cur->next 节点用temp指针保存,因为接下来要改变 cur->next 的指向了,将cur->next 指向pre ,此时已经反转了第一个节点了。
继续移动pre和cur指针。最后,cur 指针已经指向了null,循环结束,链表也反转完毕了。 此时return pre指针就可以了,pre指针就指向了新的头结点。
双指针法
时间复杂度: O ( n ) O(n) O(n) ,n是链表的长度
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode cur = head;
while (cur!=null) {
ListNode temp = cur.next;
cur.next = pre;//反转操作
pre = cur;//更新pre和cur
cur = temp;
}
return pre;
}
}
递归法
时间复杂度:
O
(
n
)
O(n)
O(n) ,n是链表的长度
空间复杂度:
O
(
n
)
O(n)
O(n)
从前往后翻转指针指向:
class Solution {
public ListNode reverse(ListNode pre,ListNode cur) {
if (cur == null) return pre;
ListNode temp = cur.next;
cur.next = pre;
//如下递归的写法,其实就是做了这两步
// pre = cur;
// cur = temp;
return reverse(cur,temp);
}
public ListNode reverseList(ListNode head) {
//初始化pre=null,cur=head
return reverse(null,head);
}
}
上面的递归写法和双指针法实质上都是从前往后翻转指针指向,还有另外一种与双指针法不同思路的递归写法:从后往前翻转指针指向
class Solution {
public ListNode reverseList(ListNode head) {
// 边缘条件判断 base case
if (head == null) return null;
if (head.next == null) return head;
// 递归调用,翻转第二个节点开始往后的链表
ListNode last = reverseList(head.next);
// 翻转头节点与第二个节点的指向
head.next.next = head;
// 此时的 head 节点为尾节点,next 需要指向 NULL
head.next = null;
return last;
}
}
92.反转链表 II
92.反转链表 II
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回反转后的链表 。
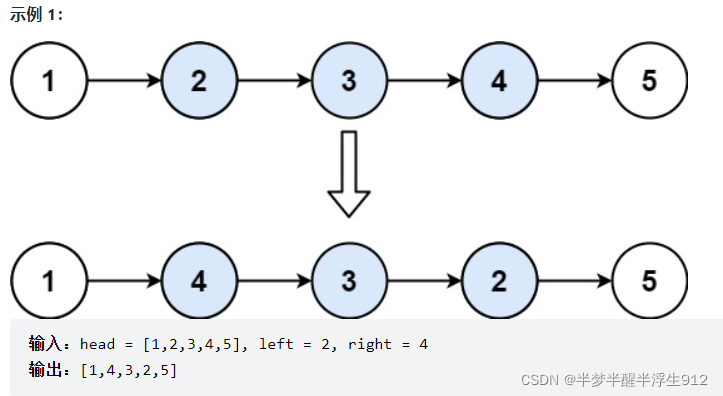
1.递归
先实现反转链表前 n 个节点:
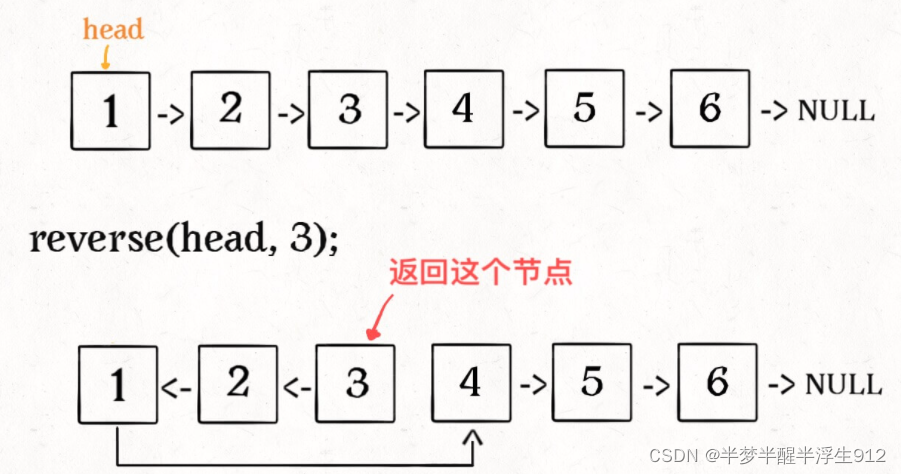
ListNode successor = null; // 后驱节点
// 反转以 head 为起点的 n 个节点,返回新的头结点
ListNode reverseN(ListNode head, int n) {
if (n == 1) {
// 记录第 n + 1 个节点
successor = head.next;
return head;
}
// 以 head.next 为起点,需要反转前 n - 1 个节点
ListNode last = reverseN(head.next, n - 1);
//反转指针
head.next.next = head;
// 让反转之后的 head 节点和后面的节点连起来
head.next = successor;
return last;
}
与完全反转的区别:
- base case 变为 n == 1,反转一个元素,就是它本身,同时要记录后驱节点。
- 直接把 head.next 设置为 null,因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 successor(第 n + 1 个节点),反转之后将 head 连接上。
递归反转链表的一部分:
给一个索引区间 [m,n](索引从 1 开始),仅仅反转区间中的链表元素
ListNode reverseBetween(ListNode head, int m, int n) {
// base case
if (m == 1) {
return reverseN(head, n);
}
// 前进到反转的起点触发 base case
head.next = reverseBetween(head.next, m - 1, n - 1);
return head;
}
2.迭代(双指针头插法)
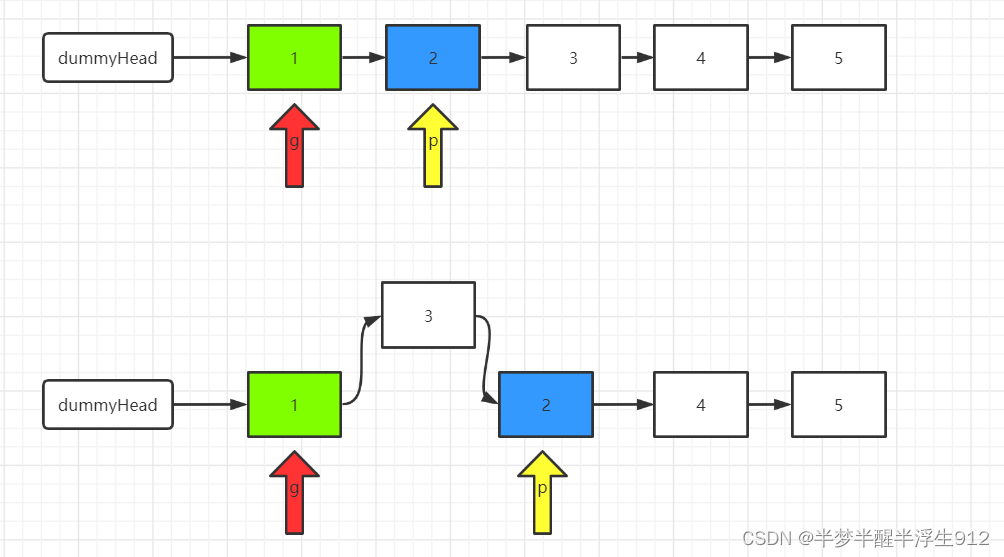
- 定义两个指针,分别称之为 g(guard 守卫) 和 p(point)。
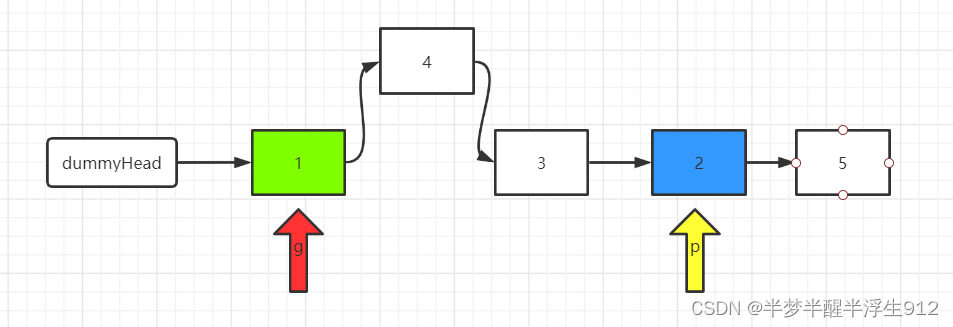
根据参数 m 确定 g 和 p 的位置。将 g 移动到第一个要反转的节点的前面,将 p 移动到第一个要反转的节点的位置上。以 m=2,n=4为例。 - 将 p 后面的元素删除,然后添加到 g 的后面。即头插法。
- 根据 m 和 n 重复步骤(2)
- 返回 dummyHead.next
class Solution {
public ListNode reverseBetween(ListNode head, int m, int n) {
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
// 初始化指针
ListNode g = dummyHead;
ListNode p = dummyHead.next;
// 将指针移到相应的位置
for(int i = 0; i < m - 1; i++) {
g = g.next; p = p.next;
}
// 头插法插入节点
for (int j = 0; j < n - m; j++) {
ListNode removed = p.next;
p.next = p.next.next;
removed.next = g.next;
g.next = removed;
}
return dummyHead.next;
}
}
876.链表的中间结点
876.链表的中间结点
给定一个头结点为 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
常规思路
无法直接得到单链表的长度 n,常规方法就是先遍历链表计算 n,再遍历一次得到第 n / 2 个节点,也就是中间节点。
双指针思路
让两个指针 slow 和 fast 分别指向链表头结点 head。
每当慢指针 slow 前进一步,快指针 fast 就前进两步,这样,当 fast 走到链表末尾时,slow 就指向了链表中点。
class Solution {
public ListNode middleNode(ListNode head) {
ListNode slow = head,fast = head;
while(fast!=null&&fast.next!=null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
}
141.环形链表(判断链表是否有环)
141.环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
双指针
每当慢指针 slow 前进一步,快指针 fast 就前进两步。
如果 fast 最终遇到空指针,说明链表中没有环;如果 fast 最终和 slow 相遇,那肯定是 fast 超过了 slow 一圈,说明链表中含有环。
public class Solution {
public boolean hasCycle(ListNode head) {
ListNode slow = head,fast = head;
while(fast!=null && fast.next!=null) {
slow = slow.next;
fast = fast.next.next;
if (slow==fast) {
return true;
}
}
return false;
}
}
142.环形链表 II(找链表的环入口)
leetcode 142.环形链表 II
题意: 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
双指针
- 判断链表是否有环
- 如果有环,找链表的环入口
假设从头结点到环形入口节点的节点数为x。 环形入口节点到 fast 指针与slow指针相遇节点节点数为y。 从相遇节点再到环形入口节点节点数为 z。 如图所示:
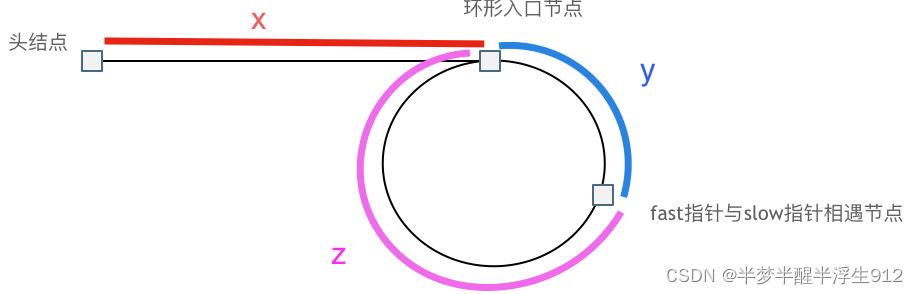
相遇时: slow指针走过的节点数为: x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针,(y+z)为 一圈内节点的个数A。
因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2,化简得x + y = n (y + z)
因为要找环形的入口,那么要求的是x(头结点到环形入口节点的的距离)
x = n (y + z) - y
再从n(y+z)中提出一个(y+z)来,整理公式之后为如下公式:
x = (n - 1) (y + z) + z
注意这里n一定是大于等于1的,因为 fast指针至少要多走一圈才能相遇slow指针。
当 n为1的时候,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了,公式就化解为 x = z
结论:从头结点出发一个指针,从相遇节点也出发一个指针,这两个指针每次只走一个节点,那么当这两个指针相遇的时候就是环形入口的节点
n如果大于1,就是fast指针在环形转n圈之后才遇到 slow指针。这种情况和n为1的时候效果是一样的,一样可以通过这个方法找到环形的入口节点,只不过,index1 指针在环里多转了(n-1)圈,然后再遇到index2,相遇点依然是环形的入口节点。

public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow = head,fast = head;
while (fast!=null&&fast.next!=null) {
slow = slow.next;
fast = fast.next.next;
if (fast==slow) break;
}
//fast遇空指针,说明无环
if(fast==null||fast.next==null) {
return null;
}
slow = head;
while (slow!=fast) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
相交链表
160.相交链表
面试题 02.07.链表相交
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交:
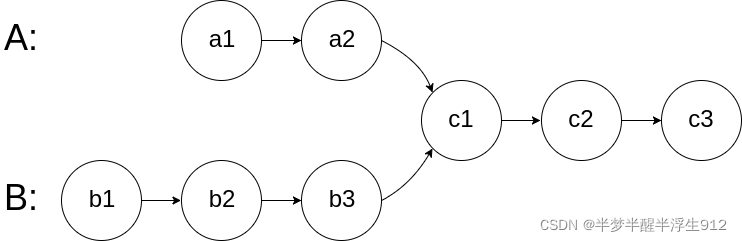
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
示例 1:
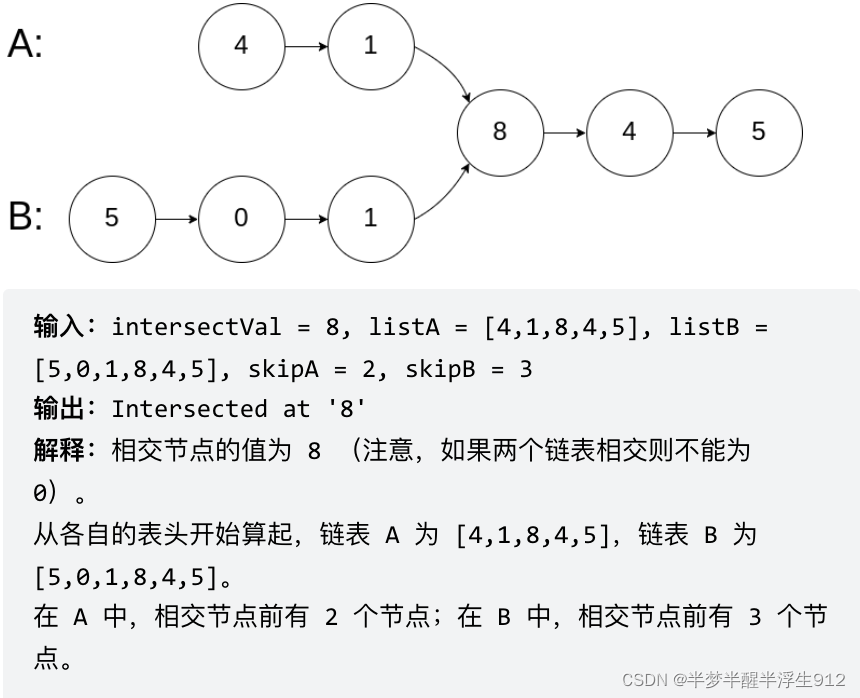
求两个链表交点节点的指针。 交点不是数值相等,而是指针相等。(引用完全相同,即:内存地址完全相同的交点)
难点在于,由于两条链表的长度可能不同,两条链表之间的节点无法对应
如果用两个指针 p1 和 p2 分别在两条链表上前进,并不能同时走到公共节点,也就无法得到相交节点 c1。
解决这个问题的关键是,通过某些方式,让 p1 和 p2 能够同时到达相交节点 c1。
思路1
因为链表自交点后都相等,所以如果有交点则有公共尾部
所以求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置
此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点。否则循环退出返回空指针。
时间复杂度: O ( m + n ) O(m + n) O(m+n),m,n分别为两链表长度
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode curA = headA;
ListNode curB = headB;
int lenA = 0,lenB = 0;
while(curA!=null) {// 求链表A的长度
lenA++;
curA = curA.next;
}
while(curB!=null) {// 求链表B的长度
lenB++;
curB = curB.next;
}
curA = headA;//求长度时改变了curA,curB
curB = headB;//此时要重新改回
// 保证curA为最长链表的头,lenA为其长度
if (lenB > lenA) {
int temp = lenA;
lenA = lenB;
lenB = temp;
ListNode tmp = curA;
curA = curB;
curB = tmp;
}
int sub = lenA - lenB;// 求长度差
// 让curA和curB在同一起点上(末尾位置对齐)
while (sub-- > 0) {
curA = curA.next;
}
// 遍历curA 和 curB,遇到相同则直接返回
while (curA!=null) {
if (curA==curB) {
return curA;
}
curA = curA.next;
curB = curB.next;
}
return null;
}
}
思路2
当链表 headA 和 headB 都不为空时,创建两个指针pA 和 pB,初始时分别指向两个链表的头节点 headA 和headB,然后将两个指针依次遍历两个链表的每个节点。这样相当于逻辑上两条链表接在了一起,就可以让 pA 和 pB 同时到达相交节点 c1。
情况一:两个链表相交
链表headA 和headB 的长度分别是 m 和 n。假设链表headA 的不相交部分有 a 个节点,链表headB 的不相交部分有 b 个节点,两个链表相交的部分有 c 个节点,则有 a+c=m,b+c=n。
-
如果 a=b,则两个指针会同时到达两个链表相交的节点,此时返回相交的节点;
-
如果 a!=b,则指针 pA 会遍历完链表 headA,指针 pB 会遍历完链表 headB,两个指针不会同时到达链表的尾节点,然后指针 pA 移到链表 headB 的头节点,指针 pB 移到链表 headA 的头节点,然后两个指针继续移动,在指针 pA 移动了 a+c+b 次、指针pB 移动了 b+c+a 次之后,两个指针会同时到达两个链表相交的节点,该节点也是两个指针第一次同时指向的节点,此时返回相交的节点。
情况二:两个链表不相交
链表 headA 和headB 的长度分别是 m 和 n。
-
如果 m=n,则两个指针会同时到达两个链表的尾节点,然后同时变成空值 null,此时返回 null;
-
如果m!=n,则由于两个链表没有公共节点,两个指针也不会同时到达两个链表的尾节点,因此两个指针都会遍历完两个链表,在指针 pA 移动了 m+n 次、指针 pB 移动了n+m 次之后,两个指针会同时变成空值null,此时返回 null。
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode pA = headA, pB = headB;
while (pA != pB) {
pA = pA == null ? headB : pA.next;
pB = pB == null ? headA : pB.next;
}
return pA;
}
}
PS:如果把两条链表首尾相连,那么「寻找两条链表的交点」的问题就转换成了前面的「寻找环起点」的问题
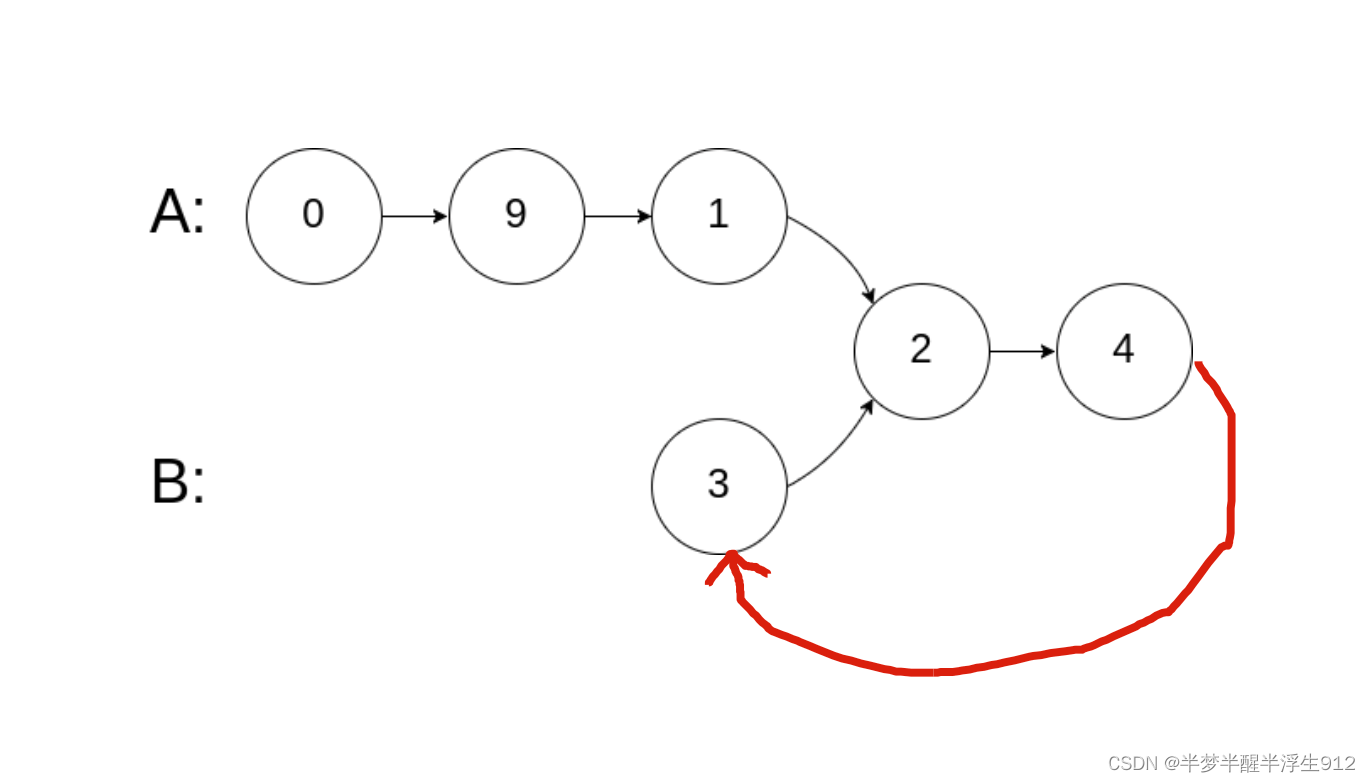
三、数组快慢指针
27.移除元素
27.移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O ( 1 ) O(1) O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
你不需要考虑数组中超出新长度后面的元素。
1.暴力解法
两层for循环,一个for循环遍历数组元素 ,找到需要移除的元素;第二个for循环更新数组,让目标元素以后的数值都向前移动一位,覆盖目标移除的元素。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
class Solution {
public int removeElement(int[] nums, int val) {
int size = nums.length;
for (int i=0;i<size;i++) {
if (nums[i]==val) { // 发现需要移除的元素,就将数组集体向前移动一位
for (int j=i;j<size-1;j++) {
nums[j] = nums[j+1];
}
i--; // 下标i以后的数值都向前移动了一位,所以i也向前移动一位
size--;
}
}
return size;
}
}
2.双指针法(快慢指针法)
通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
双指针法(快慢指针法) 在数组和链表的操作中非常常见,经常用于考察数组、链表、字符串
定义快慢两个指针,快指针指向当前将要处理的元素,慢指针指向下一个将要赋值的位置。在遇到目标值前,快慢指针相等,共同前移遍历;遇到目标值,快指针继续自增,慢指针停留,在之后将快指针指向的值赋给慢指针指向的值,实现覆盖目标值,整个数组前移。遍历完成后,慢指针最后停留的位置即是数组末尾的位置,即数组现在的长度。nums[0…slow] 就是不重复元素。

(图片来自代码随想录)
时间复杂度:
O
(
n
)
O(n)
O(n)
在最坏情况下(输入数组中没有元素等于val),左右指针各遍历了数组一次。需要遍历该序列至多两次
class Solution {
public int removeElement(int[] nums, int val) {
int slowIndex = 0;
for (int fastIndex=0;fastIndex<nums.length;fastIndex++) {
if (nums[fastIndex] != val) {//不等于 \textit{val}val,它一定是输出数组的一个元素
nums[slowIndex] = nums[fastIndex];//将右指针指向的元素复制到左指针位置
slowIndex++; //将左右指针同时右移
}
//等于val,不能在输出数组里,此时左指针不动,右指针右移一位
}
return slowIndex;
}
}
3.双指针优化
如果要移除的元素恰好在数组的开头,例如序列 [1,2,3,4,5],当 val 为1时,我们需要把每一个元素都左移一位。题目中要求要原地移除,但元素的顺序可以改变。实际上我们可以直接将最后一个元素 5 移动到序列开头,取代元素 1,得到序列 [5,2,3,4],同样满足题目要求。这个优化在序列中val元素的数量较少时非常有效。
使用双指针,两个指针初始时分别位于数组的首尾,向中间移动遍历该序列。
如果左指针left 指向的元素等于val,此时将右指针right 指向的元素复制到左指针left 的位置,然后右指针right 左移一位。如果赋值过来的元素恰好也等于val,可以继续把右指针right 指向的元素的值赋值过来(左指针 left 指向的等于val 的元素的位置继续被覆盖),直到左指针指向的元素的值不等于val 为止。
当左指针 left 和右指针right 重合的时候,左右指针遍历完数组中所有的元素。此时数组前半段是有效部分,存储的是不等于 val 的元素;后半段(末尾部分)是无效部分,存储的是等于 val 的元素。
这样的方法两个指针在最坏的情况下合起来只遍历了数组一次。避免了需要保留的元素的重复赋值操作。
时间复杂度:
O
(
n
)
O(n)
O(n)
只需要遍历该序列至多一次。
class Solution {
public int removeElement(int[] nums, int val) {
int left = 0;
int right = nums.length;
while (left < right) {
if (nums[left] == val) {
nums[left] = nums[right - 1];
right--;
} else {
left++;
}
}
return left;
}
}
26.删除有序数组中的重复项
26.删除有序数组中的重复项
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
时间复杂度: O ( n ) O(n) O(n)
双指针法
class Solution {
public int removeDuplicates(int[] nums) {
int slow = 0;
for (int fast=0;fast<nums.length;fast++) {
if (nums[fast]!=nums[slow]) {
slow++; //先自增slow
nums[slow] = nums[fast]; //再赋值
}
}
return slow + 1; //实际数组区间[0,slow],长度slow+1
}
}
或单独讨论数组长度为0的情况,指针从1取起
class Solution {
public int removeDuplicates(int[] nums) {
int n = nums.length;
if (n == 0) {
return 0;
}
int fast = 1, slow = 1;
while (fast < n) {
if (nums[fast] != nums[fast - 1]) {
nums[slow] = nums[fast]; //先赋值
++slow; //再自增slow
}
++fast;
}
return slow; //[0,slow-1],长度slow
}
}
80.删除有序数组中的重复项 II
80.删除有序数组中的重复项 II
1.双指针法
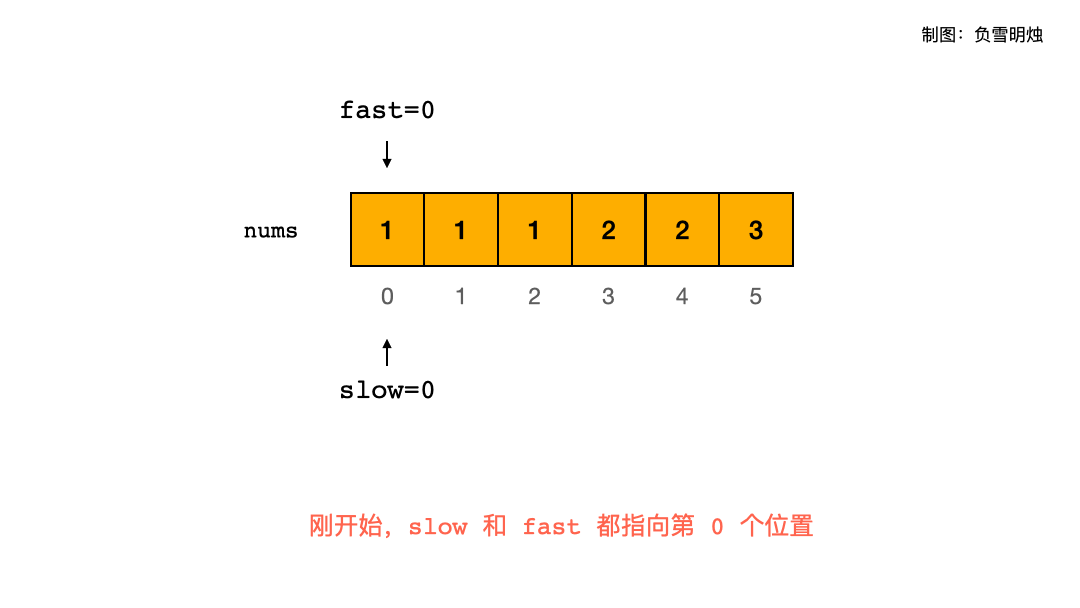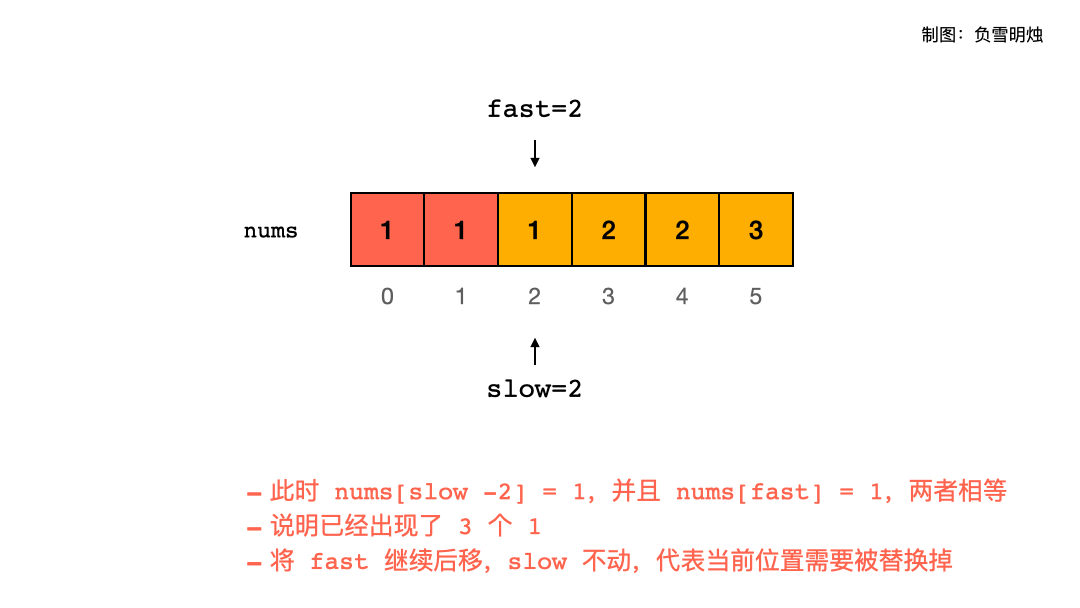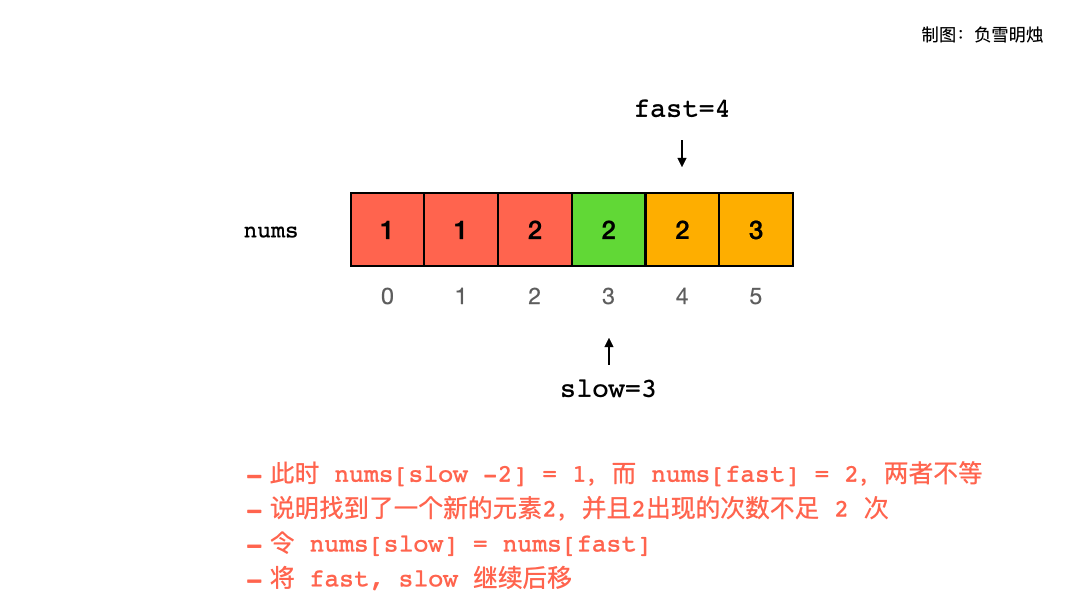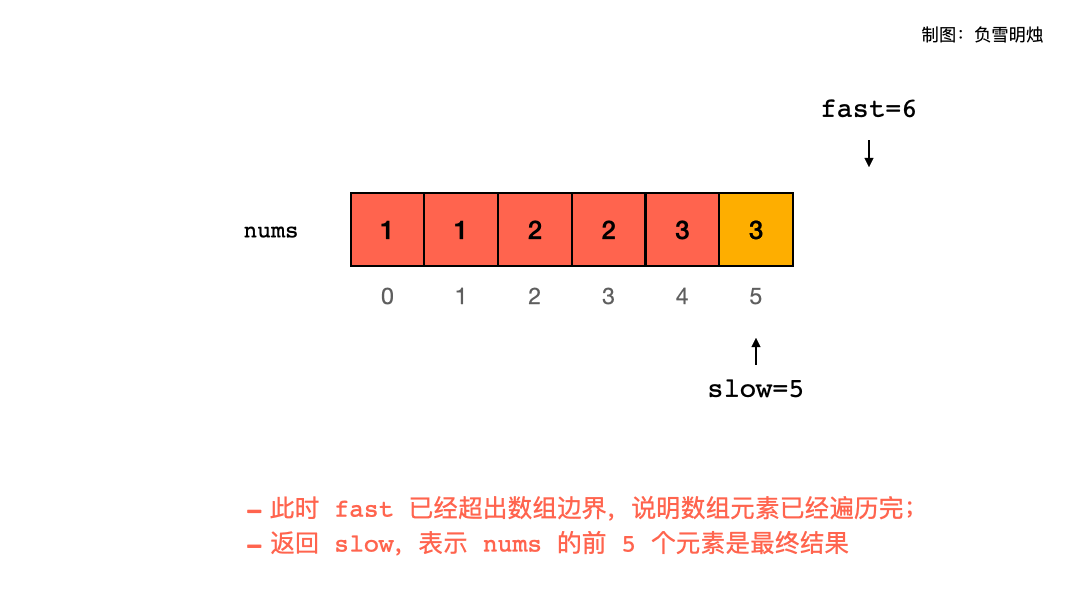
因为本题要求相同元素最多出现两次而非一次,所以我们需要检查上上个应该被保留的元素nums[slow−2] 是否和当前待检查元素nums[fast] 相同。当且仅当nums[slow−2]=nums[fast] 时,当前待检查元素 nums[fast] 不应该被保留(因为此时必然有nums[slow−2]=nums[slow−1]=nums[fast])。最后,slow 即为处理好的数组的长度。
特别地,数组的前两个数必然可以被保留,因此对于长度不超过 2 的数组,我们无需进行任何处理,对于长度超过 2 的数组,我们直接将双指针的初始值设为 2 即可。
时间复杂度: O ( n ) O(n) O(n)
class Solution {
public int removeDuplicates(int[] nums) {
if (nums.length<=2) {
return nums.length;
}
int slow = 2;
for (int fast=2;fast<nums.length;fast++) {
if (nums[fast]!=nums[slow-2]) {
nums[slow] = nums[fast];
slow++;
}
}
return slow;
}
}
2.有序数组去重保留k位重复数的通法
由于是保留 k 个相同数字,对于前 k 个数字,我们可以直接保留
对于后面的任意数字,能够保留的前提是:与当前写入的位置前面的第 k 个元素进行比较,不相同则保留
class Solution {
public int removeDuplicates(int[] nums) {
return process(nums, 2); //传入不同k值
}
int process(int[] nums, int k) {
int idx = 0;
for (int x : nums) {
if (idx < k || nums[idx - k] != x)
nums[idx++] = x;
}
return idx;
}
}
283.移动零
283.移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
1.必须在原数组上操作,不能拷贝额外的数组。
2.尽量减少操作次数。
双指针法
相当于对整个数组用双指针法移除元素0,然后slow之后都是移除元素0的冗余元素,最后把这些元素都赋值为0就可以了。
class Solution {
public void moveZeroes(int[] nums) {
int slow = 0;
for (int fast=0;fast<nums.length;fast++) {
if (nums[fast]!=0) {
nums[slow++] = nums[fast];
}
}
for (int i=slow;i<nums.length;i++) {
nums[i]=0; //从slow以后都赋值为0
}
}
}
四、左右指针
977.有序数组的平方
977.有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1: 输入:nums = [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 [16,1,0,9,100],排序后,数组变为 [0,1,9,16,100]
示例 2: 输入:nums = [-7,-3,2,3,11] 输出:[4,9,9,49,121]
1.暴力排序解法
将数组中每个数平方,再排序
时间复杂度:
O
(
n
log
n
)
O(n\log n)
O(nlogn)
2.双指针法(左右指针法)
数组是有序的, 负数平方后可能成为最大数。
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
可以考虑双指针法,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k–] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k–] = A[i] * A[i]; 。

(图片来自代码随想录)
时间复杂度: O ( n ) O(n) O(n)
class Solution {
public int[] sortedSquares(int[] nums) {
int left = 0;
int right = nums.length - 1;
int[] result = new int[nums.length];
int idx = result.length - 1;
while (left<=right) {
if (nums[left]*nums[left]>nums[right]*nums[right]) {
result[idx--] = nums[left]*nums[left];
left++;
} else {
result[idx--] = nums[right]*nums[right];
right--;
}
}
return result;
}
}
344. 反转字符串 (数组)
344. 反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O ( 1 ) O(1) O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:[“h”,“e”,“l”,“l”,“o”]
输出:[“o”,“l”,“l”,“e”,“h”]
示例 2:
输入:[“H”,“a”,“n”,“n”,“a”,“h”]
输出:[“h”,“a”,“n”,“n”,“a”,“H”]
双指针
分别指向字符串首尾,交换。
class Solution {
public void reverseString(char[] s) {
for (int i=0,j=s.length-1;i<s.length/2;i++,j--) {
char temp = s[i];
s[i] = s[j];
s[j] = temp;
}
}
}
交换时可以用位运算写法:异或运算
class Solution {
public void reverseString(char[] s) {
int l = 0;
int r = s.length - 1;
while (l < r) {
s[l] ^= s[r]; //构造 a ^ b 的结果,并放在 a 中
s[r] ^= s[l]; //将 a ^ b 这一结果再 ^ b ,存入b中,此时 b = a, a = a ^ b
s[l] ^= s[r]; //a ^ b 的结果再 ^ a ,存入 a 中,此时 b = a, a = b 完成交换
l++;
r--;
}
}
}
18. 四数之和
18. 四数之和
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例: 给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。 满足要求的四元组集合为: [ [-1, 0, 0, 1], [-2, -1, 1, 2], [-2, 0, 0, 2] ]
双指针法
和15.三数之和是一个思路,都是使用双指针法。一样的道理,五数之和、六数之和等等都采用这种解法。
四数之和的双指针解法是两层for循环nums[j] + nums[i]为确定值,依然是循环内有left和right下标作为双指针,找出nums[j] + nums[i] + nums[left] + nums[right] == target的情况。四数之和的双指针解法就是将原本暴力
O
(
n
4
)
O(n^4)
O(n4)的解法,降为
O
(
n
3
)
O(n^3)
O(n3)的解法
时间复杂度: O ( n 3 ) O(n^3) O(n3)
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for (int i=0;i<nums.length;i++) {
if (i>0&&nums[i]==nums[i-1]) continue;//去重
for (int j=i+1;j<nums.length;j++) {
if(j>i+1&&nums[j]==nums[j-1]) continue;//去重
int left =j+1;
int right = nums.length-1;
while (right>left) {
//nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出
if (nums[i]+nums[j]>target-(nums[left]+nums[right])) {
right--;
} else if (nums[i]+nums[j]<target-(nums[left]+nums[right])) {
left++;
} else {
res.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));
while (right>left&&nums[right]==nums[right-1]) right--;
while (right>left&&nums[left]==nums[left+1]) left++;
left++;
right--;
}
}
}
}
return res;
}
}
167. 两数之和 II - 输入有序数组
167. 两数之和 II - 输入有序数组
870. 优势洗牌
870. 优势洗牌
回文子串问题
动规做法见 动态规划——子序列问题
647. 回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:“abc” 输出:3 解释:三个回文子串: “a”, “b”, “c”
示例 2:
输入:“aaa” 输出:6 解释:6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”
提示:
输入的字符串长度不会超过 1000 。
首先确定回文串的中心位置,就是找中心然后向两边扩散看是不是对称的就可以了,遇到不是回文的时候结束。
在遍历中心点的时候,要注意中心点有两种情况:一个元素可以作为中心点,两个元素也可以作为中心点。
这两种情况可以放在一起计算,也可分别计算,思路更清晰。
class Solution {
public int countSubstrings(String s) {
int res = 0;
for (int i = 0; i < s.length(); i++) {
res += extend(s,i,i,s.length()); // 以i为中心
res += extend(s,i,i+1,s.length()); // 以i和i+1为中心
}
return res;
}
int extend(String s, int left, int right, int len) {
int res = 0;
while (left>=0 && right<len && s.charAt(left)==s.charAt(right)) {
left--;
right++;
res++;
}
return res;
}
}
class Solution {
public int countSubstrings(String s) {
int len, ans = 0;
if (s == null || (len = s.length()) < 1) return 0;
//总共有2 * len - 1个中心点
for (int i = 0; i < 2 * len - 1; i++) {
//通过遍历每个回文中心,向两边扩散,并判断是否回文字串
//有两种情况,left == right,right = left + 1,这两种回文中心是不一样的
int left = i / 2, right = left + i % 2;
while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
//如果当前是一个回文串,则记录数量
ans++;
left--;
right++;
}
}
return ans;
}
}
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
双指针中心扩散法
class Solution {
public String longestPalindrome(String s) {
String res = "";
for (int i = 0; i < s.length(); i++) {
// 以 s[i] 为中心的最长回文子串
String s1 = palindrome(s, i, i);
// 以 s[i] 和 s[i+1] 为中心的最长回文子串
String s2 = palindrome(s, i, i + 1);
res = res.length() > s1.length() ? res : s1;
res = res.length() > s2.length() ? res : s2;
}
return res;
}
// 在 s 中寻找以 s[l] 和 s[r] 为中心的最长回文串
String palindrome(String s, int l, int r) {
while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) {
// 双指针,向两边展开
l--; r++;
}
// 返回以 s[l] 和 s[r] 为中心的最长回文串
return s.substring(l + 1, r);
}
}