学习目标：

学习二重积分，我会采取以下几个步骤：

1. 了解基本概念：首先我会学习二重积分的定义及其意义，了解二重积分的性质和特点，以及二重积分的计算方法。

2. 理解二重积分的几何意义：我会通过画图的方式，探究二重积分的几何意义。我会尝试将二重积分理解为对一个平面区域进行加权求和，从而帮助我理解二重积分的物理和几何意义。

3. 掌握二重积分的计算方法：我会学习如何将二重积分转化为累次积分，掌握直角坐标系下和极坐标系下的二重积分的计算方法，并了解变量替换和换序积分等计算技巧。

4. 学习应用：在掌握了二重积分的基本概念和计算方法之后，我会学习如何应用二重积分来解决实际问题，例如计算平面图形的重心、质心、面积等等。

5. 做练习：最后，我会做一些相关的习题和练习，以巩固所学知识，并提高解决问题的能力。

需要注意的是，对于不同的人来说，学习的难点和重点也可能不同，因此我会根据自己的实际情况，调整学习方法和策略，以更有效地掌握二重积分的知识。

 

从曲顶柱体的体积公式中，我们可以得到以下启发：

1. 利用二重积分可以求取曲顶柱体的体积，也可以求取其他形状的立体体积。
2. 通过确定积分区域的边界，选择合适的坐标系和积分顺序，可以简化积分计算。
3. 积分计算需要精确严谨，需要仔细审题、画图、确定积分区域和积分顺序等步骤，尤其是要注意被积函数的奇偶性、周期性等特征，避免漏项和误差。
4. 积分的应用不仅仅局限于计算几何问题，还可以应用于各种实际问题的建模和求解。

 

 

 

 

 

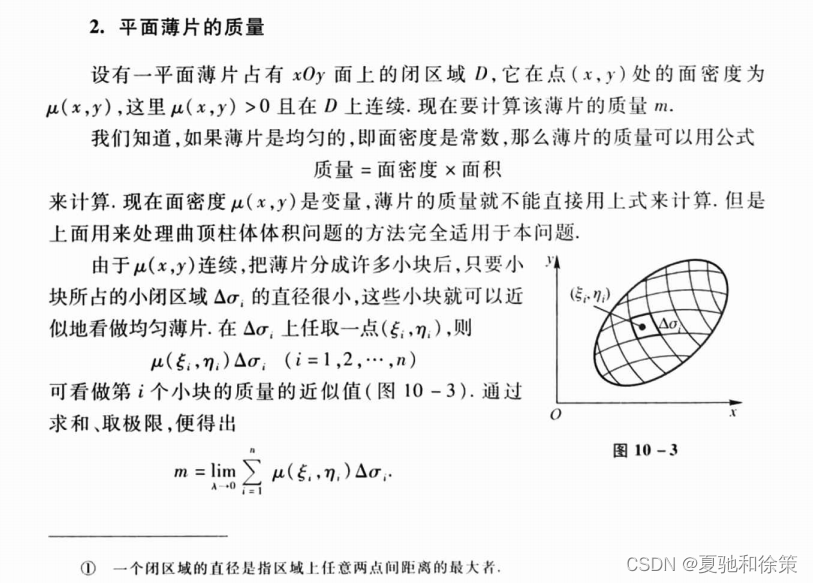
从用二重积分求平面薄片的质量的例子中，我们可以得到以下启发：

1. 二重积分可以用于计算平面区域的面积、质量等物理量。
2. 在使用二重积分计算物理量时，需要将物理量密度（例如质量密度）与微小面积相乘，形成微小质量元。
3. 二重积分求解平面薄片的质量时，需要确定积分区域及其边界方程，并根据实际情况选择合适的积分顺序。
4. 对于非简单连通区域，需要将其分解为若干简单连通区域，再通过适当的积分顺序求解总面积或总质量。