离散卡尔曼滤波基本理论

卡尔曼预报器、平滑器可以参考之前的博客：(2条消息) 卡尔曼滤波器_KPer_Yang的博客-CSDN博客

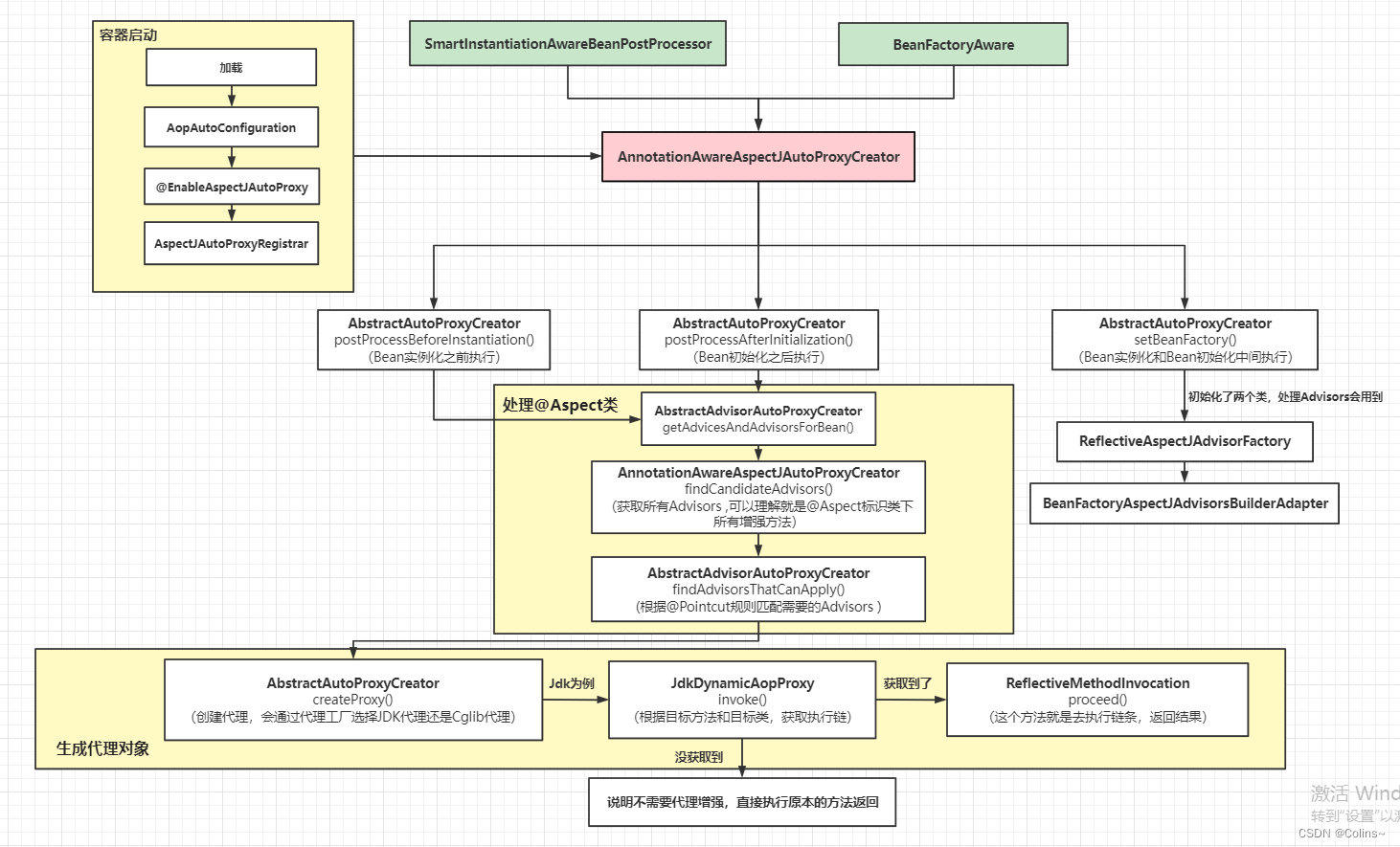
下面贴上一张图¹，很直观：分成时间更新和测量更新两步，其中的$K$和$P$有可能随着时间推移变成常数，但是多数情况是变化的，如果是常数，可以离线计算在线使用，可以减少很多在线计算量。$K$代表着观测值和状态空间计算值的不同比重，得到一个估计值作为输出。初始化观测噪声协方差矩阵$R$可以使用离线数据。初始化过程噪声矩阵$Q$比较困难。可以使用另一个卡尔曼滤波器离线进行估计，再实际使用。

陀螺仪的卡尔曼滤波参数初始化可以参考这种（其中q和r参数尤为重要，一般得通过实验测试得到）：²

1. init_x：待测量的初始值，如有中值一般设成中值
2. init_p：后验状态估计值误差的方差的初始值
3. q：预测（过程）噪声方差
4. r：测量（观测）噪声方差。以陀螺仪为例，测试方法是：保持陀螺仪不动，统计一段时间内的陀螺仪输出数据。数据会近似正态分布，按3σ原则，取正态分布的(3σ)^2作为r的初始化值。

numpy实现

import numpy as np


class DiscreteSystem:
    """
    离散系统
    """

    def __int__(self,
                A: np.array, B: np.array, Q: np.array,
                H: np.array, R: np.array, X: np.array,
                Z: np.array, U: np.array):
        self.A = A  # 状态转移矩阵 nxn
        self.B = B  # 输入矩阵 nxl,只有加入控制量才有用到，一般滤波没有用到
        self.Q = Q  # 过程噪声 p(w)~N(0, Q),Q难估算，离散数据需要另一个卡尔曼滤波进行估算
        self.H = H  # 观测矩阵 mxn
        self.R = R  # 测量噪声 p(v)~N(0, R),R可以通过离线数据计算
        self.X = X  # 状态变量 nx1
        self.Z = Z  # 观测值 mx1
        self.U = U  # 控制量 lx1


class Kalman_Filter:
    """
    卡尔曼滤波
    """

    def __init__(self, discrete_system: DiscreteSystem, estimation_init: np.array, P_init: np.array):
        """
        初始化
        :param discrete_system: 离散系统
        :param estimation_init: 估计值初始化
        :param P_init: P初始化
        """
        self.discrete_system = discrete_system
        self.estimation = estimation_init
        self.P = P_init  # P会趋向于稳定

    def forward(self, Z: np.array) -> np.array:
        """
        一步卡尔曼滤波
        :param Z:观测值
        :return:估计值
        """
        self.estimation = Z
        self.discrete_system.Z = Z
        X_right_top_hat_ = self.discrete_system.A @ self.estimation + self.discrete_system.B @ self.discrete_system.U
        P_right_top_ = self.discrete_system.A @ self.P @ np.transpose(self.discrete_system.A) + self.discrete_system.Q
        # 计算增益
        K = P_right_top_ @ np.transpose(self.discrete_system.H) \
            @ np.linalg.inv(self.discrete_system.H @ P_right_top_ @ np.transpose(self.discrete_system.H) + self.discrete_system.R)
        self.estimation = X_right_top_hat_ + K @ (Z - self.discrete_system.H @ X_right_top_hat_)
        # 计算误差协方差矩阵，会随着不断迭代趋于稳定
        self.P = P_right_top_ - K @ self.discrete_system.H @ P_right_top_
        return self.estimation


if __name__ == '__main__':
    # 1、初始化离散系统DiscreteSystem
    # 2、初始化卡尔曼滤波 Kalman_Filter
    # 3、使用观测值循环调用 卡尔曼滤波step
    ...

参考：

---

1. An Introduction to the Kalman Filter ↩︎

2. Kalman滤波器从原理到实现 - 莫水千流 - 博客园 (cnblogs.com) ↩︎