学习是一个长久而艰苦的过程，但不学习则更艰苦。

文章目录

• 引言
• 正文
• • 函数的定义
  • 全函数
  • 覆盖运算
  • 函数的性质（重点）
  • • 单射
    • 满射
    • 双射
  • 递归函数
  • • 良定义

引言

笔者一直觉得在计算机这一学科的学习中，离散数学是极为重要的知识基础。离散化的思想体现在计算机学科的方方面面。举例来说，“像素”这一概念是我们日常生活中耳熟能详的，将一个图片拆分成一个个极微小的像素，就是利用了离散化的思想。为了帮助大家打好离散数学的思维基础，笔者新开一个专栏，对《离散数学导学》这本书做一个精炼，使其更易理解。这篇文章是这个专栏的第五部分，主要介绍第9章。
1-3章传送门
4-5章传送门
6-7章传送门
8章传送门

正文

函数的定义

我们在中学数学中学过函数的定义是一个自变量最多对应一个因变量，在离散数学中相似。
一个关系中，如果每一个源头中的元素最多只映射到一个目标中的元素，那么这个关系称为一个函数。

全函数

如果函数源头的所有元素都能映射到目标的某个元素，这个函数就称为全函数。下图是全函数的一个例子：

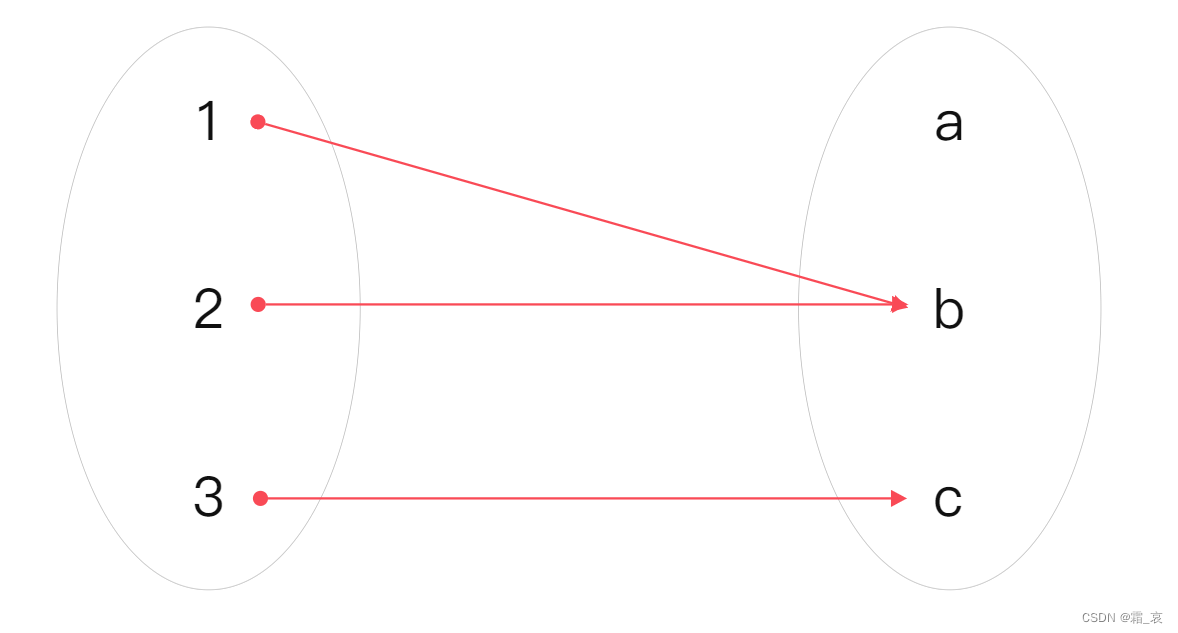
覆盖运算

覆盖运算A⊕B，我们用例子来说明：

1. 设下图是函数A和B的映射关系（第一行是源头，第二行是目标）：
   
2. 则A⊕B是：
   

则A⊕B得出的就是：逐个检查B中的序偶，如果发现序偶的源头也在A中，那么直接用B中的序偶的目标替换掉A中相对应序偶的目标，如果是新的序偶（源头不出现在A中），将这个序偶直接加入A。

函数的性质（重点）

单射

如果一个函数中源头的一个元素最多只映射到目标中的一个元素，那么这个函数是一个单射函数。注意：也可以映射到0个元素，即不映射。下图是一个单射函数：

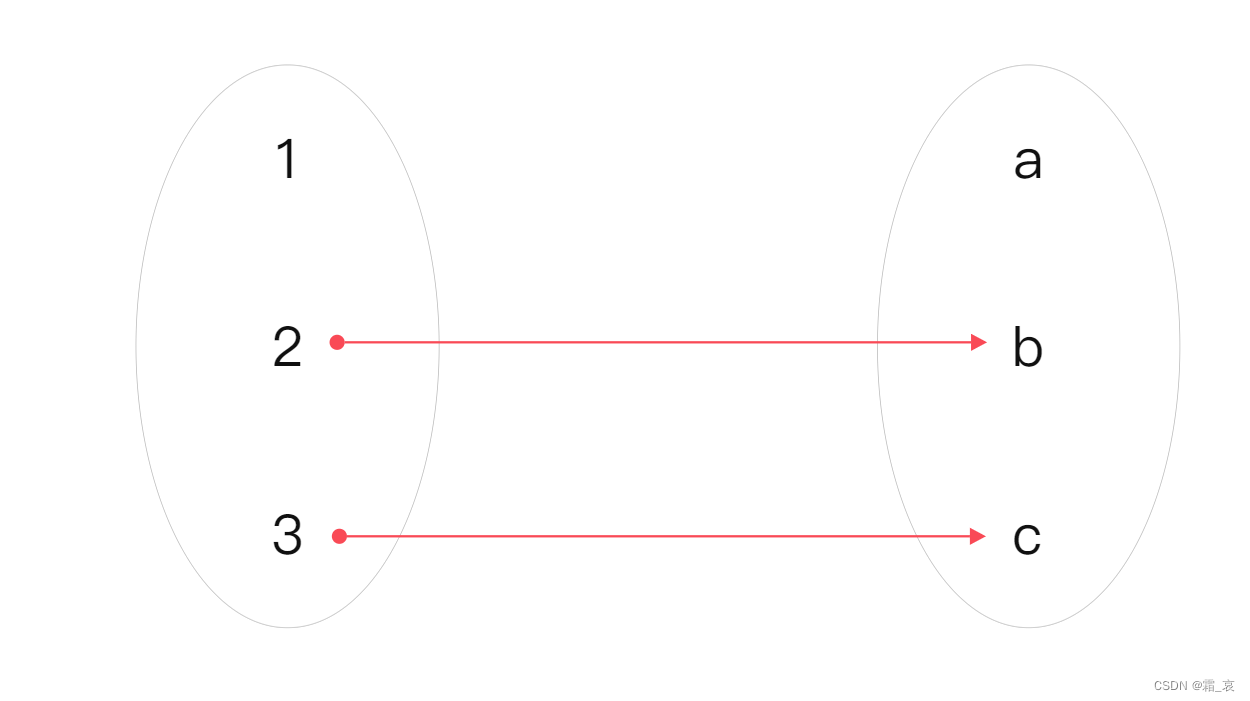
满射

如果目标中的所有元素都有映射其的源头元素，那么这个函数是满射的。下图是一个满射函数：

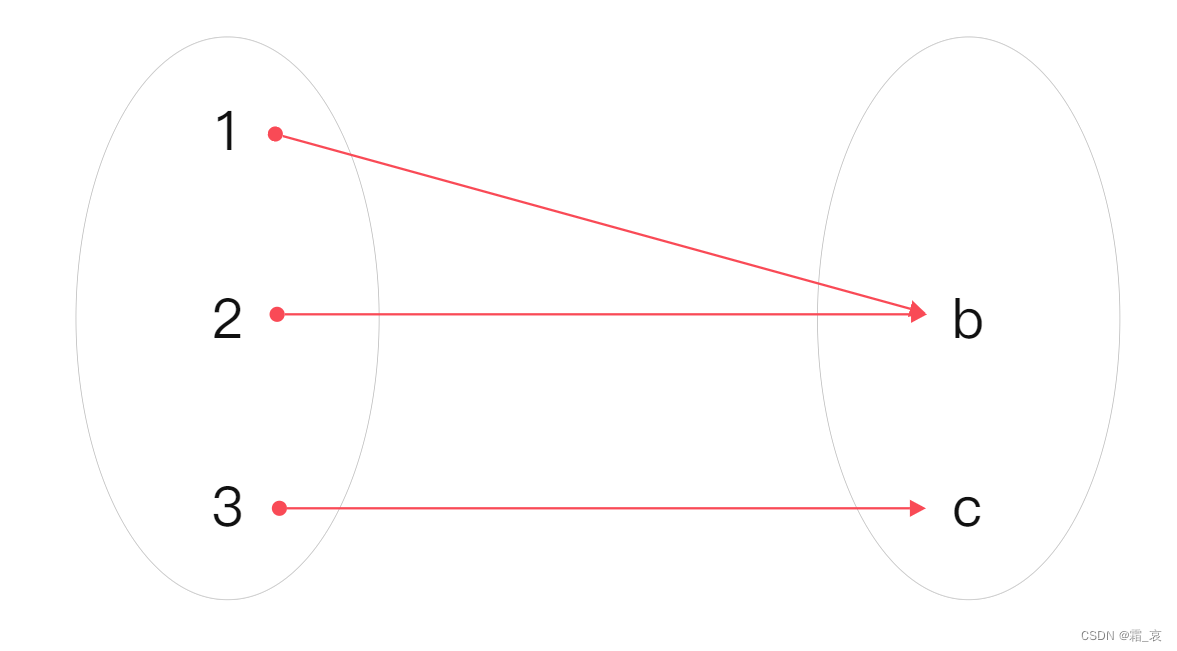
双射

既是单射又是满射的函数是双射函数。下图是一个双射函数：

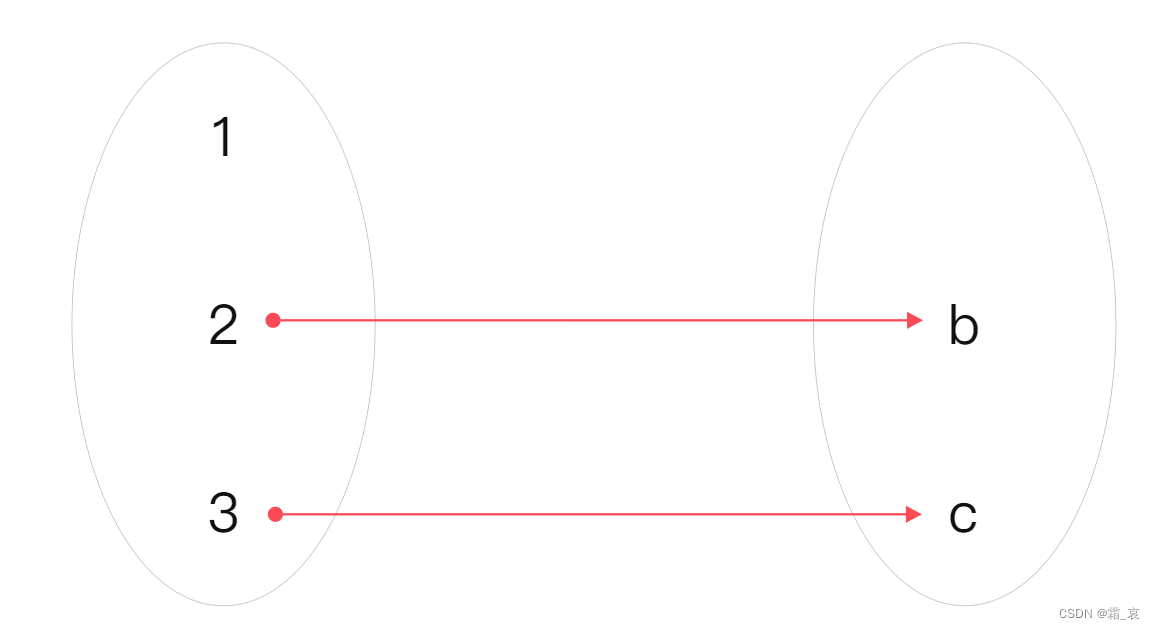
递归函数

任意由其自身定义的函数称作递归函数。作为一个经典的递归函数，我们用斐波那契函数来举个例子：

f(1)=f(2)=1
n>2时，f(n)=f(n-1)+f(n-2)

在这个函数中，除了f(1)和f(2)之外，其他函数值由自身的某些函数值定义。

良定义

我们称下面的递归函数是良定义的：

1. 存在基底值
2. 基底值之外的函数每次引用自身求值，函数自变量都更靠近基底值。

从定义不难看出，良定义的递归函数其实就是最后能求出所有函数值的递归函数。斐波那契函数就是一个良定义的递归函数。