文章目录
- 一:图像增强概述
- 二:基于灰度级变换的图像增强
- (1)线性灰度级变换
- A:基本线性灰度级变换
- B:分段线性灰度级变换
- ①:定义
- ②:截取式灰度变换
- ③:窗切片
- (2)非线性灰度级变换
- A:对数变换
- B:指数变换
- C:幂次变换
- D:程序
一:图像增强概述
图像增强(Image Enhancement):指不考虑图像降质原因,利用各种数学方法和变换手段,增强图像中人们感兴趣部分或提高有用的图像特征的清晰度。从图像质量来看,图像增强提高了图像的可懂度,改善了图像的视觉效果
例如在现实场景中,针对那些对比度较差、视觉效果不好的图像,我们就可以利用图像增强改善视觉质量

图像增强可分为如下几种
- 基于灰度级变换的图像增强
- 基于直方图修正的图像增强
- 基于照度反射模型的图像增强
- 基于模糊技术的图像增强
- 基于伪彩色处理的图像增强
- 其他图像增强方法
二:基于灰度级变换的图像增强
基于灰度级变换的图像增强:设原始图像为 f ( x , y ) f(x,y) f(x,y),增强后的图像为 g ( x , y ) g(x,y) g(x,y), T ( r ) T(r) T(r)表示灰度级变换函数,其中 r r r表示像素的灰度值。则增强后的图像可以表示为
g ( x , y ) = T ( f ( x , y ) ) g(x,y)=T(f(x,y)) g(x,y)=T(f(x,y))
其中, T ( r ) T(r) T(r)是一个非线性灰度级变换函数,它将原始图像的灰度级值映射到一个新的灰度级值。常见的灰度级变换函数包括线性变换、对数变换、幂次变换、伽马变换等。由于一般都是将过暗的图像灰度值进行重新映射,扩展灰度级范围,使其分布在整个灰度值区间,因此通常称为扩展
(1)线性灰度级变换
A:基本线性灰度级变换
基本线性灰度级变换 :设基本线性变换函数为 tan α \tan \alpha tanα,有
- α = 45 ° \alpha=45° α=45°:灰度范围不变
- α > 45 ° \alpha>45° α>45°:拉伸灰度范围
- α < 45 ° \alpha<45° α<45°:压缩灰度范围
g ( x , y ) = f ( x , y ) ⋅ tan α g(x,y)=f(x,y)\cdot \tan \alpha g(x,y)=f(x,y)⋅tanα
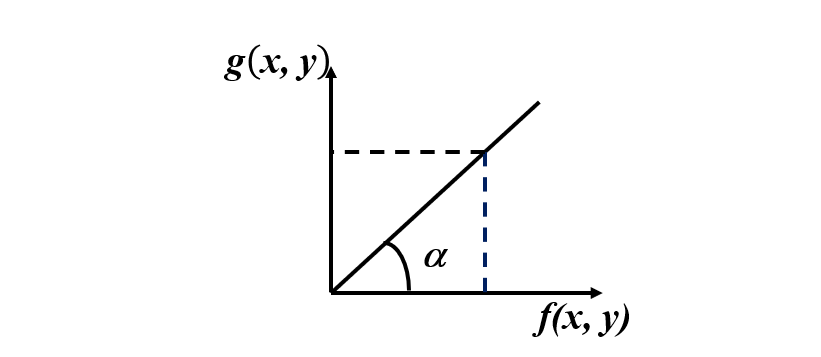
下图是一个变换示例
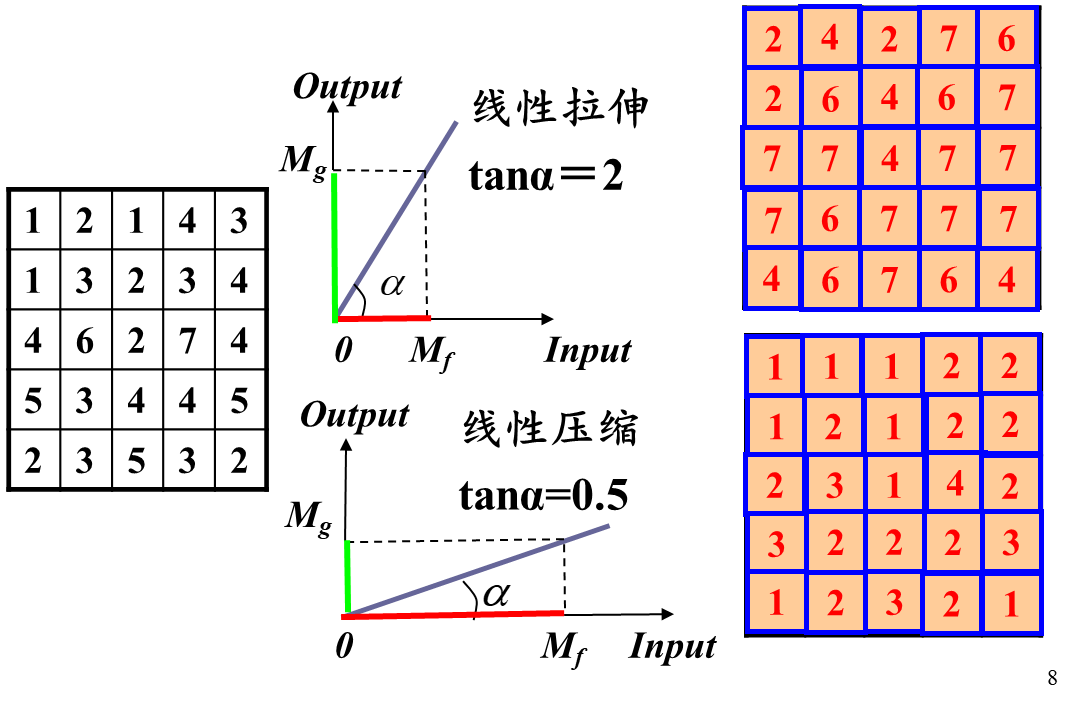
下图为实际效果

B:分段线性灰度级变换
①:定义
分段线性灰度级变换:设原始图像为 f ( x , y ) f(x,y) f(x,y),增强后的图像为 g ( x , y ) g(x,y) g(x,y),则有
g ( x , y ) = { c a f ( x , y ) 0 ≤ f ( x , y ) < a d − c b − a [ f ( x , y ) − a ] + c a ≤ f ( x , y ) < b L − 1 − d L − 1 − b [ f ( x , y ) − b ] + d b ≤ f ( x , y ) < L − 1 g(x, y)=\left\{\begin{array}{cc}\frac{c}{a} f(x, y) & 0 \leq f(x, y)<a \\\frac{d-c}{b-a}[f(x, y)-a]+c & a \leq f(x, y)<b \\\frac{L-1-d}{L-1-b}[f(x, y)-b]+d & b \leq f(x, y)<L-1\end{array}\right. g(x,y)=⎩ ⎨ ⎧acf(x,y)b−ad−c[f(x,y)−a]+cL−1−bL−1−d[f(x,y)−b]+d0≤f(x,y)<aa≤f(x,y)<bb≤f(x,y)<L−1
其中,参数a、b、c、d为确定三段线段斜率的常数
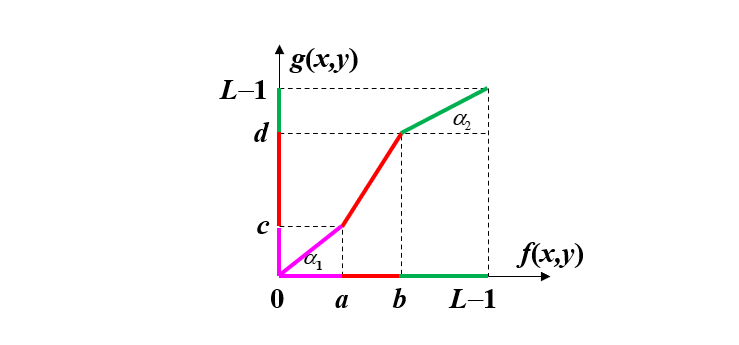
下图为具体实例

②:截取式灰度变换
若用户仅对感兴趣范围 [a, b) 线性拉伸,则:
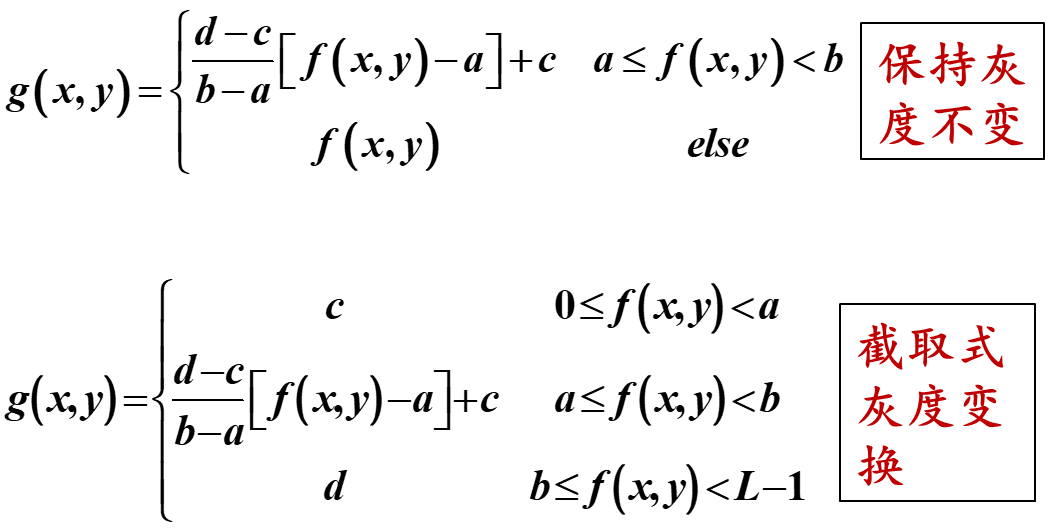
实现如下效果

MATLAB实现:相关函数如下,具体解释可看MATLAB帮助手册
J= imadjust(I,[LOW_IN;HIGH_IN ], [LOW_OUT; HIGH_OUT], GAMMA )NEWMAP= imadjust(MAP, [LOW_IN;HIGH_IN], [LOW_OUT;HIGH_OUT],GAMMA )RGB2 = imadjust (RGB1,...)
imadjust是MATLAB中用于图像灰度级调整的函数,用于将图像的灰度级范围调整到指定范围。其函数原型如下
J = imadjust(I,[low_in high_in],[low_out high_out],gamma)
其中,I是输入的灰度图像,[low_in high_in]是输入灰度级范围,[low_out high_out]是输出灰度级范围,gamma是伽马变换参数。
imadjust函数的具体功能包括:
- 将图像的灰度级范围调整到指定范围。
- 增强图像的对比度。
- 进行非线性的灰度级变换。
imadjust函数的参数[low_in high_in]和[low_out high_out]用于指定输入和输出的灰度级范围,可以控制输出图像的灰度级分布。参数gamma可以用于进行伽马变换,增强图像的暗部细节,同时保留图像的亮度信息
代码如下
Image=im2double(rgb2gray(imread('lotus.bmp')));%读取图像,灰度化并转换为double型
[h,w]=size(Image); %获取图像尺寸
NewImage1=zeros(h,w);NewImage2=zeros(h,w); %新图像初始化
NewImage3=Image;
a=30/256; b=100/256; c=75/256; d=200/256; %参数设置
for x=1:w
for y=1:h
if Image(y,x)<a
NewImage1(y,x)=Image(y,x)*c/a;
elseif Image(y,x)<b
NewImage1(y,x)=(Image(y,x)-a)*(d-c)/(b-a)+c;%分段线性变换
else
NewImage1(y,x)=(Image(y,x)-b)*(1-d)/(1-b)+d;
end
if Image(y,x)>a && Image(y,x)<b
NewImage3(y,x)=(Image(y,x)-a)*(d-c)/(b-a)+c; %高低端灰度保持
end
end
end
NewImage2=imadjust(Image,[a;b],[c;d]); %截取式灰度变换
imwrite(Image,'gray_lotus.bmp');
imwrite(NewImage1,'lotus1.bmp');
imwrite(NewImage2,'lotus2.bmp');
imwrite(NewImage3,'lotus3.bmp');
imshow(Image);title('原始lotus图像');
figure;imshow(NewImage1);title('分段线性灰度级变换图像');
figure;imshow(NewImage2);title('截取式灰度级变换图像');
figure;imshow(NewImage3);title('高低端灰度级保持不变图像');
Python实现:使用Python实现上述同样的功能
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# Read the image and convert it to grayscale
image = cv2.imread('lotus.bmp')
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
image = image.astype('float64')/255.0
# Get the image size
h, w = image.shape
# Initialize new images
new_image1 = np.zeros((h, w))
new_image2 = np.zeros((h, w))
new_image3 = image.copy()
# Set the parameters
a = 30/256
b = 100/256
c = 75/256
d = 200/256
# Apply the gray level transformations
for x in range(w):
for y in range(h):
if image[y,x] < a:
new_image1[y,x] = image[y,x]*c/a
elif image[y,x] < b:
new_image1[y,x] = (image[y,x]-a)*(d-c)/(b-a)+c
else:
new_image1[y,x] = (image[y,x]-b)*(1-d)/(1-b)+d
if image[y,x] > a and image[y,x] < b:
new_image3[y,x] = (image[y,x]-a)*(d-c)/(b-a)+c
new_image2 = cv2.convertScaleAbs(image, alpha=(d-c)/(b-a), beta=c-a*(d-c)/(b-a))
# Save the images
cv2.imwrite('gray_lotus.bmp', image*255.0)
cv2.imwrite('lotus1.bmp', new_image1*255.0)
cv2.imwrite('lotus2.bmp', new_image2)
cv2.imwrite('lotus3.bmp', new_image3*255.0)
# Display the images
plt.figure(figsize=(12, 10))
plt.subplot(2, 2, 1)
plt.imshow(image, cmap='gray')
plt.title('原始lotus图像')
plt.axis('off')
plt.subplot(2, 2, 2)
plt.imshow(new_image1, cmap='gray')
plt.title('分段线性灰度级变换图像')
plt.axis('off')
plt.subplot(2, 2, 3)
plt.imshow(new_image2, cmap='gray')
plt.title('截取式灰度级变换图像')
plt.axis('off')
plt.subplot(2, 2, 4)
plt.imshow(new_image3, cmap='gray')
plt.title('高低端灰度级保持不变图像')
plt.axis('off')
plt.show()
③:窗切片
窗切片(window slicing):是一种用于图像增强的特殊分段线性变换技术。在窗口切片中,输入图像的灰度级被分成多个区间,每个区间被映射到一个特定的输出灰度级范围内,使用户能够增强图像中特定灰度级范围内的细节
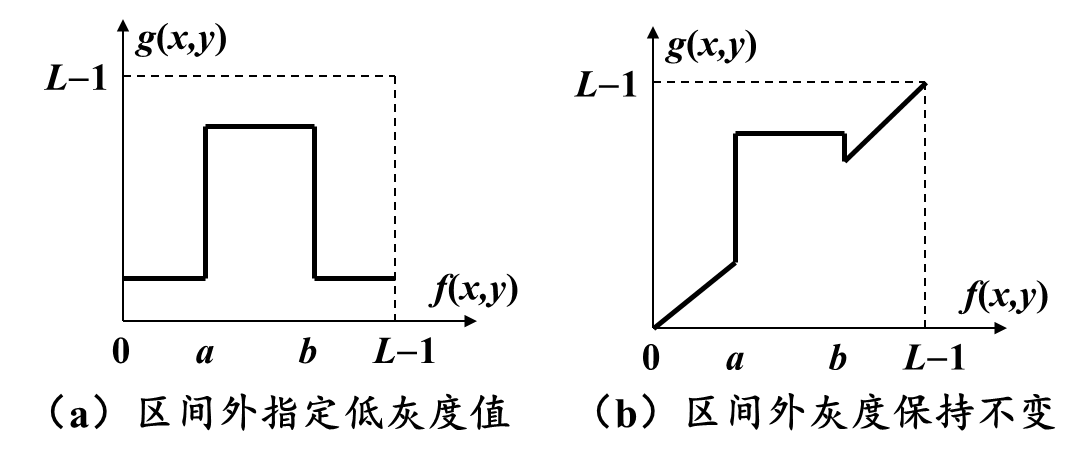
例如,假设我们有一张灰度级范围从0到255的输入图像,我们想增强中等灰度级范围内(即100-150)的细节。我们可以将灰度级分成三个区间:0-99、100-150和151-255。然后,我们可以分别对每个区间应用线性变换,将中间区间内的灰度级映射到更高的输出灰度级范围,同时保持其他区间内的灰度级不变。如果输入灰度级位于特定范围(即窗口)内,则输出灰度级将使用以下公式映射到新的范围内
- x x x是输入灰度级
- a a a和 b b b是窗口的下限和上限
- c c c和 d d d是输出范围的下限和上限
f
(
x
)
=
(
x
−
a
)
∗
(
(
d
−
c
)
/
(
b
−
a
)
)
+
c
f(x) = (x - a) * ((d-c)/(b-a)) + c
f(x)=(x−a)∗((d−c)/(b−a))+c
实现如下效果
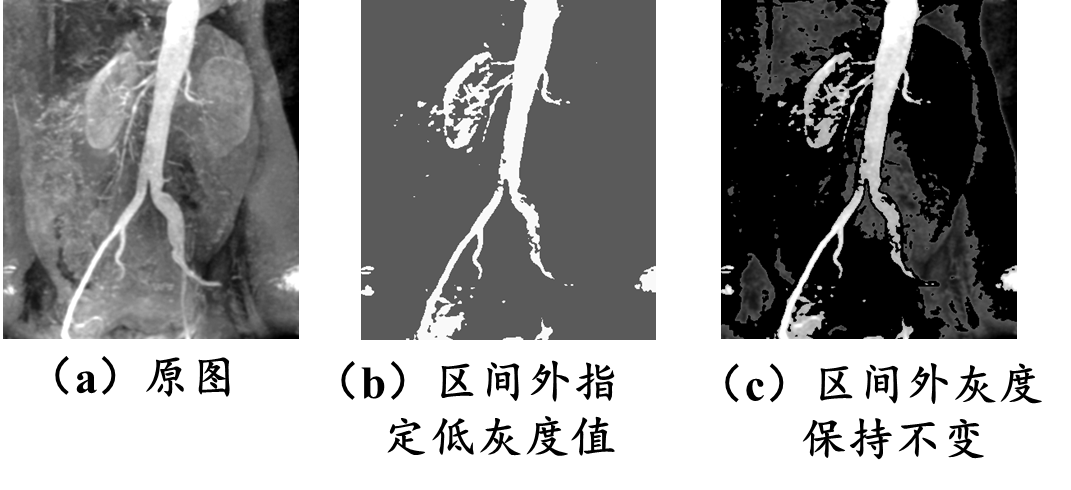
MATLAB实现:
Image=im2double(imread('AG.jpg'));%读取图像并转换为double型
[h,w]=size(Image); %获取图像尺寸
NewImage1=zeros(h,w);
NewImage2=Image;
a=170/256; b=200/256; c=90/256; d=250/256; %参数设置
for x=1:w
for y=1:h
if Image(y,x)<a
NewImage1(y,x)=c;
else
NewImage1(y,x)=d; %图5-6(a)窗切片方法
end
if Image(y,x)>c && Image(y,x)<a
NewImage2(y,x)=0; %图5-6(b)窗切片方法
end
end
end
imwrite(NewImage1,'AG1.bmp');
imwrite(NewImage2,'AG2.bmp');
imshow(Image);title('ACG图像');
figure;imshow(NewImage1);title('图5-6(a)窗切片图像');
figure;imshow(NewImage2);title('图5-6(b)窗切片图像');
Python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
Image = cv2.imread('AG.jpg', cv2.IMREAD_GRAYSCALE).astype(np.float64) / 255.0
h, w = Image.shape[:2]
NewImage1 = np.zeros((h, w), dtype=np.float64)
NewImage2 = Image.copy()
a, b, c, d = 170/256, 200/256, 90/256, 250/256
for x in range(w):
for y in range(h):
if Image[y, x] < a:
NewImage1[y, x] = c
else:
NewImage1[y, x] = d
if Image[y, x] > c and Image[y, x] < a:
NewImage2[y, x] = 0
cv2.imwrite('AG1.bmp', NewImage1*255.0)
cv2.imwrite('AG2.bmp', NewImage2*255.0)
plt.subplot(1, 3, 1), plt.imshow(Image, cmap='gray'), plt.title('ACG图像')
plt.subplot(1, 3, 2), plt.imshow(NewImage1, cmap='gray'), plt.title('图5-6(a)窗切片图像')
plt.subplot(1, 3, 3), plt.imshow(NewImage2, cmap='gray'), plt.title('图5-6(b)窗切片图像')
plt.show()
(2)非线性灰度级变换
A:对数变换
对数变换:设原始图像为 f ( x , y ) f(x,y) f(x,y),增强后的图像为 g ( x , y ) g(x,y) g(x,y),则有
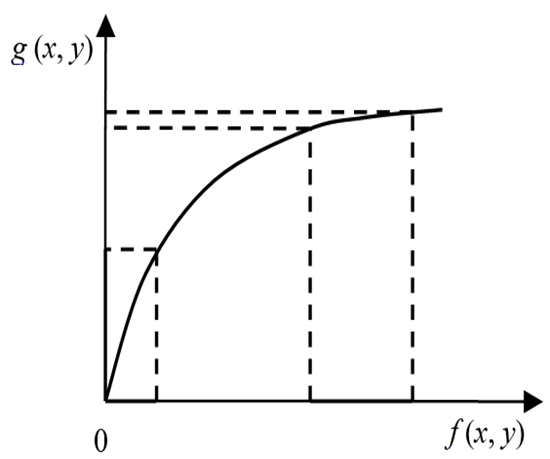
g ( x , y ) = c ⋅ log ( f ( x , y ) + 1 ) g(x,y)=c \cdot \log(f(x,y)+1) g(x,y)=c⋅log(f(x,y)+1)
对数变换压缩图像高灰度区,扩展图像低灰度区,一般适用于处理过暗图像
B:指数变换
指数变换:设原始图像为 f ( x , y ) f(x,y) f(x,y),增强后的图像为 g ( x , y ) g(x,y) g(x,y),则有
g ( x , y ) = b c ⋅ [ f ( x , y ) − a ] = − 1 g(x,y)=b^{c \cdot [f(x,y)-a]}=-1 g(x,y)=bc⋅[f(x,y)−a]=−1
指数变换扩展图像高灰度区,压缩图像低灰度区,一般适用于处理过亮图像
C:幂次变换
指数变换:设原始图像为 f ( x , y ) f(x,y) f(x,y),增强后的图像为 g ( x , y ) g(x,y) g(x,y),则有
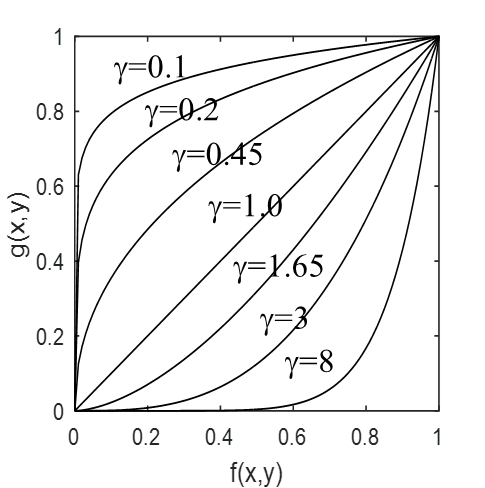
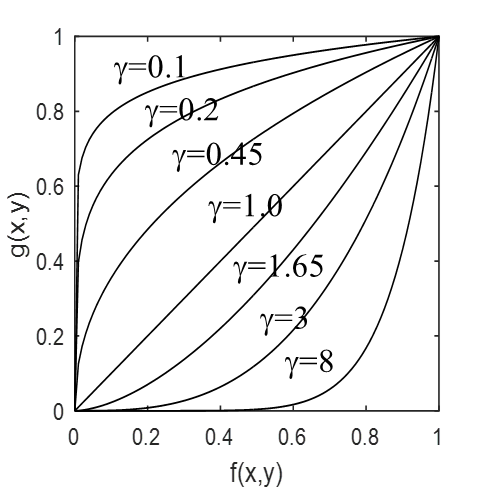
g ( x , y ) = c ⋅ [ f ( x , y ) ] γ g(x,y)=c \cdot [f(x,y)]^{\gamma} g(x,y)=c⋅[f(x,y)]γ
幂次变换常用于图像获取、打印和显示的各种装置设备的伽马校正,因此幂次变换也称为伽马变换
D:程序
实现如下效果

MATLAB实现:
Image=(rgb2gray(imread('Goldilocks.bmp')));
imwrite(Image,'GGoldilocks.bmp');
Image=double(Image);
NewImage1=46*log(Image+1); %对数函数非线性灰度级变换
NewImage2=185*exp(0.325*(Image-225)/30)+1;%指数函数非线性灰度级变换
a=0.5; c=1.1;
NewImage3=[(Image/255).^a]*255*c;
imwrite(uint8(NewImage1),'Goldilocks1.bmp');
imwrite(uint8(NewImage2),'Goldilocks2.bmp');
imwrite(uint8(NewImage2),'Goldilocks3.bmp');
imshow(Image,[]);title('Goldilocks灰度图像');
figure;imshow(NewImage1,[]);title('对数函数非线性灰度级变换');
figure;imshow(NewImage2,[]);title('指数函数非线性灰度级变换');
figure;imshow(NewImage3,[]);title('幂次函数非线性灰度级变换');
Python实现:
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 读取图像并转为灰度图
img = cv2.imread('Goldilocks.bmp')
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 保存灰度图
cv2.imwrite('GGoldilocks.bmp', img_gray)
# 将图像转为浮点型
img_gray = np.float32(img_gray)
# 对数函数非线性灰度级变换
new_img1 = 46 * np.log(img_gray + 1)
# 指数函数非线性灰度级变换
new_img2 = 185 * np.exp(0.325 * (img_gray - 225) / 30) + 1
# 幂次函数非线性灰度级变换
a = 0.5
c = 1.1
new_img3 = ((img_gray / 255) ** a) * 255 * c
# 保存变换后的图像
cv2.imwrite('Goldilocks1.bmp', new_img1)
cv2.imwrite('Goldilocks2.bmp', new_img2)
cv2.imwrite('Goldilocks3.bmp', new_img3)
# 显示原始灰度图像及变换后的图像
plt.figure()
plt.imshow(img_gray, cmap='gray')
plt.title('Goldilocks灰度图像')
plt.show()
plt.figure()
plt.imshow(new_img1, cmap='gray')
plt.title('对数函数非线性灰度级变换')
plt.show()
plt.figure()
plt.imshow(new_img2, cmap='gray')
plt.title('指数函数非线性灰度级变换')
plt.show()
plt.figure()
plt.imshow(new_img3, cmap='gray')
plt.title('幂次函数非线性灰度级变换')
plt.show()