堆排序

堆排序，听名字就是要对堆进行排序，但当我们是无序数据时，首先我们就需要建立一个堆
在这里插入图片描述

建堆

这里让我们来回忆一下前面的堆，改变堆的数据顺序我们有向上调整和向下调整。

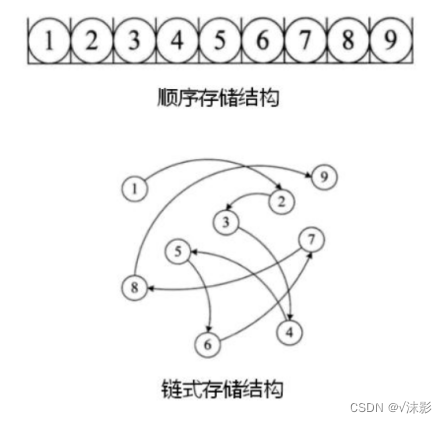
向上调整建堆

在这里插入图片描述
这是向上调整堆的思路。

当我们对一个数据进行向下调整时，首先要保证上面都成堆。
在这里插入图片描述

那我们从最上面一个一个进行向上调整
不就可以保证上面都是堆了嘛。

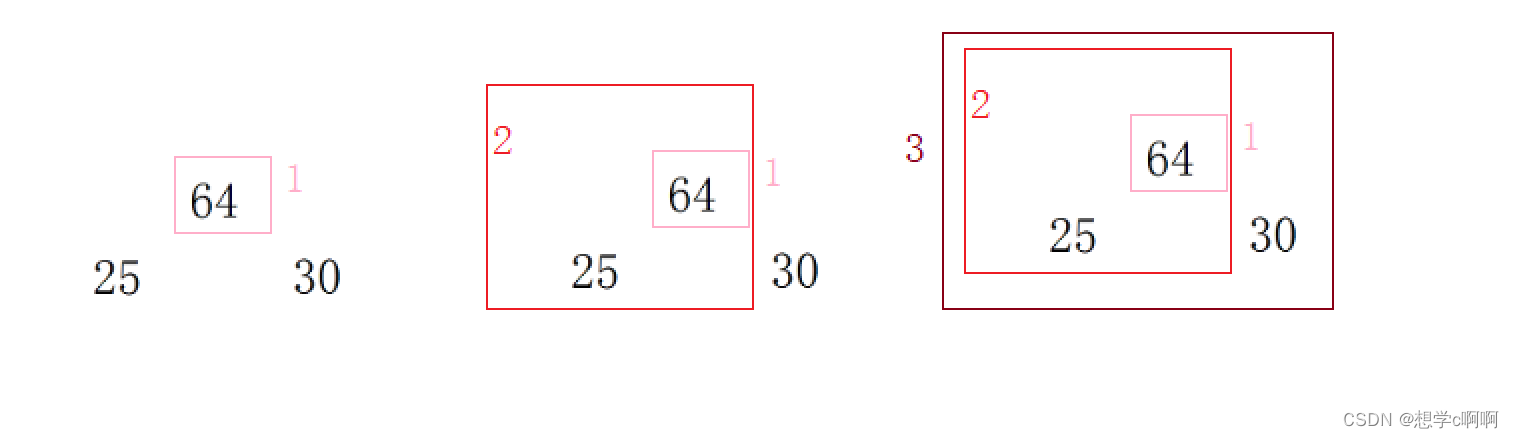
在这里插入图片描述
1：arr[0]进行建堆
2：对arr[0],arr[1]进行建堆
3：对arr[0],arr[2],arr[3]进行建堆
………………………………
这样就能保证对堆的第n个数据进行调整时，n以上的所有数据都成堆

void Swap(int* arr, int x, int y)
{
	int tmp = arr[x];
	arr[x] = arr[y];
	arr[y] = tmp;
}
void adjustup(int* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(a, child, parent);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
			break;
	}
}
void creatheap(int* arr,int size)
{
	for (int i = 0; i < size; i++)
	{
		adjustup(arr, i);
	}
}
int main()
{
	int arr[20] = { 54,76,23,58,167,367,235,651,764,126,538,12,79,23,46,13,67,38,30,15 };
	creatheap(arr,20);
	for (int i = 0; i < 20; i++)
		printf("%d ", arr[i]);
	return 0;
}

在这里插入图片描述
这样我们就得到了一个大根堆。
（大根堆和小根堆就差在adjustup所以这里就不举大根堆的例子了）

向下建堆

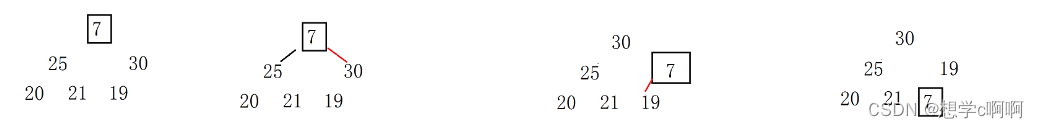
在这里插入图片描述
这是向下调整的思路，同向上调整一样，向下调整则是要求下面的数都是堆。

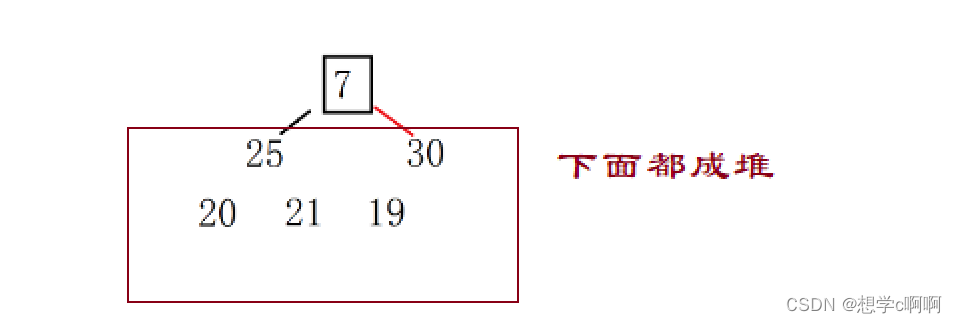
在这里插入图片描述

所以比较于前面的向上调整是从上面一个一个调整，向下调整是要从下面开始一个一个调整

那我们就要从最底下的19一个一个开始调整嘛？
其实也不用这么麻烦
我们可以从30开始的最后一个根开始一个一个调整。
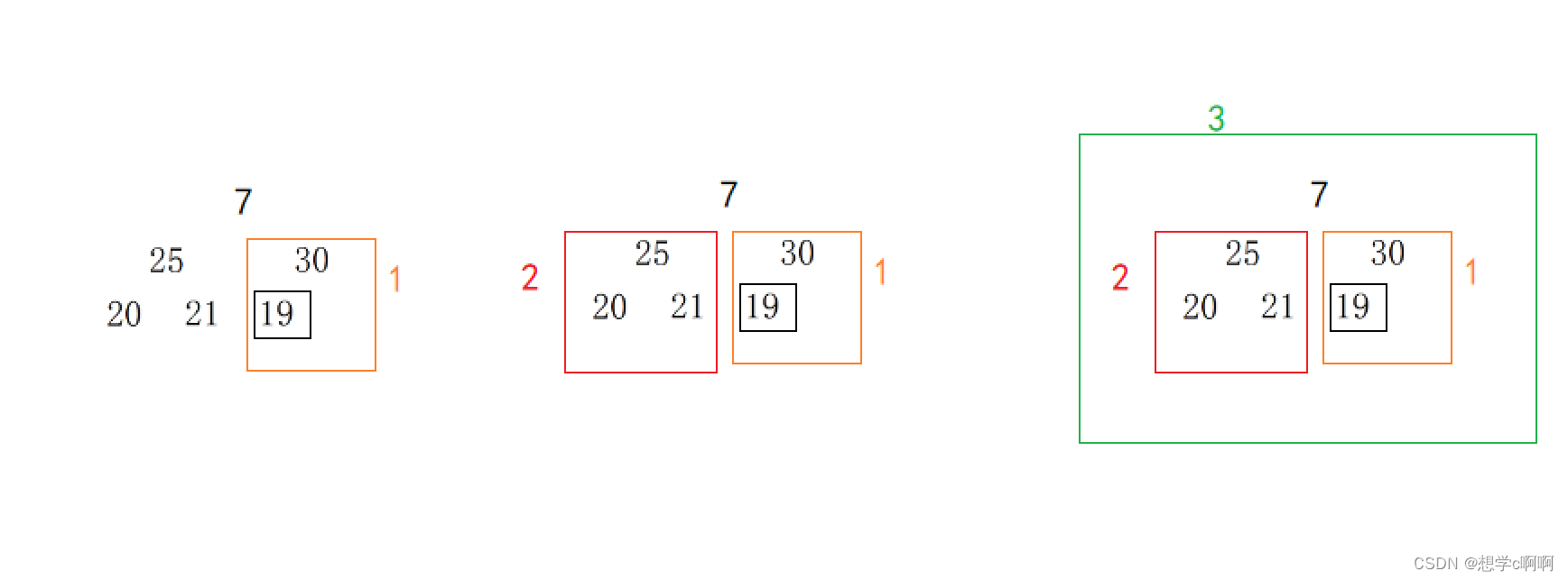
在这里插入图片描述
1：调整30这个最后一个根
2：调整25这个根
3：调整7这个根，前面调整了30和25，保证了n下面的数据都成一个堆

void Swap(int* arr, int x, int y)
{
	int tmp = arr[x];
	arr[x] = arr[y];
	arr[y] = tmp;
}
void AdjustDown(int* a, int n, int parent)
{
	int child = 2 * parent + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child] < a[child+1])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(a, child, parent);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void creatheap(int* arr,int size)
{
	for (int i = (size-1-1)/2; i>=0; i--)
	{
		AdjustDown(arr,size,i);
	}
}
int main()
{
	int arr[20] = { 54,76,23,58,167,367,235,651,764,126,538,12,79,23,46,13,67,38,30,15 };
	creatheap(arr,20);
	for (int i = 0; i < 20; i++)
		printf("%d ", arr[i]);
	return 0;
}

这样就建好了一个大根堆。

堆排序

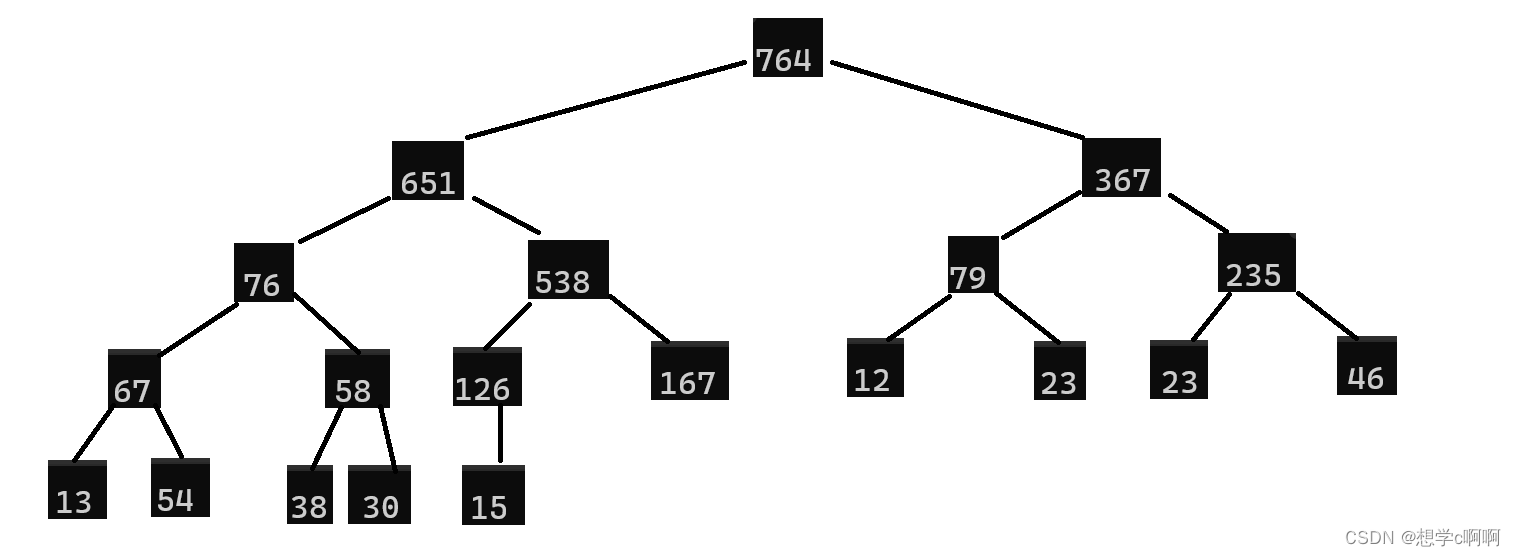
在这里插入图片描述
当我们建立好一个大根堆时

我们发现大根堆的特点是其最顶端的数据一定是最大的一个数。
这里我们就能想到
为什么我们不每次取出顶端最大的值，然后再进行向下调整，然后再得到最大值，不断循环呢？

这里确实是这样一个思路，但是我们在我们取出最大值时，那最大值要用什么数来填补呢？
这个时候我们就能想到堆的删除数据操作了。
在这里插入图片描述
这就是我们的交换删除法。
完美契合堆排序的要求。

void creatheap(int* arr,int size)
{
//前面建堆的部分
	for (int i = (size-1-1)/2; i>=0; i--)
	{
		AdjustDown(arr,size,i);
	}
	int end = size - 1;
	//排序部分
	while (end >= 0)
	{
		Swap(arr, 0, end);
		end--;
		AdjustDown(arr, end+1, 0);
	}
}