说明

闵老师的文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

day32 图的连通性检测

1.思路

1.1矩阵表示

看一个矩阵M,Vi->Vj值不为0,则说明vi能到vj(对角线表示自身)
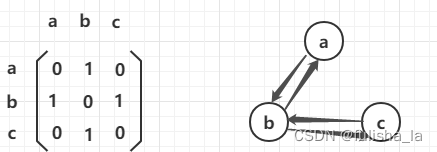
在这里插入图片描述

1.2.矩阵相乘

矩阵相乘运算（如MM = M^2 ）。矩阵运算：求一个结点的运算 $\displaystyle\sum_{i=1}^{n} m_{ik}\cdot m_{kj}$ 。

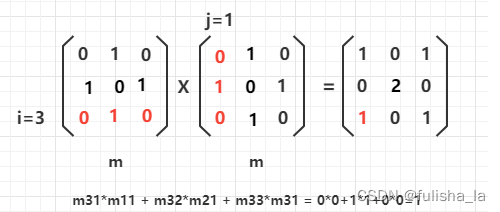
结合上面的图，三个结点1 2 3; m32 = 1代表3到2有路径，m32m21 = 1 代表代表3到2有路径，且2到1有路径，进而3到1有路径，只不过需要通过2这个结点。如这里m31m11+m32m21+m33*m31=1表明3到1 只有一条路径。

1.3结合矩阵运算思考图的连通性。

(1) 连通
当Vi->Vj不能直连时(若最后能相连)则其中会经过一个或几个中间结点。Vi->Vk,Vk->Vj.
所以假设 $m_{ik}\cdot m_{kj}=1$ 可以理解为从Vi->Vk有路径，Vk->Vj有路径，则相乘为1,则Vi->Vj就存在一条路径，且长度是为2的路径连通。通过公式
$\sum_{k=1}^{n}m_{ik}\cdot m_{kj}$ 若值等于0说明不连通，若值大于0说明连通，且可以知道Vi到Vj有几条路。
(2) 不连通
假设 $m_{ik}\cdot m_{kj}=0$ 表示不存在Vi->Vj这样的路径.
所以矩阵相乘可以去看矩阵的连通性。进一步 $M^{n}$ 就是长度为m路的数目。

2.代码

再来看文章中： $M_{a} = M^{0} + M^{1} + ...+ M^{n-1}$ 有n个结点，为什么只需要到n-1？因为假设有n个结点，最多需要n-1条边连起来。今天这个根据矩阵的运算来判断图的连通性，以前我只知道通过遍历图看图的连通性，今天从数学角度去思考图的连通性，有收获！再去读代码写代码就很好理解了（我觉得主要的逻辑代码就在getConnectivity方法中的step3中的这一个for循环中）。

package graph;

import matrix.IntMatrix;
public class Graph {

    IntMatrix connectivityMatrix;

    /**
     * The first constructor.
     * @param paraNumNodes The number of nodes in the graph.
     */
    public Graph(int paraNumNodes){
        connectivityMatrix = new IntMatrix(paraNumNodes, paraNumNodes);
    }

    /**
     * The second constructor.
     * @param paraMatrix The data matrix.
     */
    public Graph(int[][] paraMatrix){
        connectivityMatrix = new IntMatrix(paraMatrix);
    }

    @Override
    public String toString(){
        return "This is the connectivity matrix of the graph.\r\n" + connectivityMatrix;
    }

    /**
     * Get the connectivity of the graph.
     * @return
     */
    public boolean getConnectivity() throws Exception {
        // Step 1. Initialize accumulated matrix.
        IntMatrix tempConnectivityMatrix = IntMatrix.getIdentityMatrix(connectivityMatrix.getData().length);

        //Step 2. Initialize
        IntMatrix tempMultipliedMatrix = new IntMatrix(connectivityMatrix);

        //Step 3. Determine the actual connectivity.
        for (int i = 0; i < connectivityMatrix.getData().length - 1; i++){
            // M_a = M_a + M^k
            tempConnectivityMatrix.add(tempMultipliedMatrix);
            // M^k
            tempMultipliedMatrix = IntMatrix.multiply(tempMultipliedMatrix, connectivityMatrix);
        }

        // Step 4. Check the connectivity.
        System.out.println("The connectivity matrix is: " + tempConnectivityMatrix);
        int[][] tempData = tempConnectivityMatrix.getData();
        for (int i = 0; i < tempData.length; i++) {
            for (int j = 0; j < tempData.length; j++){
                if (tempData[i][j] == 0){
                    System.out.println("Node " + i + " cannot reach " + j);
                    return false;
                }
            }
        }
        return true;
    }

    /**
     * Unit test for getConnectivity.
     */
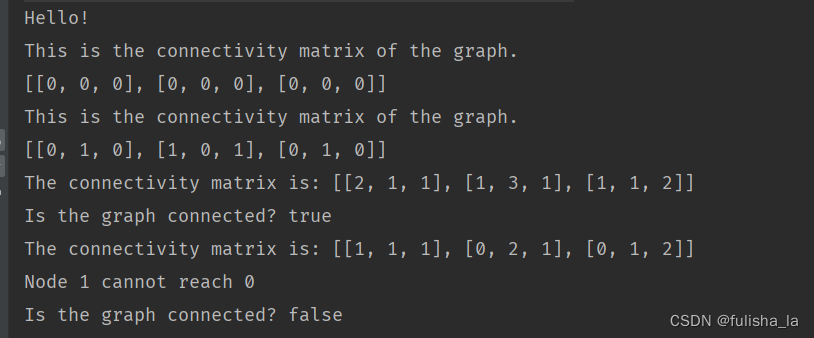
    public static void getConnectivityTest(){
        int[][] tempMatrix = { { 0, 1, 0 }, { 1, 0, 1 }, { 0, 1, 0 } };
        Graph tempGraph2 = new Graph(tempMatrix);
        System.out.println(tempGraph2);

        boolean tempConnected = false;
        try {
            tempConnected = tempGraph2.getConnectivity();
        } catch (Exception ee) {
            System.out.println(ee.getMessage());
        }
        System.out.println("Is the graph connected? " + tempConnected);

        //Test a directed graph. Remove one arc to form a directed graph.
        tempGraph2.connectivityMatrix.setValue(1, 0, 0);
        tempConnected = false;
        try {
            tempConnected = tempGraph2.getConnectivity();
        } catch (Exception ee) {
            System.out.println(ee);
        }

        System.out.println("Is the graph connected? " + tempConnected);

    }

    public static void main(String[] args) {
        System.out.println("Hello!");
        Graph tempGraph = new Graph(3);
        System.out.println(tempGraph);

        // Unit test.
        getConnectivityTest();
    }
}

在这里插入图片描述