@[TOC](P4158 [SCOI2009]粉刷匠(分组背包问题))

一、问题

[SCOI2009]粉刷匠

题目描述

windy有 N 条木板需要被粉刷。 每条木板被分为 M 个格子。 每个格子要被刷成红色或蓝色。

windy每次粉刷，只能选择一条木板上一段连续的格子，然后涂上一种颜色。 每个格子最多只能被粉刷一次。

如果windy只能粉刷 T 次，他最多能正确粉刷多少格子？

一个格子如果未被粉刷或者被粉刷错颜色，就算错误粉刷。

输入格式

第一行包含三个整数，N M T。

接下来有N行，每行一个长度为M的字符串，'0’表示红色，'1’表示蓝色。

输出格式

包含一个整数，最多能正确粉刷的格子数。

样例 #1

样例输入 #1

3 6 3
111111
000000
001100

样例输出 #1

16

提示

30%的数据，满足 1 <= N,M <= 10 ； 0 <= T <= 100 。

100%的数据，满足 1 <= N,M <= 50 ； 0 <= T <= 2500 。

二、分析

我们将粉刷的次数看作背包的容量，正确粉刷的个数看作价值。将每一条木板看作一个物品组。那么这道题就转化成了，我们将$t$分到不同的物品组里，我们能够得到的最大价值。

那么现在这道题的难点就转化成了，对于一个木板，在不同粉刷次数的情况下，我们能够粉刷的最大的正确方格数？

我们就先来解决这个问题。

$g[i][j][k]$表示，对第$i$条木板的前$j$个格子至多进行$k$次涂色，在该条件下，我们能够获得的最大价值。

如果我们第$k$次不涂色的话，
$$g[i][j][k]=g[i][j][k-1]$$

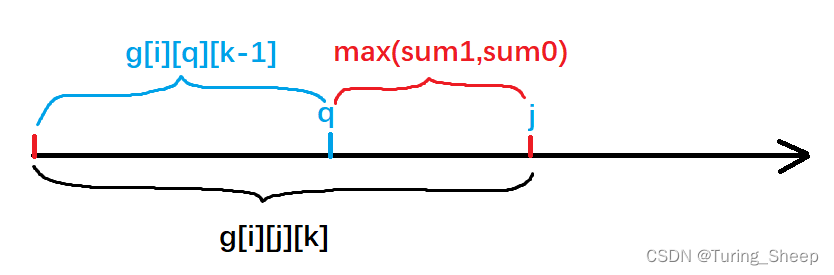
如果第$k$次涂色的话，我们可以去枚举第$k$次涂色的区间。该区间所涂的颜色取决于该区间内是蓝色多还是红色多，也就是说我们需要提前统计出所有区间内的红色块和蓝色块的个数。该操作可以通过前缀和算法高效地实现。

转移的过程，我们可以通过枚举第$k$次涂色的区间的左端点。不妨将该区间内的1的个数记作$sum1$，0的个数记作$sum0$。则转移方程如下：
$$g[i][j][k]=max(g[i][j][k],g[i][q][k-1]+max(sum1,sum0))$$

当我们求出$g$数组之后，后续过程只需要套一个分组背包的板子即可。
我们让$f[i][j]$表示在前$i$个板子中涂$j$次颜色，所能获得的最大正确格子数。
状态转移即：
$$f[i][j]=max(f[i-1][j-k]+g[i][m][k],f[i][j])$$
其中$k$是分给第$i$个板子的粉刷次数，$m$是该木板的格子数目。

三、代码

#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int f[51][2550],sum_1[51][60], sum_0[51][60];
int g[51][51][2550];
int n,m,t;
char s[60][60];

void solve()
{
	cin >> n >> m >> t;

	for(int i = 1; i <= n; i ++)
	{
		scanf("%s", s[i] + 1);
		for(int j = 1; j <= m; j ++ )
			if(s[i][j] == '1')
			{
				sum_1[i][j] = sum_1[i][j - 1] + 1;
				sum_0[i][j] = sum_0[i][j - 1];
			}
			else
			{
				sum_0[i][j] = sum_0[i][j - 1] + 1;
				sum_1[i][j] = sum_1[i][j - 1];
			}
	}

	for(int i = 1; i <= n; i ++)
	{
		for(int j = 1; j <= m; j ++)
			for(int k = 1; k <= m; k ++)
			{
				g[i][j][k] = g[i][j][k - 1];
				for(int q = 0; q < j; q ++)
				{
					int sum1 = sum_1[i][j] - sum_1[i][q];
					int sum0 = sum_0[i][j] - sum_0[i][q];
					g[i][j][k] = max(g[i][q][k - 1] + max(sum1, sum0), g[i][j][k]);
				}
			}
	}


	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= t; j ++ )
			for(int k=0;k<=min(j,m);k++)
			{
				f[i][j] = max(f[i][j], f[i - 1][j - k] + g[i][m][k]);
			}

	cout << f[n][t] << endl;
}

signed main()
{
	solve();
}