算法学习day57
- 1.力扣647. 回文子串
- 1.1 题目描述
- 1.2分析
- 1.3 代码
- 2.力扣 516.最长回文子序列
- 2.1 题目描述
- 2.2 分析
- 2.3 代码
- 3.参考资料
1.力扣647. 回文子串
1.1 题目描述
题目描述:
给定一个字符串,计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会视为不同的子串。
例1:
输入:“abc” 输出:3
解释:三个回文子串:“a” , “b”, “c”
例2:
输入:“aaa” 输出:6
解释:6个回文子串:“a” , “a” , “a” , “aa” , “aa”, “aaa”
注:回文子串是指在一个字符串中,从左往右读和从右往左读是一样的子串。
1.2分析
1.确定dp数组以及下标的含义
基于回文子串从左往右读和从右往左读是一样的子串。在判断字符串s是否是回文子串的时候,如果我们知道s[1]、s[2]、s[3]这个子串是回文的,那么只需要比较两端即s[0]、s[4]这两个元素是否相同,如果相同就是回文子串。
由上可知找到了一种递归关系,判断一个子字符串范围[i,j]是否回文,依赖于范围[i+1 , j -1].
所以定义dp数组为二维dp数组,区间范围[i , j] (左闭,右闭)的子串是否是回文子串,如果是为true否则false。
2.确定递推公式
分为两种情况:
(1)s[i] 与s[j]不相等
不相等,显然dp[i] [j] = false;
(2)s[i]与s[j]相等
(2.1) 下标i与下标j相同,是同一个字符例如a,当然是回文子串。
(2.2) 下标i与j相差为1,例如aa,也是回文子串。
(2.3) 下标i与j相差大于1,例如cabac,此时s[i]与s[j]已经相同了,都是c。看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是[i+1,j-1]区间,这个区间是不是回文子串就看dp[i + 1] [j - 1]是否为true。
递推公式如下:
if(s[i] == s[j]){
// 下标i 与 j相同,同一个字符例如a,当然是回文子串
// 下标i 与 j相差为1,例如aa,也是回文子串
if(j - i <=1){
result ++;
dp[i][j] = true;
}else if(dp[i+1][j-1]){
//下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
result ++;
dp[i][j] = true;
}
}
由于s[i] 与s[j]不等的时候,在初始化的时候初始化为false,所以在递推公式中没有体现。
3.dp数组如何初始化
dp[i] [j] 可以初始化为true吗?
答:不可以,还没有判断怎么都是回文子串了?所以dp[i] [j] 初始化为false
4.确定遍历顺序
由递推公式推导中**(2.3)可知dp[i+1] [j-1]是否为true,来推导dp[i] [j]是否为true的。**
dp[i + 1] [j - 1] 在 dp[i] [j]的左下角,i行数加1往下走,j列数减1往左走。所以是左下角。
显然从上到下,即:从i+1已知到i未知。从左到右,即:从j-1已知到j未知。
代码如下:
外层for循环从字符串的最后一个字符开始向前遍历,逐一枚举字符串中所有的起始位置i。
内层for循环从当前的起始位置i开始,向后枚举所有可能的终止位置j。由于回文子串必须左右对称,所以终止位置只能在起始位置i的右侧所以为(j < s.size())
for(int i = s.size() - 1 ; i >= 0 ; i--){
for(int j = i; j < s.size(); j++){
// 下标i 与 j相同,同一个字符例如a,当然是回文子串
// 下标i 与 j相差为1,例如aa,也是回文子串
if(s[i] == s[j]){
if(j - i <= 1){
result++;
dp[i][j] = true;
//下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
}else if(dp[i+1][j-1]){
result++;
dp[i][j] = true;
}
}
}
}
5.举例推导dp数组
输入:“aaa”,dp[i] [j]状态如下:
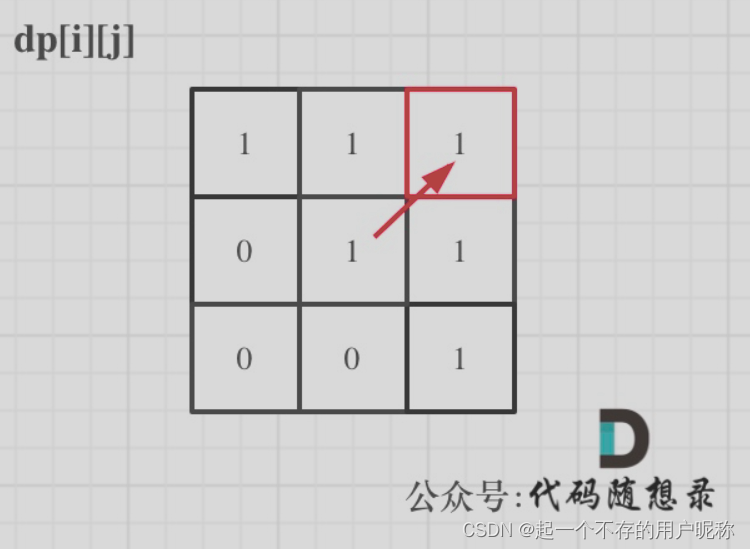
图中有6个true,所以就是有6个回文子串。
注:因为dp[i] [j]的定义,所以j一定是大于等于i的(j是右端i是左端),那么在填充dp[i] [j]的时候一定是只填充右上半部分。
1.3 代码
class Solution {
public:
int countSubstrings(string s) { // 计算 s 中回文子串的个数
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false)); // 动态规划数组,dp[i][j] 表示 s[i...j] 是否是回文子串
int result = 0; // 记录回文子串个数
for (int i = s.size() - 1; i >= 0; i--) { // 从字符串末尾开始遍历
for (int j = i; j < s.size(); j++) { // 遍历所有以 i 为左端点、以 j 为右端点的子串
// (2.1)下标i 与 j相同,同一个字符例如a,当然是回文子串
// (2.2)下标i 与 j相差为1,例如aa,也是回文子串
if (s[i] == s[j]) {
if (j - i <= 1) {
result++; // 回文子串个数加一
dp[i][j] = true; // 标记 dp[i][j] 为 true,表示 s[i...j] 是回文子串
// (2.3)下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
} else if (dp[i + 1][j - 1]) {
result++; // 回文子串个数加一
dp[i][j] = true; // 标记 dp[i][j] 为 true,表示 s[i...j] 是回文子串
}
}
}
}
return result; // 返回回文子串个数
}
};
2.力扣 516.最长回文子序列
2.1 题目描述
题目描述:
给定一个字符串s,找到其中最长的回文子序列,并返回该序列的长度,假设s的最大长度为1000.
例 1: 输入: “bbbab” 输出: 4 一个可能的最长回文子序列为 “bbbb”。
例 2: 输入:“cbbd” 输出: 2 一个可能的最长回文子序列为 “bb”。
注:回文子串是要连续的,回文子序列可不是连续的
2.2 分析
1.确定dp数组以及下标的含义
dp[i] [j]:字符串s在[i , j]范围内最长的回文子序列的长度为dp[i] [j].
2.确定递推公式
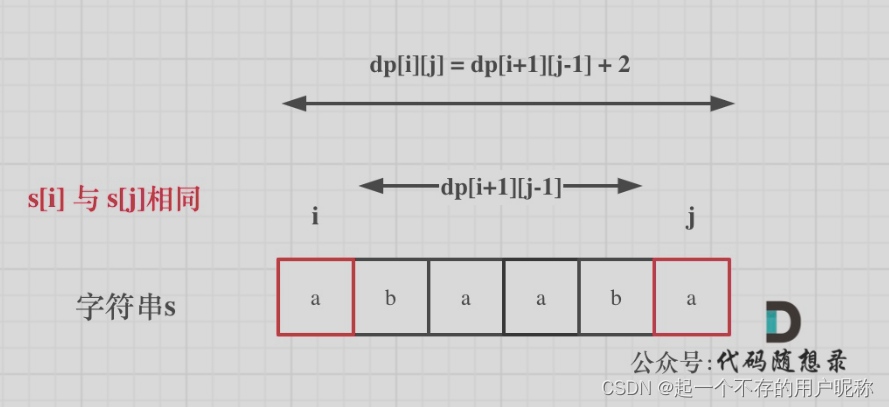
(1)如果s[i]与s[j]相同,那么dp[i] [j] = dp[i+1] [j-1] +2
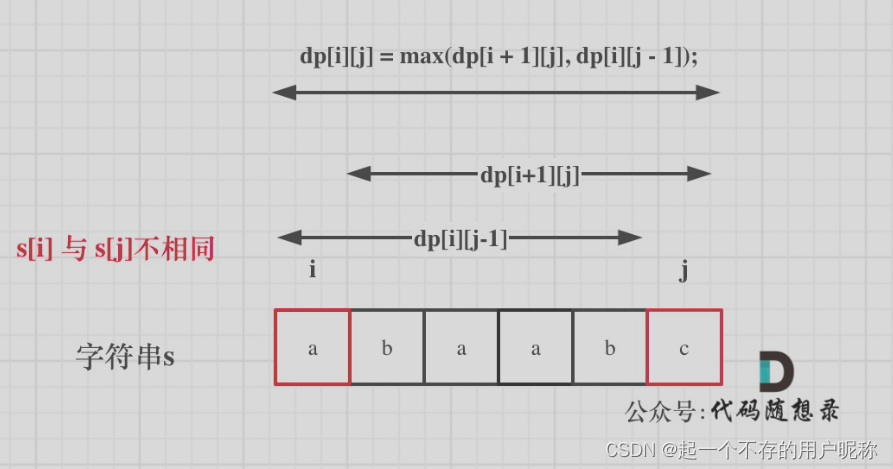
(2)如果s[i]与s[j]不相同,那么说明s[i]和s[j]的同时加入不能增加[i,j]区间回文子序列的长度,尝试分别加入s[i]、s[j]。看哪一个可以组成最长的回文子序列。
原为dp[i+1] [j-1]
(2.1)加入s[j]的回文子序列长度为dp[i+1] [j]
(2.2)加入s[i]的回文子序列长度为dp[i] [j-1]
其中dp[i] [j]取最大,即:dp[i] [j] = max(dp[i+1] [j], dp[i] [j-1])
代码如下:
if(s[i] == s[j]){
//(1)如果s[i]与s[j]相同,那么dp[i] [j] = dp[i+1] [j-1] +2
dp[i][j] = dp[i+1][j-1]+2;
}else{
// (2.1)加入s[j]的回文子序列长度为dp[i+1] [j]
// (2.2)加入s[i]的回文子序列长度为dp[i] [j-1
//其中dp[i] [j]取最大,即:dp[i] [j] = max(dp[i+1] [j], dp[i] [j-1])
dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
}
(1)、(2)的图如下:
3.dp数组如何初始
由递推公式:dp[i] [j] = dp[i+1] [j-1] + 2可知递推公式计算不到i和j相同的情况,手动初始一下。由前面if(s[i] == s[j]),可知i与j相同,那么dp[i] [j]一定是等于1的,是一个回文子序列。
将其他dp[i] [j] 初始为0,因为不能上来都初始1都认为是回文子序列。
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for(int i =0; i< s.size(); i++) dp[i][j] = 1;
4.确定遍历顺序
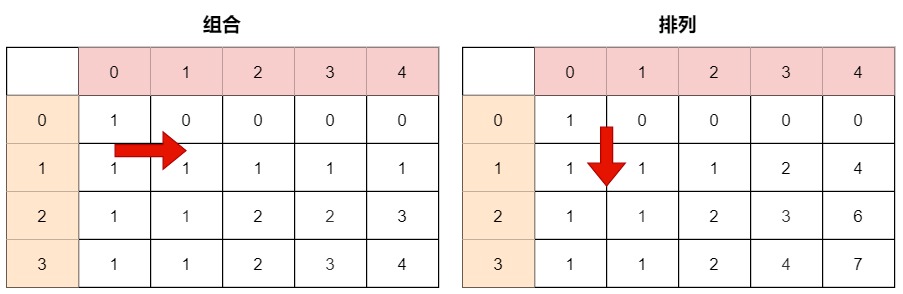
由递推公式可知dp[i] [j]依赖于dp[i+1] [j-1]、dp[i+1] [j] 、dp[i] [j-1],**遍历i的时候要从下到上,即从i+1到i。j从左到右,即从j-1到j。**递推顺序如图:
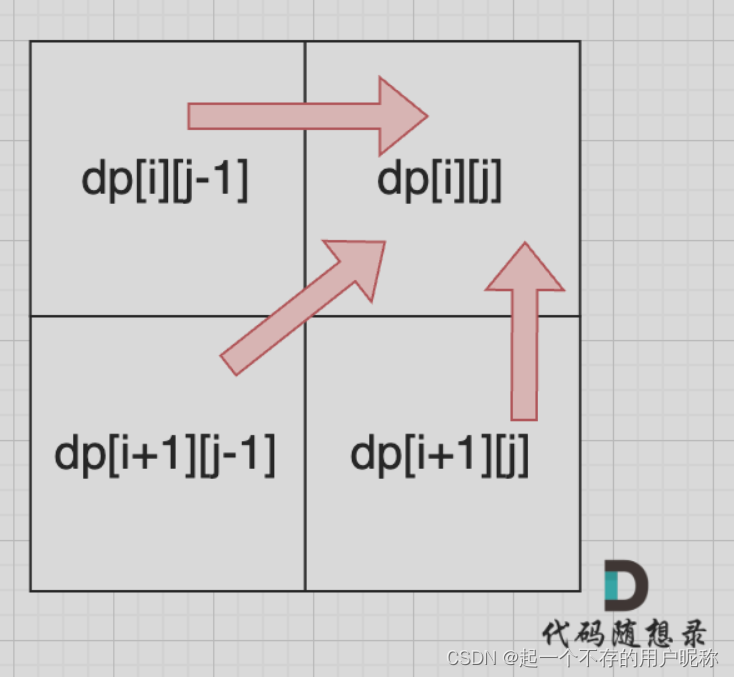
代码如下:
首先,外层循环从字符串末尾开始,从后往前遍历所有可能的起点,即子序列的左边界。内层循环则从起点的下一个位置开始,遍历到字符串末尾,即子序列的右边界。这样可以保证遍历到所有可能的子序列,而不会漏掉任何一个。
注意,内层循环的起点是i+1,而不是i,这是因为当子序列长度为1时,它也是回文子序列,需要特殊处理。如果内层循环从i开始,则会漏掉长度为1的回文子序列。因此,内层循环的起点需要从i+1开始。
for(int i = s.size() - 1 ; i >=0 ; i--){
for(int j = i+1 ; j< s.size(); j++){
//(1)如果s[i]与s[j]相同,那么dp[i] [j] = dp[i+1] [j-1] +2
if(s[i] == s[j]){
dp[i][j] = dp[i+1][j-1] +2;
}else{
// (2.1)加入s[j]的回文子序列长度为dp[i+1] [j]
// (2.2)加入s[i]的回文子序列长度为dp[i] [j-1
//其中dp[i] [j]取最大,即:dp[i] [j] = max(dp[i+1] [j], dp[i] [j-1])
dp[i][j] = max(dp[i+1][j],dp[i][j-1]);
}
}
}
5.距离推导dp数组
输入s:“cbbd” 为例,dp数组状态如图:
红色框为:dp[0] [s.size() - 1]为最终结果
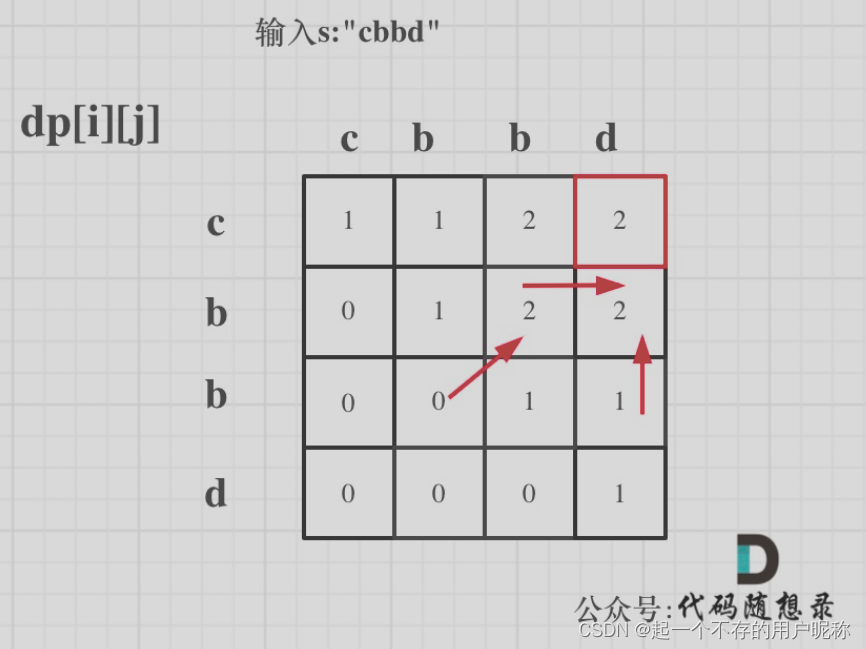
2.3 代码
class Solution {
public:
int longestPalindromeSubseq(string s) {
// 创建一个二维数组,存储每个子串的最长回文子序列的长度
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
// 对角线上的值初始化为1,表示单个字符是一个回文子序列
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
// 外层循环从字符串末尾开始,从后往前遍历所有可能的起点,即子序列的左边界
for (int i = s.size() - 1; i >= 0; i--) {
// 内层循环则从起点的下一个位置开始,遍历到字符串末尾,即子序列的右边界
// 注意,内层循环的起点是i+1,而不是i
for (int j = i + 1; j < s.size(); j++) {
if (s[i] == s[j]) {
// (1)如果s[i]与s[j]相同,那么dp[i] [j] = dp[i+1] [j-1] +2
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
// (2.1)加入s[j]的回文子序列长度为dp[i+1] [j]
// (2.2)加入s[i]的回文子序列长度为dp[i] [j-1
//其中dp[i] [j]取最大,即:dp[i] [j] = max(dp[i+1] [j], dp[i] [j-1])
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
// 返回dp[0][s.size()-1],即整个字符串s的最长回文子序列的长度
return dp[0][s.size() - 1];
}
};
3.参考资料
[代码随想录]