目录

1.单值二叉树

2.相同的树

3.另一棵树的子树

4.反转二叉树

5.对称二叉树

6.二叉树的结构及遍历

扩展：如何判断是不是完全二叉树、二叉树的销毁

1）判断是不是完全二叉树

2）二叉树的销毁

---

1.单值二叉树

OJ题链接https://leetcode.cn/problems/univalued-binary-tree/

 思路：

• 先判断左子树，左子树不为空的情况下，左子树的值不等于根的值，返回false
• 在判断右子树，左子树不为空的情况下，左子树的值不等于根的值，返回false
• 最后如果以上两个条件都不满足，说明左右孩子的值和根的值相同，进行递归调用
  返回该函数的左子树与上右子树

代码：

bool isUnivalTree(struct TreeNode* root)
{
    if(root==NULL)
        return true;
    if(root->left && root->left->val != root->val)
        return false;
    if(root->right && root->right->val != root->val)
        return false;
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

2.相同的树

OJ题链接https://leetcode.cn/problems/same-tree/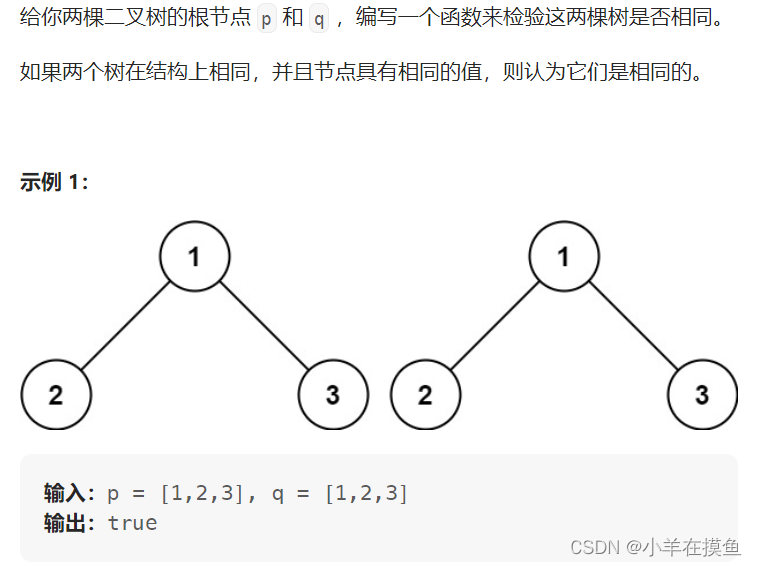

思路：

1. p和q都为空，返回true
2. p和q有一个为空，返回flase
3. p和q都不为空，则判断他们的节点值是否相同，不相同返回false
4. 上面都不满足，进行递归左右节点

注意：

• 第一步和第二步不能互换，
• 不用去管左子树和右子树是否为空的问题，因为递归下去以后就会帮你去判断

代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p==NULL && q==NULL)
        return true;

    if(p==NULL || q==NULL)
        return false;

    if(p->val != q->val)
        return false;
        
    return isSameTree(p->left,q->left) && isSameTree(p->right, q->right);
}

3.另一棵树的子树

OJ题链接https://leetcode.cn/problems/subtree-of-another-tree/

 

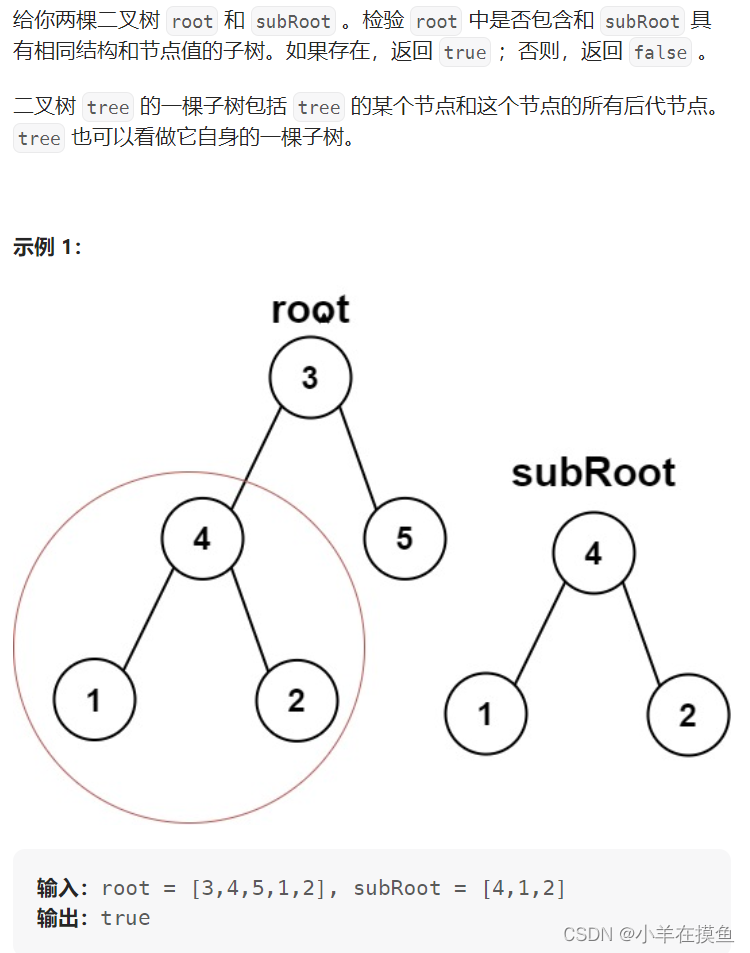
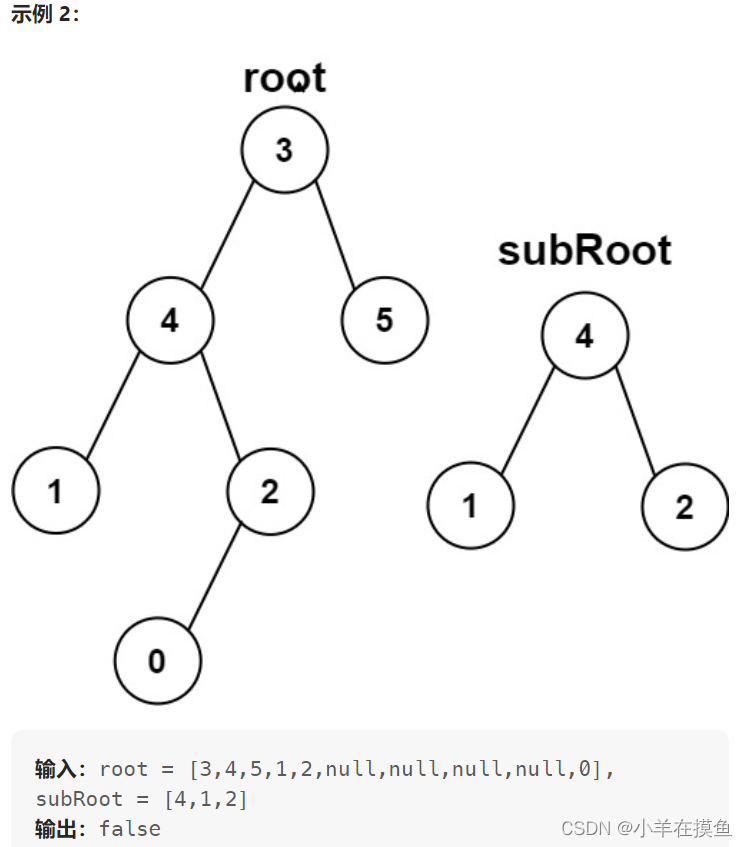
 思路：

• 这道题主要是用root的子树去和subRoot进行比较
• 有了上面判断两个树是否相同的经验，我们只需要递归root来与subRoot比较即可
• 注意递归时使用   ||   （或），在左子树或右子树有一个与subRoot相同的子树即为true

代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p==NULL && q==NULL)
        return true;

    if(p==NULL || q==NULL)
        return false;

    if(p->val != q->val)
        return false;
        
    return isSameTree(p->left,q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(root==NULL)
        return false;

    if(isSameTree(root,subRoot))
        return true;

    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

4.反转二叉树

OJ题链接https://leetcode.cn/problems/binary-tree-preorder-traversal/description/

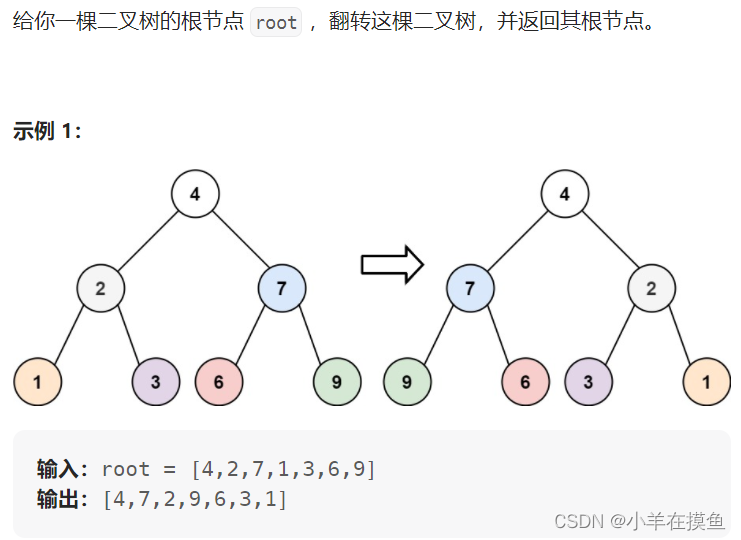
思路：

• 可根据后序遍历的想法，
• 先遍历每一个节点，如果有节点时NULL，直接返回root
• 不为NULL，继续递归遍历左子树，
• 然后再遍历右子树
• 最后将左子树和右子树进行交换

代码：

struct TreeNode* invertTree(struct TreeNode* root)
{
    if(root==NULL)
        return root;
    else
    {
        invertTree(root->left);
        invertTree(root->right);
        struct TreeNode* mp;
        mp=root->left;
        root->left=root->right;
        root->right=mp;
    }
    return root;
}

5.对称二叉树

OJ题链接https://leetcode.cn/problems/symmetric-tree/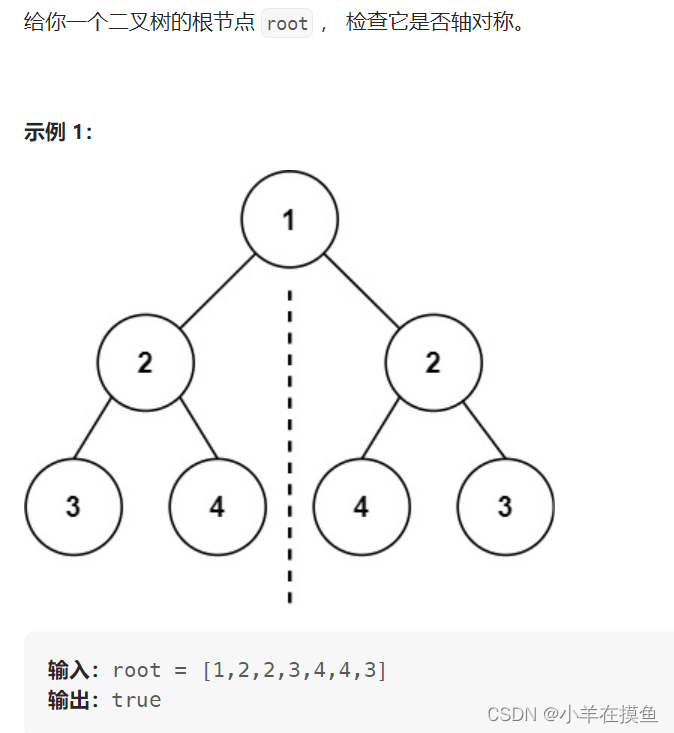

 思路：

• 用左子树的左和右子树的右进行比较，
• 先判断root是否为NULL，
• 建立一个字函数，传左子树的指针和右子树的指针
• 然后判断左子树和右子树是否为NULL，都为NULL返回true，有一个为NULL返回false
• 都不为NULL，继续判断其值是否相同，不相同返回false，
• 相同，继续递归，传递  左的左和右的右 && 左的右和右的左，进行递归

代码：

bool _isSymmetric(struct TreeNode* L,struct TreeNode* R)
{
    if(L->left==NULL && R->right==NULL)
        return true;
    if(L->left==NULL || R->right==NULL)
        return false;
    if(L->val!=R->val)
        return false;
    return _isSymmetric(L->left,R->right) && _isSymmetric(L->right,R->left);
}
bool isSymmetric(struct TreeNode* root)
{
    if(root==NULL)
    {
        return true;
    }
    return _isSymmetric(root->left,root->right);
}

6.二叉树的结构及遍历

OJ题链接https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking

 思路：

看注释理解即可

#include <stdio.h>
#include <stdlib.h>

struct TreeNode
{
    char val;
    struct TreeNode* left;
    struct TreeNode* right;
};

//创建二叉树
struct TreeNode* rebulidTree(char* str, int* i)
{
    //= ‘#’直接返回，并将i++
    if(str[*i]=='#')
    {
        (*i)++;
        return NULL;
    }
    //不为‘#’首先malloc一个新的节点，并让root->val指向数组中对应下标位置的值
    struct TreeNode* root=(struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->val = str[(*i)++];
    
    //递归左子树和右子树
    root->left = rebulidTree(str, i);
    root->right = rebulidTree(str, i);

    return root;
}

//中序遍历
void InOrder(struct TreeNode* root)
{
    if(root==NULL)
        return;
    InOrder(root->left);
    printf("%c ",root->val);
    InOrder(root->right);

}

int main() 
{
    char str[100];
    scanf("%s",str);

    int i=0;
    //这里传参一定一定要传地址，因为在递归过程中虽然i++过了，
    //但只是在局部的栈帧中，返回之后栈帧销毁，i还是不会变的
    struct TreeNode* root = rebulidTree(str,&i);

    InOrder(root);

    return 0;
}

扩展：如何判断是不是完全二叉树、二叉树的销毁

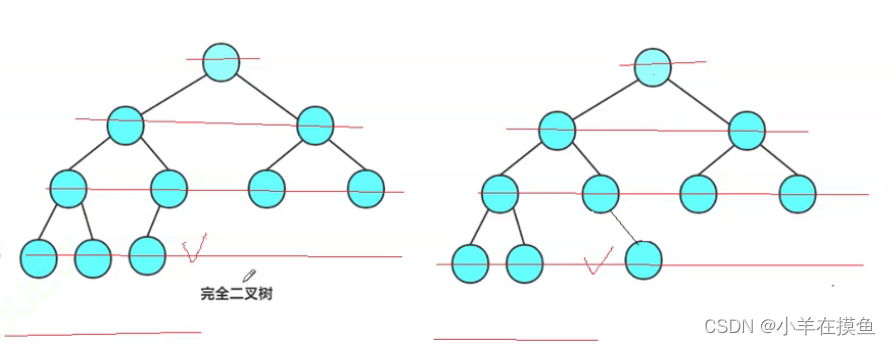
1）判断是不是完全二叉树

思路：

• 和层序遍历的思想一样，利用队列的先进先出进行
• 如果是完全二叉树，在出队列，出到NULL时，队列后面的元素应全为空

• 如果不是完全二叉树，在出队列，出到NULL时，队列后面的元素会有不为空的情况

• 我们可以加入一个flag做个判断标志，在第一次遇到NULL是，将flag变为false

• 在只会再遇到不为空的元素时，如果flag为false，直接返回false

 代码如下：

//判断二叉树是否为完全二叉树：
bool isCompleteTree(BTNode* root)
{
	BTNode* queue[1000];  //直接用树的结构来生成一个队列（只用到data变量，不用到左右孩子）

	int head = 0, tail = 0;    //head即队列的头节点，用来出数据，tail即队列的尾结点，用来入数据

	bool flag = false;      // 存储是否出现过空节点的标记

	queue[tail++] = root;   //先让队列的头=树的根节点

	while (head < tail) 
	{
		BTNode* curNode = queue[head++];
		
		//在第一次遇到NULL的时候，用flag进行记录
		if (curNode == NULL)
			flag = true;
		else 
		{
			if (flag)        // 如果之前出现过空节点，说明当前节点不是完全二叉树的节点
				return false;
			queue[tail++] = curNode->left;
			queue[tail++] = curNode->right;
		}
	}
	return true;
}

2）二叉树的销毁

思路：递归进行销毁，和后序遍历类似

void destroyTree(BTNode* root)
{
	if (root == NULL)
		return;
	destroyTree(root->left);
	destroyTree(root->right);
	free(root);
}