目录
一.数论
1.质数
(1)质数的判断
(2)分解质因数(数=几个质数相乘)
(3)求1-n的所有质数
2.约数
(1)试除法求所有约数
(2)约数个数和约数之和
(3)最大公约数(欧几里得算法 )
一.数论
1.质数
在大于1 的整数,只包含1和本身这两个约数,则称为质数(素数) 2 3 5 7 11 13 17
(1)质数的判断
试除法(优化)枚举到根号x O(根号x)
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ ) //以前是i<x
if (x % i == 0) //包含其他约数
return false;
return true;
}(2)分解质因数(数=几个质数相乘)
void divide(int x)
{
for (int i = 2; i <= x / i; i ++ ) //x/i即sqrt复杂度
if (x % i == 0) //i一定是质数
{
int s = 0; //计数
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}
//eg
//x=6
// 2 1
// 3 1
//x=3
// 3 1 这里用到了x>1语句,因为直接跳出for循环x/i,只能另外判断(3)求1-n的所有质数
埃式筛法O(nloglogn)
先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个素数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个素数5筛,把5留下,把5的倍数剔除掉;不断重复下去…。
如图:
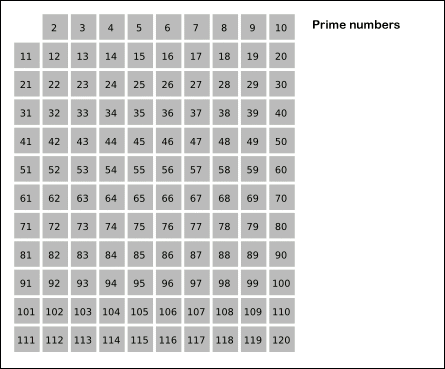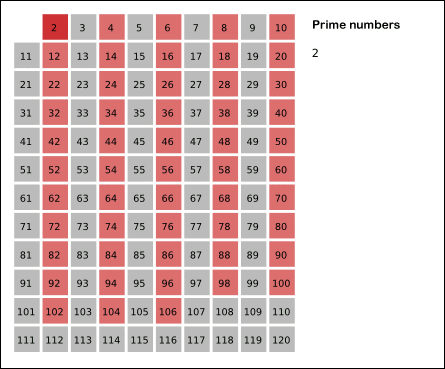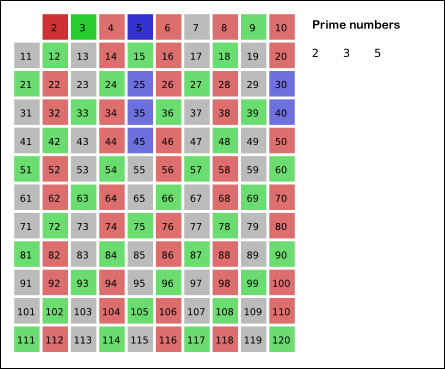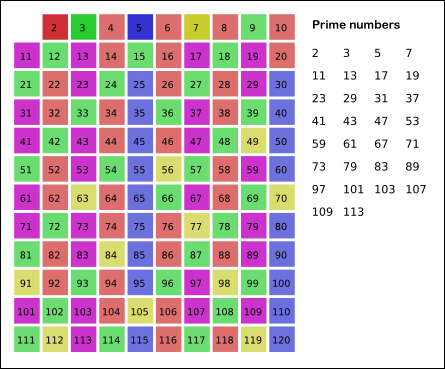
算法核心:把每个质数的所有倍数筛掉
int primes[N], cnt; // primes[]存储所有素数
bool st[N]; // st[x]存储x是否被筛掉 默认false
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (st[i]) continue; //st如果是true 说明被筛过,那么它的倍数肯定被筛过,所以直接跳过
//接下来对该质数的所有倍数进行筛选
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
2.约数
什么是约数?
约数,又称因数。整数a除以整数b(b≠0),除得的商正好是整数而没有余数,我们就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。
(1)试除法求所有约数
暴力来解决这个问题很简单,就是从1开始遍历到n即可
for(int i = 1; i <= x; i++)
{
if(x % i == 0) res.push_back(i);
}通过对质数的学习,我们知道一个数的因数即约数是成对出现的,所以我们同样可以用试除法,计算小的约数,并将大的约数添加到答案里,注意判断一下两者是否相同避免重复即可。
for(int i = 1; i <= x / i; i++)
if(x % i == 0)
{
res.push_back(i);
if(i != x/i) res.push_back(x/i);
} 给定 n 个正整数 ai,对于每个整数 ai,请你按照从小到大的顺序输出它的所有约数。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个整数 ai。
输出格式
输出共 n 行,其中第 i 行输出第 i 个整数 ai 的所有约数。
数据范围
1≤n≤100,
2≤ai≤2×1e9
输入样例:
2
6
8
输出样例:
1 2 3 6
1 2 4 8 #include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int n;
int main()
{
cin>>n;
while(n--)
{
int x;
cin >> x;
vector<int> res;
for(int i = 1; i <= x / i; i++)
if(x % i == 0)
{
res.push_back(i);
if(i != x/i) res.push_back(x/i);
}
sort(res.begin(), res.end());
for (auto k : res) cout << k << ' ';
cout << endl;
}
return 0;
}
(2)约数个数和约数之和
如果一个数N分解质因数为 N = p1^c1 * p2^c2 * ... *pk^ck (p为质数)
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
example 36=2*2*3*3=2^2 * 3^2
36的约数为 2^0*3^0 2^0*3^1 2^0*3^2 2^1*3^0 2^1*3^1 …………2^2*3^2
只需改变质因数的个数,就会多一个约束
一共(2+1)(2+1)= 9种
代码实现的思路:
1、在每次输入一个数时,分解其质因数,将其出现的次数保存起来;
2、遍历保存质因数的表,将每个质因数出现的次数+1再相乘即可(即约数个数公式)。
#include<iostream>
#include<algorithm>
#include<unordered_map>
#include<vector>
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9+7;
int main(){
int n;
cin >> n;
unordered_map<int,int> primes;
// 每次将输入的数分解质因数,质因数放在primes中
while (n -- )
{
int x;
cin >> x;
for (int i = 2; i <= x / i; i ++ ) // 分解质因数
while (x % i == 0)
{
x /= i;
primes[i] ++ ;
}
if (x > 1) primes[x] ++ ; // 保存最后一个质因数
}
LL res = 1;
for(auto p : primes) res = res*(p.second+1) % mod;
cout << res << endl;
return 0;
}
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)
对于约数个数那个式子,它所选取的括号里的每一个p也是不同的,即分解后的每一个乘积式子都可以看作一个数,这样我们就将所有约数的和求出了。
//约数之和,则只用改这个for循环即可
for (auto prime : primes)
{
LL p = prime.first, a = prime.second;
LL t = 1;
while (a--) t = (t * p + 1) % mod;
//还要算0次方,算0次方就直接加1了,然后从一次方算方便些
/*计算一下:
第一步:
t = (t * a + 1)
t=p1的一次方+p1的零次方;
第二步:
t = (t * a + 1)
t=p1的二次方+p1的一次方+1=p1的二次方+p1的一次方+p1的零次方;
*/
res = res * t % mod;
}
(3)最大公约数(欧几里得算法 )
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}