Direct3D 12——灯光—

Direct3D 12——灯光——聚光灯光

news2024/9/28 17:26:16

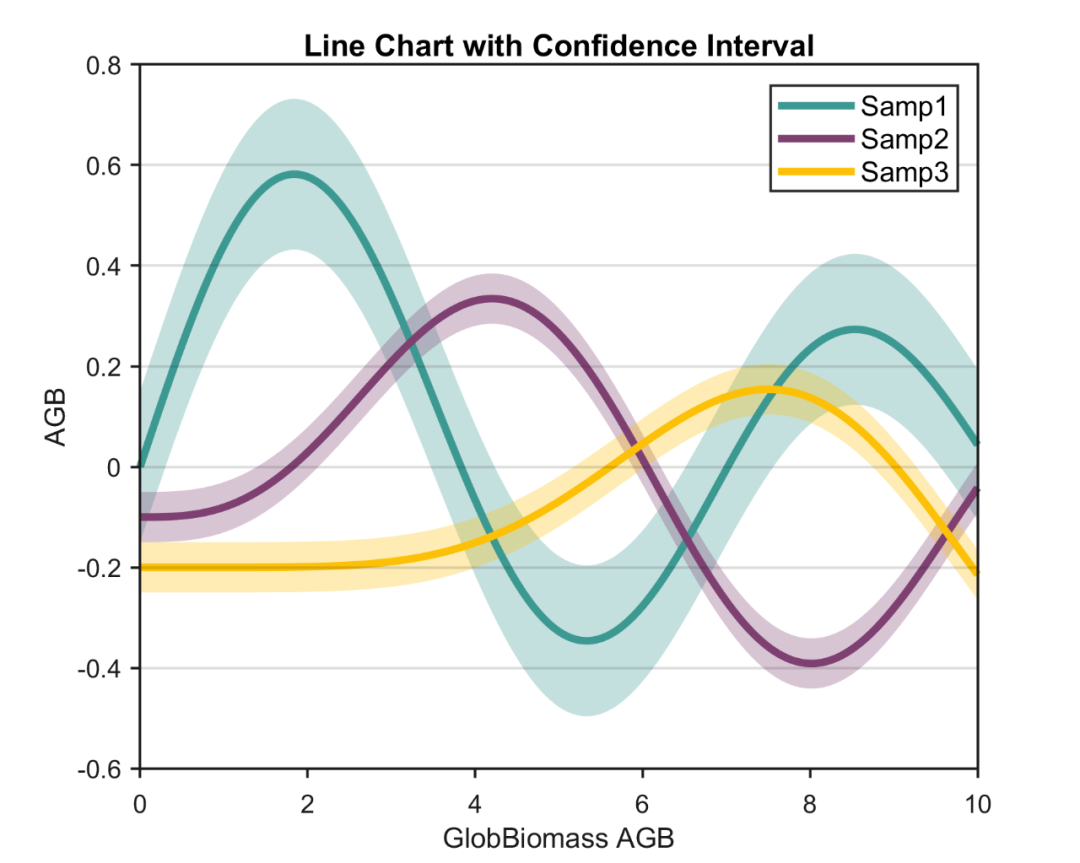
一个与聚光灯光源（spotlight）相近的现实实例是手电筒。从本质上来说，聚光灯由位置Q向方向d 照射出范围呈圆锥体的光。
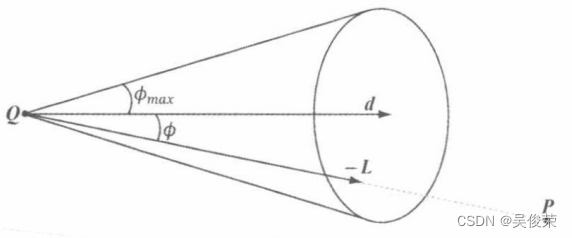
在这里插入图片描述
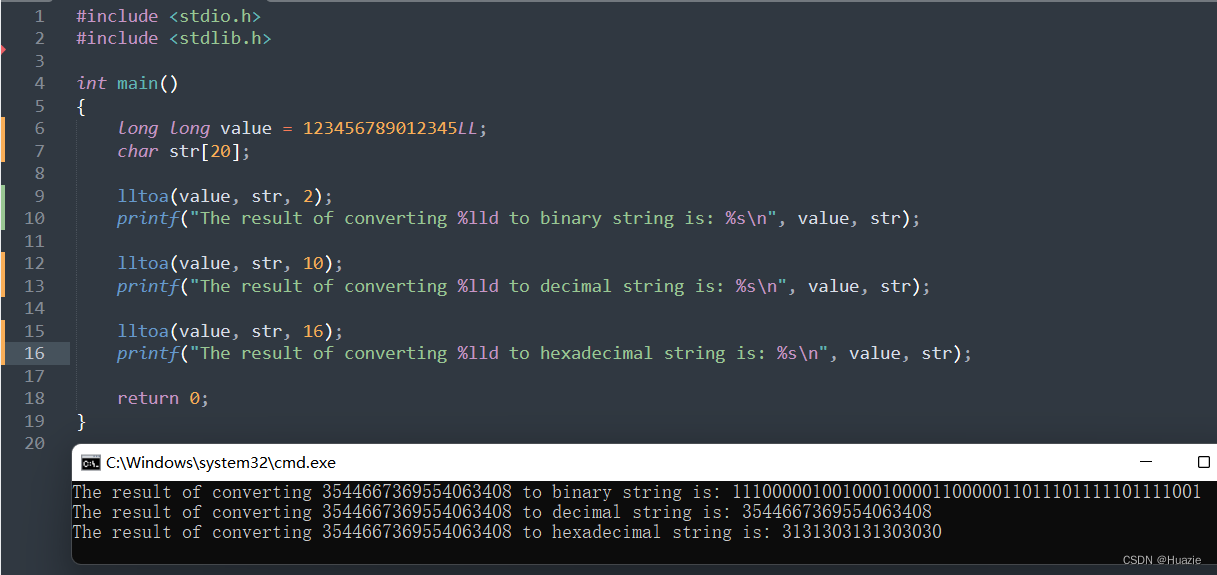
一个聚光灯以位置Q向方向d发射出半顶角为Φmax 的圆锥体范围的光

其中，P为被照点的位置，Q是聚光灯的位置。观察图可知，当且仅当位于 -L 与 d 之间的夹角。小于圆锥体的半顶角Φmax时，P才位于聚光灯的圆锥体范围之中（所以它才可以被光照射到）。而且，聚光灯圆锥体范围内所有光线的强度也不尽相同。位于圆锥体中心处的光线（即Qd这条向量上的光线）光强应该是最强的，而随着角Φ由 0 增加至Φmax ,光强会逐渐趋近于0。
那么，怎样用与Φ相关的函数来控制光强的衰减我们可以使用与图中曲线相同的函数，但是要以Φ替换θh ,再用s代替m：

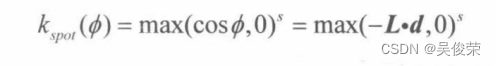
在这里插入图片描述
这正是我们所期待的公式：光强随着Φ的增加而连续且平滑地衰减。另外，通过修改幕、s,我们就能够间接地控制Φmax（使光强降为0的半顶角角度）。也就是说，我们可以通过设置不同的s值来缩小或扩大聚光灯光源的圆锥体照射范围。例如，如果设s = 8,则圆锥体的半顶角就逼近45。
将光源的直射光量与衰减因子相乘之后，还要根据被照射点位于聚光灯圆锥体的具体位置, 用聚光灯因子kspot按比例对光强进行缩放。

实现

//实现了一种线性衰减因子的计算方法，可将其应用于点光源于聚光灯
float CalcAttenuation(float d, float falloffStart, float falloffEnd)
{
    // Linear falloff.
    return saturate((falloffEnd-d) / (falloffEnd - falloffStart));
}

//代替菲涅尔方程的石里克近似。此函数基于光向量L于表面法线n之间的夹角，并根据菲涅尔效应近似地计算出以n为法线的表面所反射光的百分比
// Schlick gives an approximation to Fresnel reflectance (see pg. 233 "Real-Time Rendering 3rd Ed.").
// R0 = ( (n-1)/(n+1) )^2, where n is the index of refraction.
float3 SchlickFresnel(float3 R0, float3 normal, float3 lightVec)
{
    float cosIncidentAngle = saturate(dot(normal, lightVec));

    float f0 = 1.0f - cosIncidentAngle;
    float3 reflectPercent = R0 + (1.0f - R0)*(f0*f0*f0*f0*f0);

    return reflectPercent;
}

//计算反射到观察者眼中的光量，该值为漫反射光量于镜面反射光量的总和
float3 BlinnPhong(float3 lightStrength, float3 lightVec, float3 normal, float3 toEye, Material mat)
{
    //m由光泽度推导而来，而光泽度则根据粗糙度求得
    const float m = mat.Shininess * 256.0f;
    float3 halfVec = normalize(toEye + lightVec);

    float roughnessFactor = (m + 8.0f)*pow(max(dot(halfVec, normal), 0.0f), m) / 8.0f;
    float3 fresnelFactor = SchlickFresnel(mat.FresnelR0, halfVec, lightVec);

    float3 specAlbedo = fresnelFactor*roughnessFactor;

    //尽管我们进行的是LDR（low dynamic range .低动态范围）渲染，但spec（镜面反射）公式得到
    // 的结果仍会超出范围[0,1],因此现将其按比例缩小一些
    // Our spec formula goes outside [0,1] range, but we are 
    // doing LDR rendering.  So scale it down a bit.
    specAlbedo = specAlbedo / (specAlbedo + 1.0f);

    return (mat.DiffuseAlbedo.rgb + specAlbedo) * lightStrength;
}

//聚光灯
float3 ComputeSpotLight(Light L, Material mat, float3 pos, float3 normal, float3 toEye)
{
    //从表面指向光源的向量
    // The vector from the surface to the light.
    float3 lightVec = L.Position - pos;

    //由表面到光源的距离
    // The distance from surface to light.
    float d = length(lightVec);

    //范围检测
    // Range test.
    if(d > L.FalloffEnd)
        return 0.0f;

    //对光向量进行规范化处理
    // Normalize the light vector.
    lightVec /= d;

    //通过朗伯余弦定律按比例缩小光的强度
    // Scale light down by Lambert's cosine law.
    float ndotl = max(dot(lightVec, normal), 0.0f);
    float3 lightStrength = L.Strength * ndotl;

    //根据距离计算光的衰减
    // Attenuate light by distance.
    float att = CalcAttenuation(d, L.FalloffStart, L.FalloffEnd);
    lightStrength *= att;

    //根据聚光灯照明模型对光强进行缩放处理
    // Scale by spotlight
    float spotFactor = pow(max(dot(-lightVec, L.Direction), 0.0f), L.SpotPower);
    lightStrength *= spotFactor;

    return BlinnPhong(lightStrength, lightVec, normal, toEye, mat);
}