1 Yolov5四种网络模型
Yolov5官方代码中,给出的目标检测网络中一共有4个版本,分别是Yolov5s、Yolov5m、Yolov5l、Yolov5x四个模型。
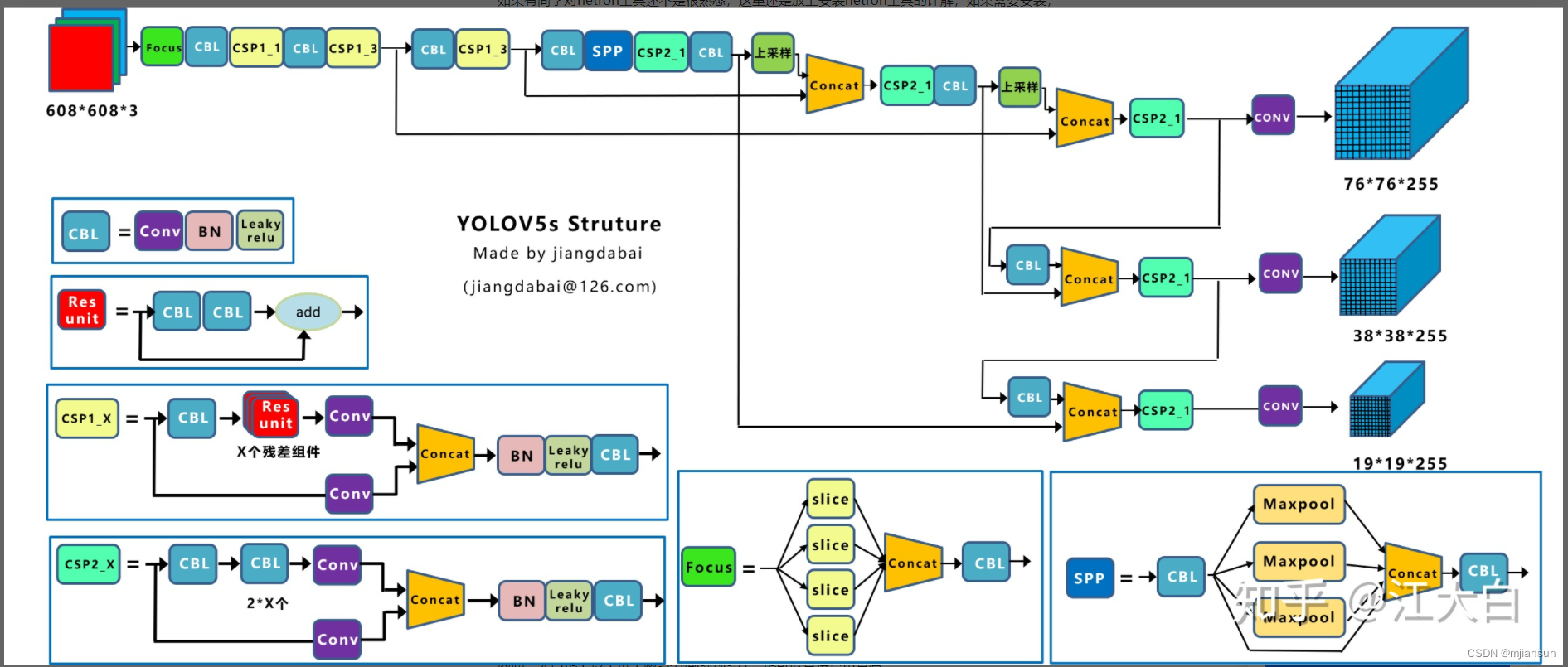
1.1Yolov5网络结构图
eg:Yolov5s
2.1 Yolov3&Yolov4网络结构图
2.1.1 Yolov3网络结构图
Yolov3的网络结构是比较经典的one-stage结构,分为输入端、Backbone、Neck和Prediction四个部分
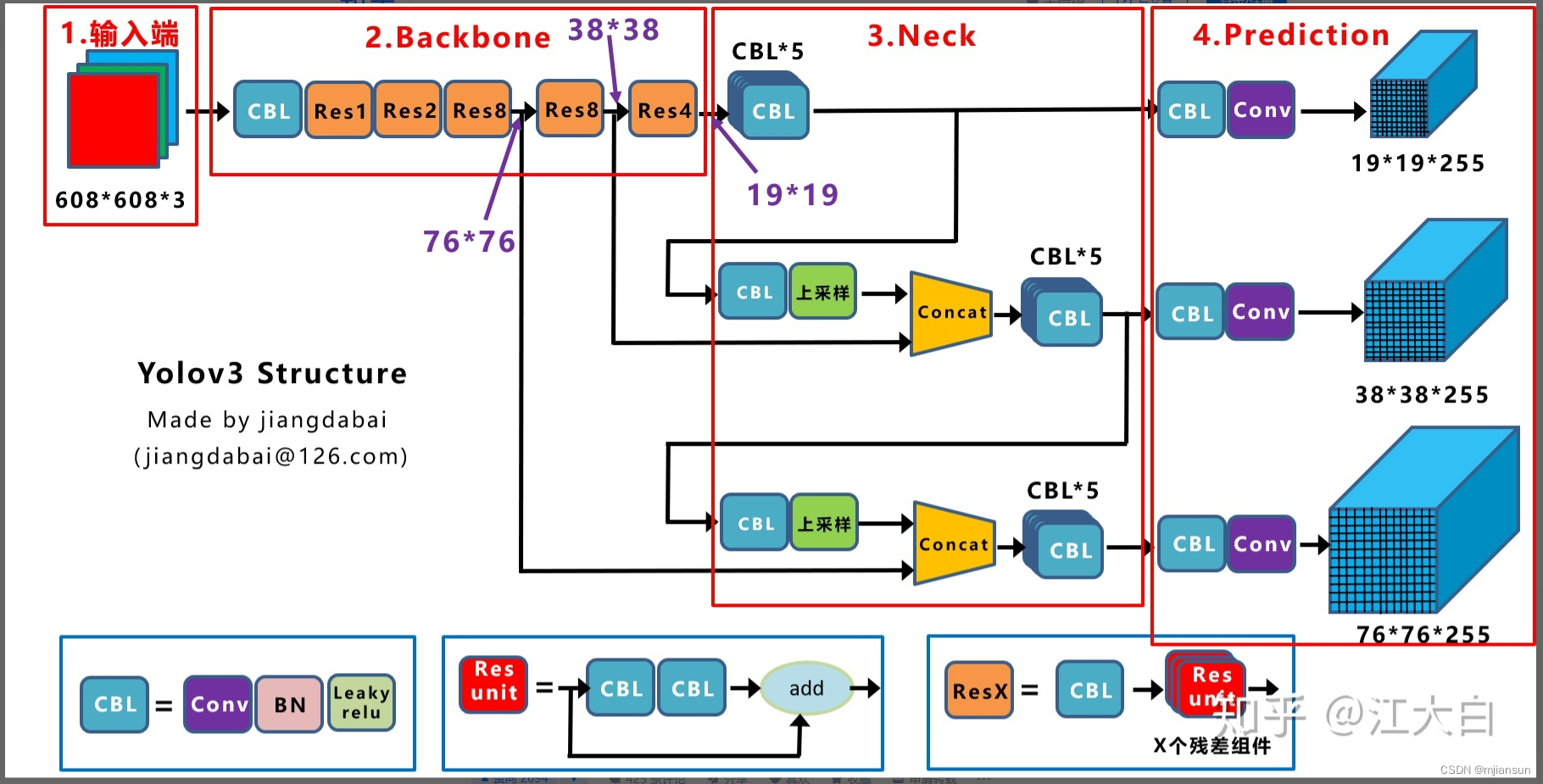
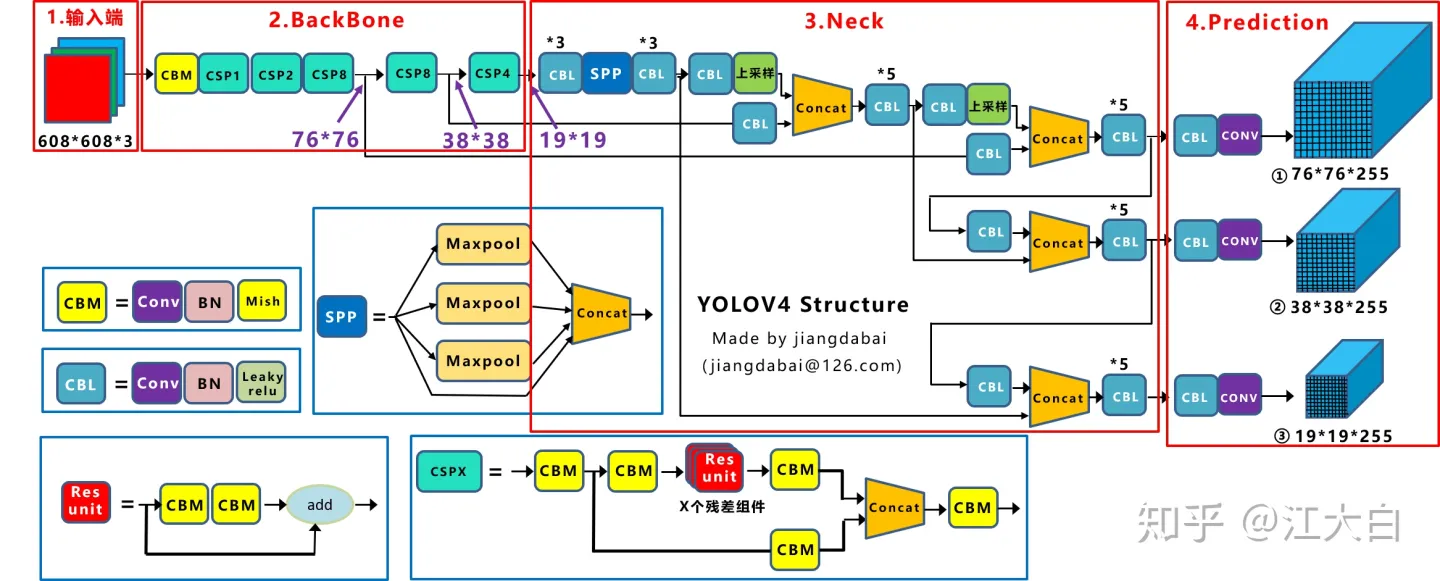
2.1.2 Yolov4网络结构图
Yolov4在Yolov3的基础上进行了很多的创新。
比如:
输入端,主要包括Mosaic数据增强、cmBN、SAT自对抗训练
Backbone主干网络上采用了CSPDarknet53、Mish激活函数、Dropblock等方式,
Neck中采用了SPP、FPN+PAN的结构,
输出端损失函数CIOU_Loss,以及预测框筛选的nms变为DIOU_nms
2.2 Yolov5核心基础内容
还是分为输入端、Backbone、Neck、Prediction四个部分。
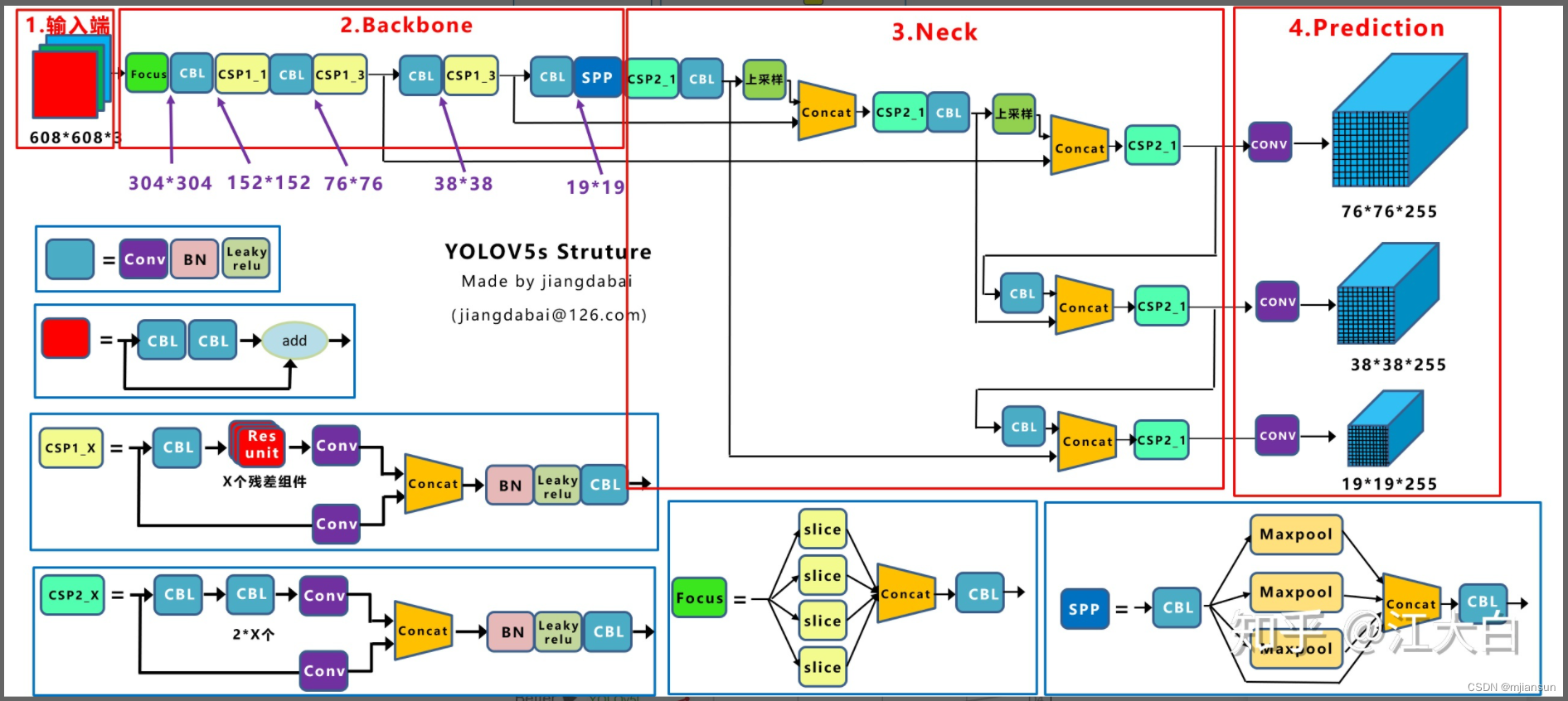
列举它和Yolov3的一些主要的不同点,并和Yolov4进行比较。主要的不同点:
(1)输入端:Mosaic数据增强、自适应锚框计算、自适应图片缩放
(2)Backbone:Focus结构,CSP结构
(3)Neck:FPN+PAN结构
(4)Prediction:GIOU_Loss
Yolov5作者的算法性能测试图
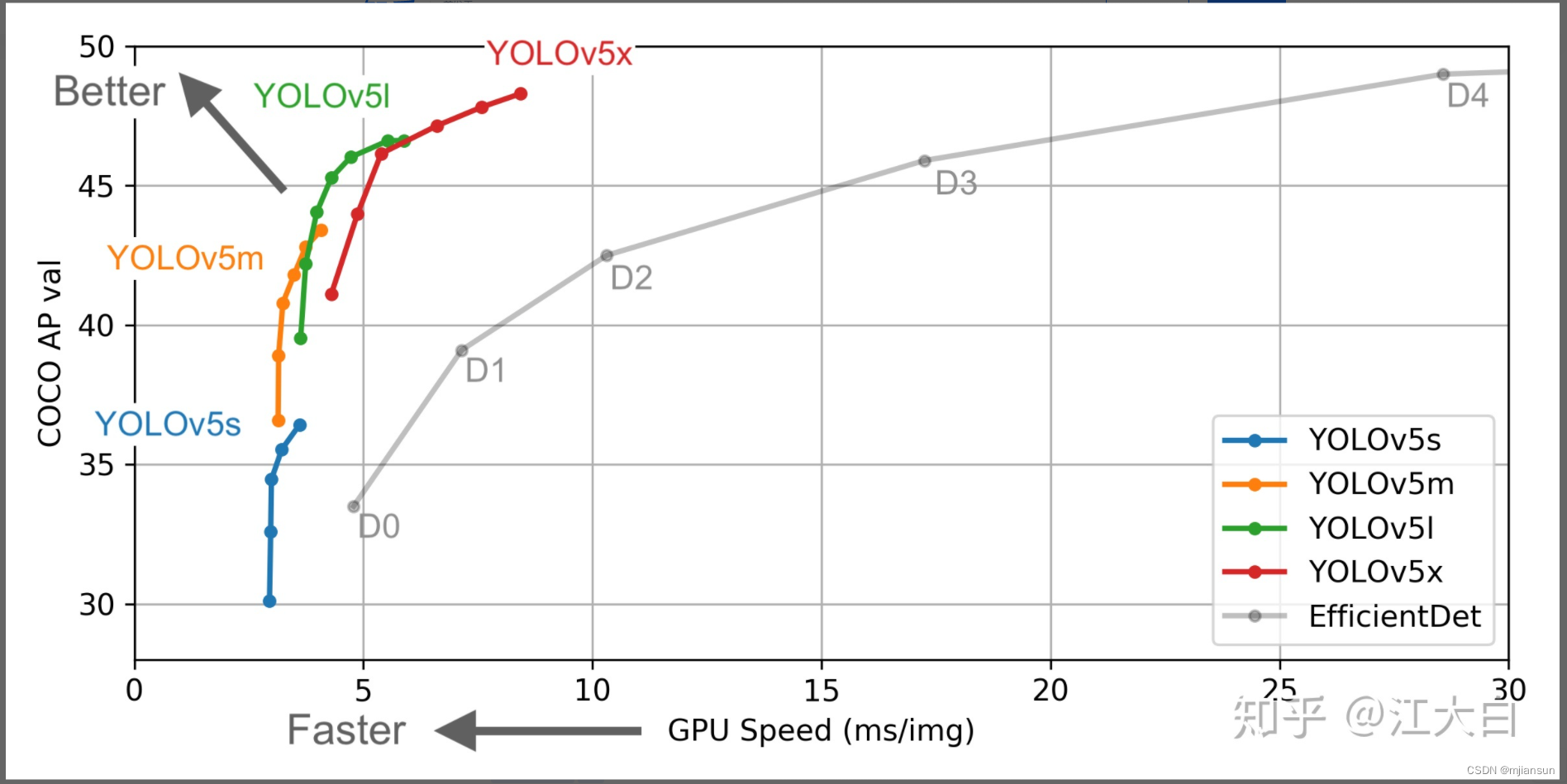
Yolov5s网络最小,速度最少,AP精度也最低。但如果检测的以大目标为主,追求速度,倒也是个不错的选择。
2.2.1 输入端
1)Mosaic数据增强
Yolov5的输入端采用了和Yolov4一样的Mosaic数据增强的方式。
Mosaic数据增强采用了4张图片,随机缩放、随机裁剪、随机排布的方式进行拼接,对于小目标的检测效果还是很不错的。
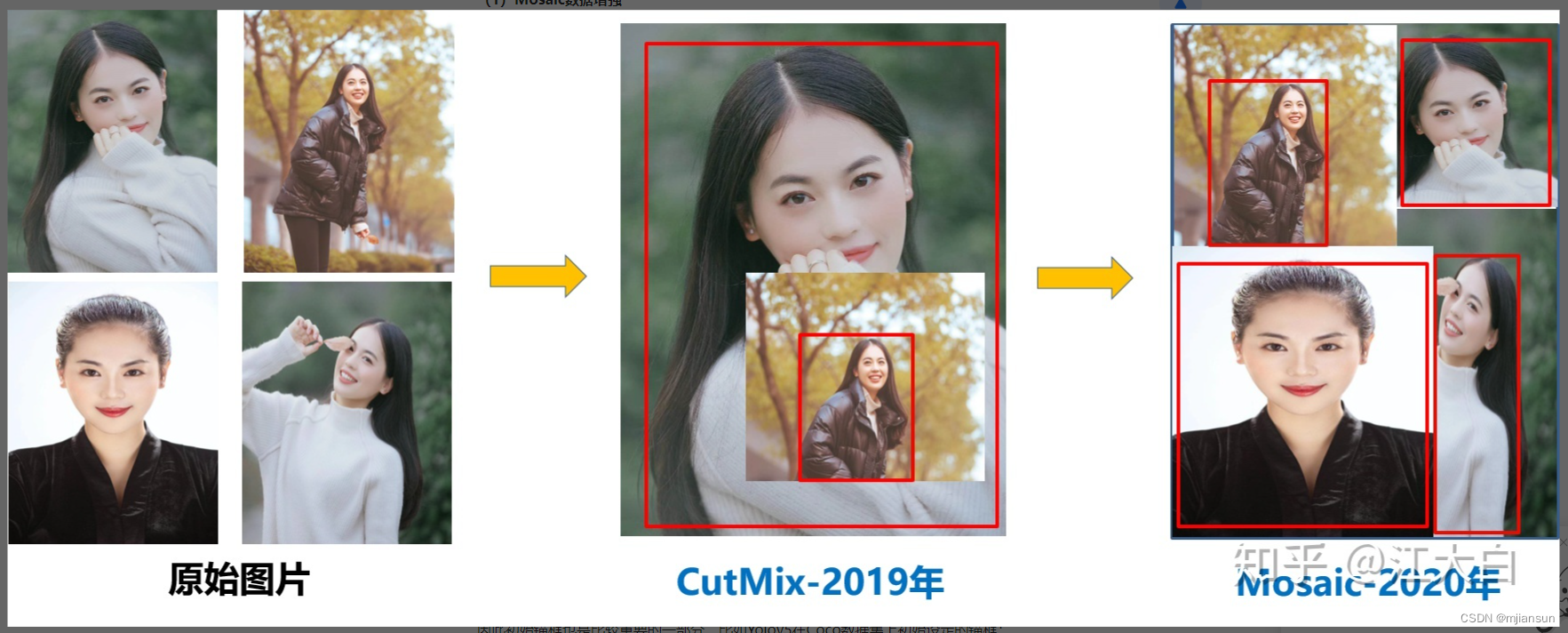
为什么要进行Mosaic数据增强呢?
在平时项目训练时,小目标的AP一般比中目标和大目标低很多。而Coco数据集中也包含大量的小目标,但比较麻烦的是小目标的分布并不均匀。
首先看下小、中、大目标的定义:

可以看到小目标的定义是目标框的长宽0×0~32×32之间的物体。
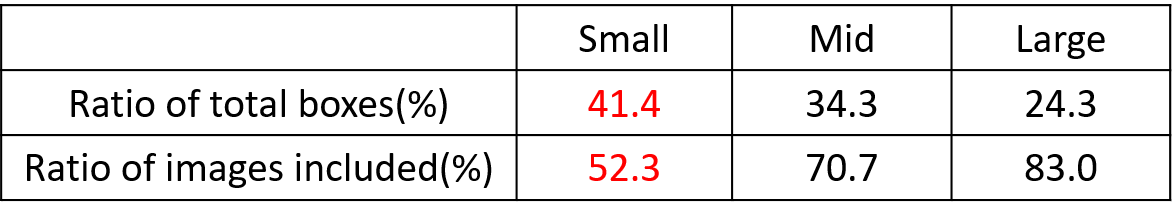 但在整体的数据集中,小、中、大目标的占比并不均衡。
但在整体的数据集中,小、中、大目标的占比并不均衡。
如上表所示,Coco数据集中小目标占比达到41.4%,数量比中目标和大目标都要多。
但在所有的训练集图片中,只有52.3%的图片有小目标,而中目标和大目标的分布相对来说更加均匀一些。
主要有几个优点:
- **丰富数据集:**随机使用4张图片,随机缩放,再随机分布进行拼接,大大丰富了检测数据集,特别是随机缩放增加了很多小目标.
- **减少GPU:**可能会有人说,随机缩放,普通的数据增强也可以做,但作者考虑到很多人可能只有一个GPU,因此Mosaic增强训练时,可以直接计算4张图片的数据,使得Mini-batch大小并不需要很大,一个GPU就可以达到比较好的效果。
(2) 自适应锚框计算
在Yolo算法中,针对不同的数据集,都会有初始设定长宽的锚框。
在网络训练中,网络在初始锚框的基础上输出预测框,进而和真实框groundtruth进行比对,计算两者差距,再反向更新,迭代网络参数。
因此初始锚框也是比较重要的一部分,比如Yolov5在Coco数据集上初始设定的锚框:

在Yolov3、Yolov4中,训练不同的数据集时,计算初始锚框的值是通过单独的程序运行的。
但Yolov5中将此功能嵌入到代码中,每次训练时,自适应的计算不同训练集中的最佳锚框值。
当然,如果觉得计算的锚框效果不是很好,也可以在代码中将自动计算锚框功能关闭。

控制的代码即train.py中上面一行代码,设置成False,每次训练时,不会自动计算。
(3)自适应图片缩放
在常用的目标检测算法中,不同的图片长宽都不相同,因此常用的方式是将原始图片统一缩放到一个标准尺寸,再送入检测网络中。
比如Yolo算法中常用416416,608608等尺寸,比如对下面800*600的图像进行缩放。

作者认为,在项目实际使用时,很多图片的长宽比不同,因此缩放填充后,两端的黑边大小都不同,而如果填充的比较多,则存在信息冗余,影响推理速度。
因此在Yolov5的代码中datasets.py的letterbox函数中进行了修改,对原始图像自适应的添加最少的黑边。
图像高度上两端的黑边变少了,在推理时,计算量也会减少,即目标检测速度会得到提升。通过这种简单的改进,推理速度得到了37%的提升,可以说效果很明显。
计算步骤:(在datasets.py的letterbox函数中有详细的代码)
第一步:计算缩放比例
 原始缩放尺寸是416*416,都除以原始图像的尺寸后,可以得到0.52,和0.69两个缩放系数,选择小的缩放系数。
原始缩放尺寸是416*416,都除以原始图像的尺寸后,可以得到0.52,和0.69两个缩放系数,选择小的缩放系数。
第二步:计算缩放后的尺寸

原始图片的长宽都乘以最小的缩放系数0.52,宽变成了416,而高变成了312。
第三步:计算黑边填充数值

将416-312=104,得到原本需要填充的高度。再采用numpy中np.mod取余数的方式,得到8个像素,再除以2,即得到图片高度两端需要填充的数值。
**为什么np.mod函数的后面用32?**因为Yolov5的网络经过5次下采样,而2的5次方,等于32。所以至少要去掉32的倍数,再进行取余
此外,需要注意的是:
a.这里填充的是黑色,即(0,0,0),而Yolov5中填充的是灰色,即(114,114,114),都是一样的效果。
b.训练时没有采用缩减黑边的方式,还是采用传统填充的方式,即缩放到416*416大小。只是在测试,使用模型推理时,才采用缩减黑边的方式,提高目标检测,推理的速度。
2.2.2 Backbone
(1)Focus结构
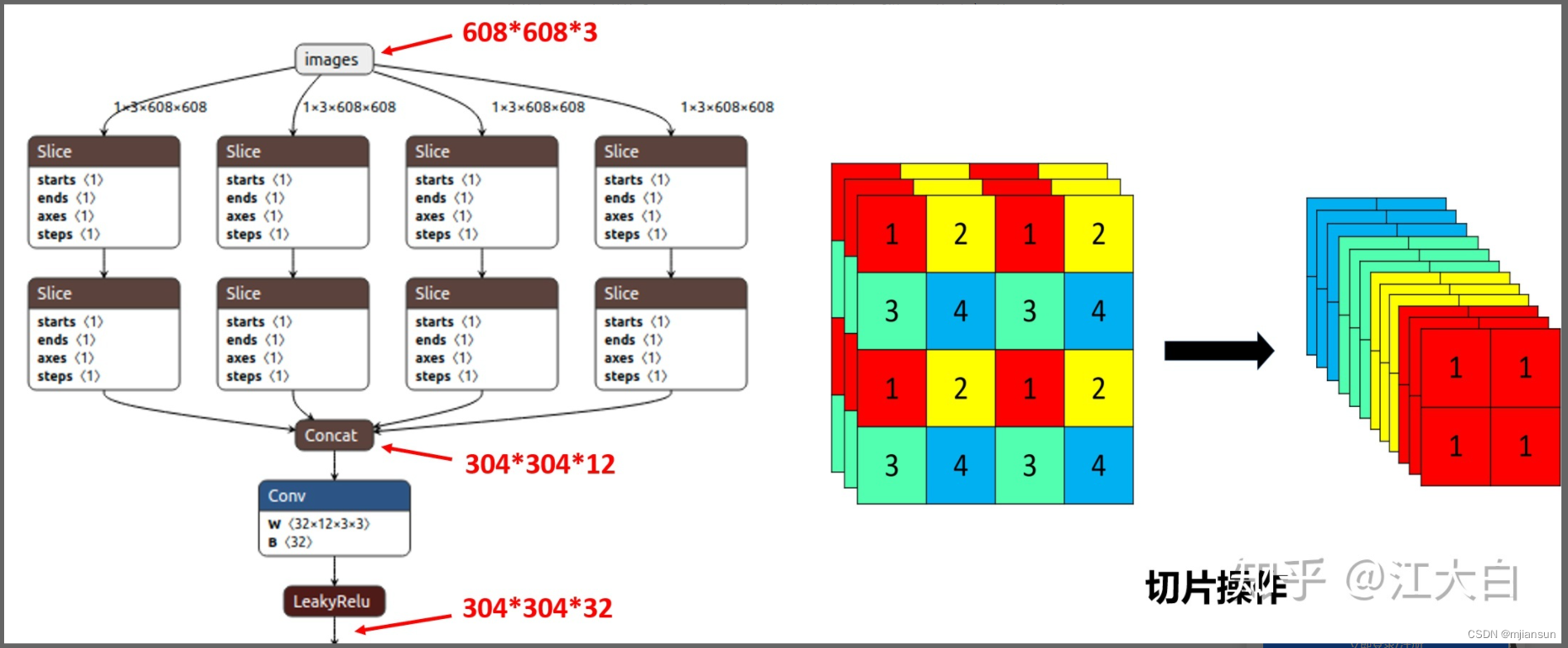
Focus结构,在Yolov3&Yolov4中并没有这个结构,其中比较关键是切片操作。
比如右图的切片示意图,443的图像切片后变成2212的特征图。(一张图切4片)
以Yolov5s的结构为例,原始6086083的图像输入Focus结构,采用切片操作,先变成30430412的特征图,再经过一次32个卷积核的卷积操作,最终变成30430432的特征图。
需要注意的是:Yolov5s的Focus结构最后使用了32个卷积核,而其他三种结构,使用的数量有所增加,先注意下,后面会讲解到四种结构的不同点。
(2)CSP结构
Yolov4网络结构中,借鉴了CSPNet的设计思路,在主干网络中设计了CSP结构。

每个CSP模块前面的卷积核的大小都是3*3,stride=2,因此可以起到下采样的作用。
因为Backbone有5个CSP模块,输入图像是608*608,所以特征图变化的规律是:608->304->152->76->38->19
经过5次CSP模块后得到19*19大小的特征图。
CSP主要有三个方面的优点:
优点一:增强CNN的学习能力,使得在轻量化的同时保持准确性。
优点二:降低计算瓶颈
优点三:降低内存成本
Yolov5与Yolov4不同点在于,Yolov4中只有主干网络使用了CSP结构。
而Yolov5中设计了两种CSP结构,以Yolov5s网络为例,CSP1_X结构应用于Backbone主干网络,另一种CSP2_X结构则应用于Neck中。

2.2.3 Neck
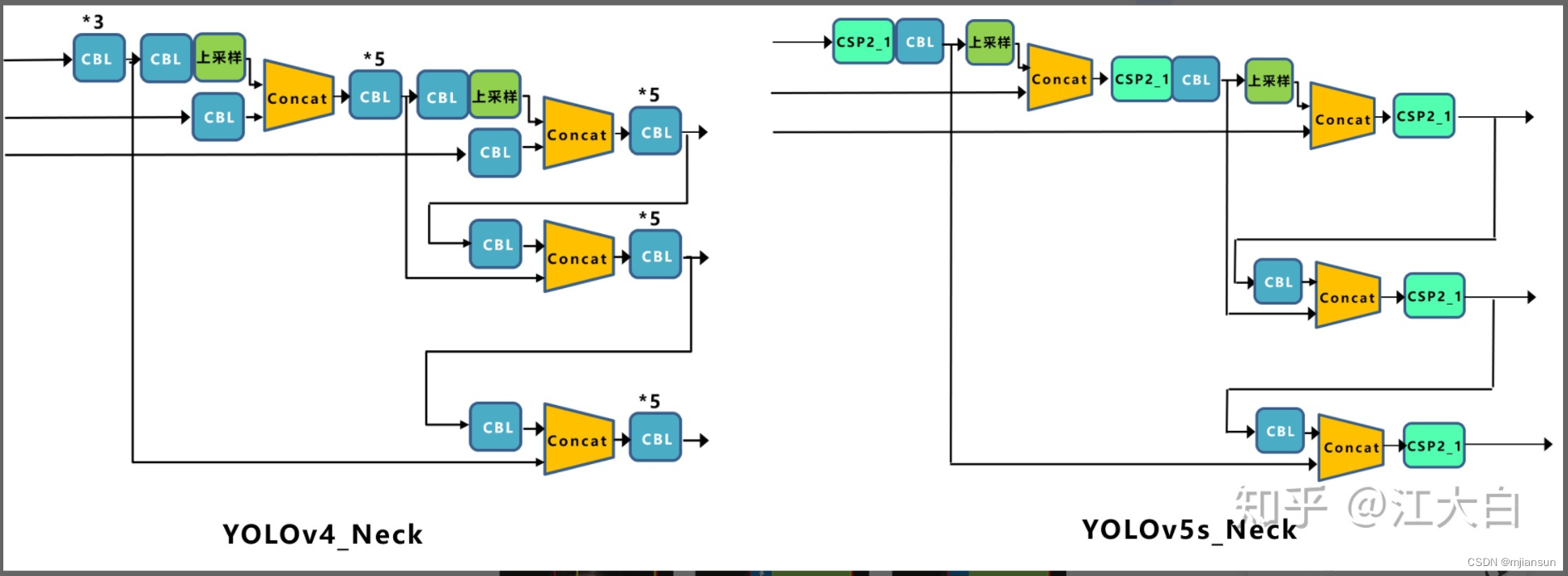
Yolov5现在的Neck和Yolov4中一样,都采用FPN+PAN的结构,但在Yolov5刚出来时,只使用了FPN结构,后面才增加了PAN结构,此外网络中其他部分也进行了调整。
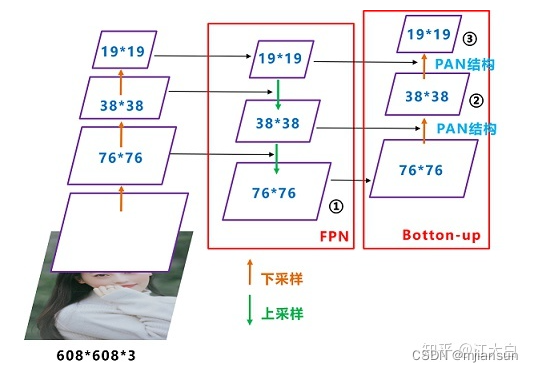
Yolov5和Yolov4的不同点在于,
- Yolov4的Neck结构中,采用的都是普通的卷积操作。
- 而Yolov5的Neck结构中,采用借鉴CSPnet设计的CSP2结构,加强网络特征融合的能力。
2.2.4 输出端
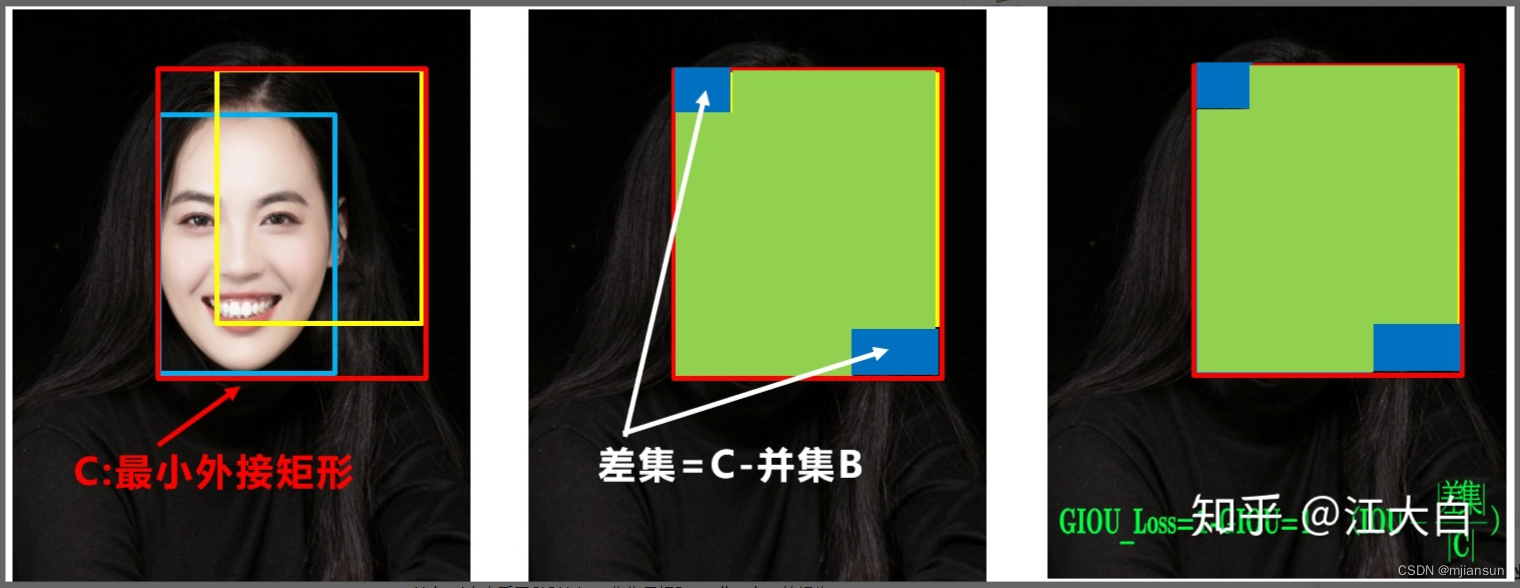
(1)Bounding box损失函数
Yolov5中采用CIOU_Loss做Bounding box的损失函数。
目标检测任务的损失函数一般由Classificition Loss(分类损失函数)和Bounding Box Regeression Loss(回归损失函数)两部分构成。
(2)nms非极大值抑制
在目标检测的后处理过程中,针对很多目标框的筛选,通常需要nms操作。
因为CIOU_Loss中包含影响因子v,涉及groudtruth的信息,而测试推理时,是没有groundtruth的。
所以Yolov4在DIOU_Loss的基础上采用DIOU_nms的方式,而Yolov5中采用加权nms的方式。
可以看出,采用DIOU_nms,下方中间箭头的黄色部分,原本被遮挡的摩托车也可以检出。

2.3 Yolov5四种网络结构的不同点
2.3.1 四种结构的参数
先取出Yolov5代码中,每个网络结构的两个参数:

四种结构就是通过上面的两个参数,来进行控制网络的深度和宽度。其中depth_multiple控制网络的深度,width_multiple控制网络的宽度。
2.3.2 Yolov5网络结构
四种结构的yaml文件中,下方的网络架构代码都是一样的。
为了便于讲解,将其中的Backbone部分提取出来,讲解如何控制网络的宽度和深度,yaml文件中的Head部分也是同样的原理。

在对网络结构进行解析时,yolo.py中下方的这一行代码将四种结构的depth_multiple,width_multiple提取出,赋值给gd,gw。后面主要对这gd,gw这两个参数进行讲解。

2.3.3 Yolov5四种网络的深度
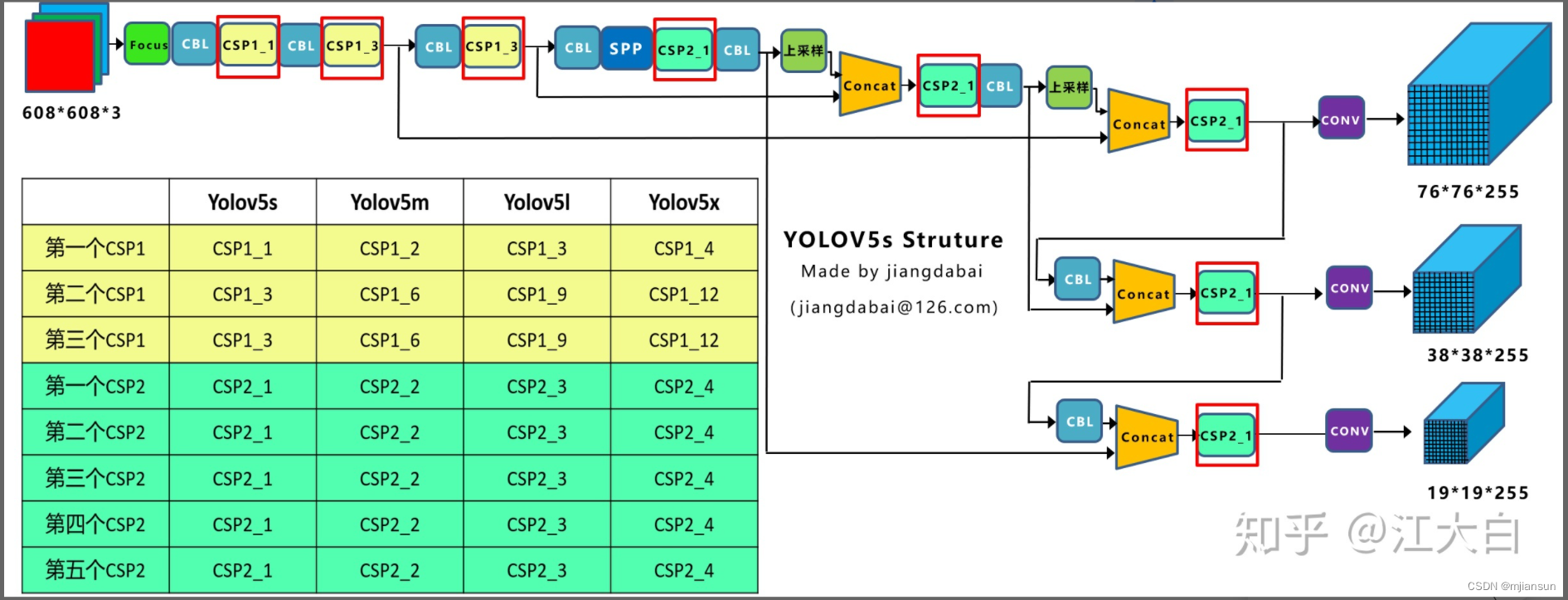
(1)不同网络的深度
在上图中画了两种CSP结构,CSP1和CSP2,其中CSP1结构主要应用于Backbone中,CSP2结构主要应用于Neck中。
需要注意的是,四种网络结构中每个CSP结构的深度都是不同的。
a.以yolov5s为例,第一个CSP1中,使用了1个残差组件,因此是CSP1_1。而在Yolov5m中,则增加了网络的深度,在第一个CSP1中,使用了2个残差组件,因此是CSP1_2。
而Yolov5l中,同样的位置,则使用了3个残差组件,Yolov5x中,使用了4个残差组件。
其余的第二个CSP1和第三个CSP1也是同样的原理。
b.在第二种CSP2结构中也是同样的方式,以第一个CSP2结构为例,Yolov5s组件中使用了2×X=2×1=2个卷积,因为X=1,所以使用了1组卷积,因此是CSP2_1。
而Yolov5m中使用了2组,Yolov5l中使用了3组,Yolov5x中使用了4组。
其他的四个CSP2结构,也是同理。
Yolov5中,网络的不断加深,也在不断增加网络特征提取和特征融合的能力。
(2)控制深度的代码
控制四种网络结构的核心代码是yolo.py中下面的代码,存在两个变量,n和gd。
我们再将n和gd带入计算,看每种网络的变化结果。

(3)验证控制深度的有效性
我们选择最小的yolov5s.yaml和中间的yolov5l.yaml两个网络结构,将gd(depth_multiple)系数带入,看是否正确。

a. yolov5s.yaml
其中depth_multiple=0.33,即gd=0.33,而n则由上面红色框中的信息获得。
以上面网络框图中的第一个CSP1为例,即上面的第一个红色框。n等于第二个数值3。
而gd=0.33,带入(2)中的计算代码,结果n=1。因此第一个CSP1结构内只有1个残差组件,即CSP1_1。
第二个CSP1结构中,n等于第二个数值9,而gd=0.33,带入(2)中计算,结果n=3,因此第二个CSP1结构中有3个残差组件,即CSP1_3。
第三个CSP1结构也是同理,这里不多说。
b. yolov5l.xml
其中depth_multiple=1,即gd=1
和上面的计算方式相同,第一个CSP1结构中,n=3,带入代码中,结果n=3,因此为CSP1_3。
下面第二个CSP1和第三个CSP1结构都是同样的原理。
2.3.4 Yolov5四种网络的宽度
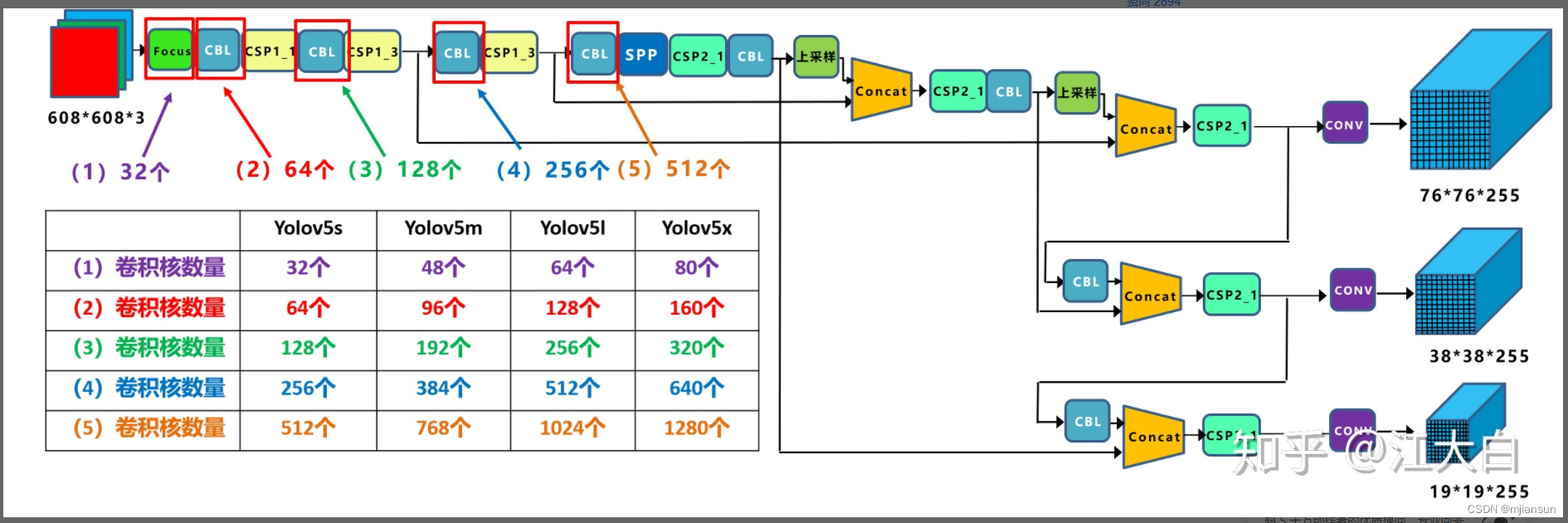
(1)不同网络的宽度:
如上图表格中所示,四种yolov5结构在不同阶段的卷积核的数量都是不一样的,因此也直接影响卷积后特征图的第三维度,即厚度,可表示为网络的宽度。
a.以Yolov5s结构为例,第一个Focus结构中,最后卷积操作时,卷积核的数量是32个,因此经过Focus结构,特征图的大小变成30430432。
而yolov5m的Focus结构中的卷积操作使用了48个卷积核,因此Focus结构后的特征图变成30430448。yolov5l,yolov5x也是同样的原理。
四种不同结构的卷积核的数量不同,这也直接影响网络中,比如CSP1,CSP2等结构,以及各个普通卷积,卷积操作时的卷积核数量也同步在调整,影响整体网络的计算量。
大家最好可以将结构图和前面第一部分四个网络的特征图链接,对应查看,思路会更加清晰。
当然卷积核的数量越多,特征图的厚度,即宽度越宽,网络提取特征的学习能力也越强。
2)控制宽度的代码
在yolov5的代码中,控制宽度的核心代码是yolo.py文件里面的这一行:
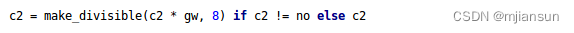
它所调用的子函数make_divisible的功能是:

(3)验证控制宽度的有效性
我们还是选择最小的yolov5s和中间的yolov5l两个网络结构,将width_multiple系数带入,看是否正确。

a. yolov5s.yaml
其中width_multiple=0.5,即gw=0.5。
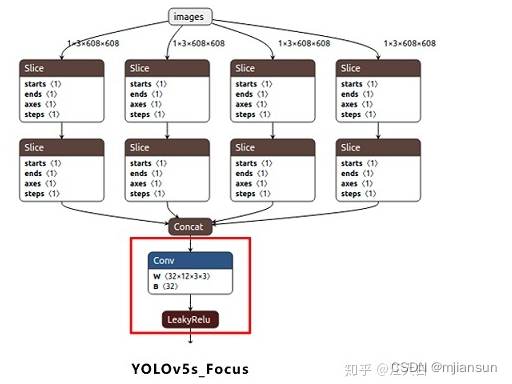
以第一个卷积下采样为例,即Focus结构中下面的卷积操作。
按照上面Backbone的信息,我们知道Focus中,标准的c2=64,而gw=0.5,代入(2)中的计算公式,最后的结果=32。即Yolov5s的Focus结构中,卷积下采样操作的卷积核数量为32个。
再计算后面的第二个卷积下采样操作,标准c2的值=128,gw=0.5,代入(2)中公式,最后的结果=64,也是正确的。
b. yolov5l.yaml
其中width_multiple=1,即gw=1,而标准的c2=64,代入上面(2)的计算公式中,可以得到Yolov5l的Focus结构中,卷积下采样操作的卷积核的数量为64个,而第二个卷积下采样的卷积核数量是128个。
另外的三个卷积下采样操作,以及yolov5m,yolov5x结构也是同样的计算方式,大白这里不过多解释。