数据集简单介绍

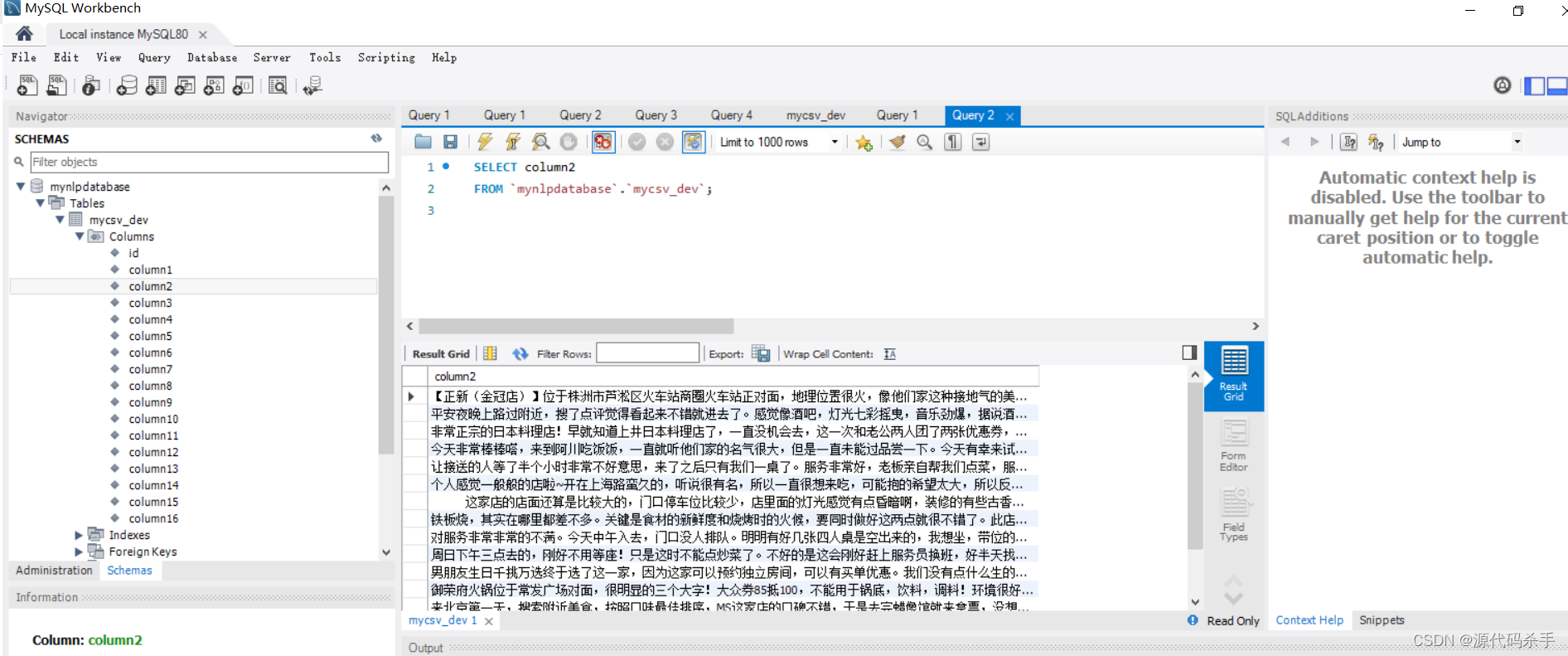
美团点评数据集 (Meituan-Dianping/asap) 是一个中文自然语言处理 (NLP) 数据集，由美团点评公司收集和发布。该数据集用于评估和开发中文文本分类和情感分析模型，包括情感极性分类、食物安全文本分类和自定义分类等任务。

数据集包含两个部分：训练集和测试集。训练集共包含20万条评论，其中13.5万条正向评论和6.5万条负向评论。测试集包含5万条评论，其中3.5万条正向评论和1.5万条负向评论。所有的评论都来自美团点评网站上的真实用户，包括用户对餐厅、美食、酒店、旅游景点、电影等的评论。

该数据集的标注方式为情感极性分类，分为正向和负向两个类别。数据集的分布均匀，类别之间的比例为正向评论与负向评论的比例为 2:1。每个样本的标签是人工标注的，该数据集的标注精度很高。

此外，该数据集还提供了一些其他的信息，如评论内容、所属分类、商户名称、评论时间等。

Meituan-Dianping/asap 数据集已被广泛用于中文情感分析、文本分类等任务的研究和评测。通过使用该数据集进行实验和比较，研究人员可以更好地评估和改进其模型的性能。

该数据集可以通过美团点评官方网站或者 GitHub 上进行下载和使用。

数据集参考地址：