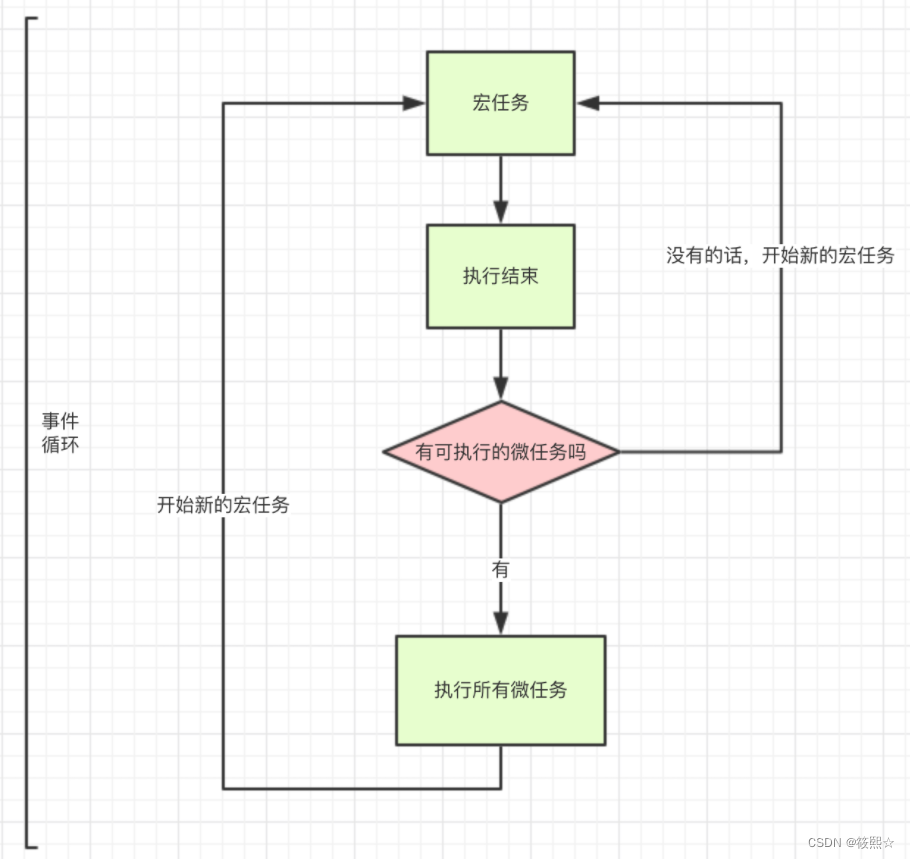
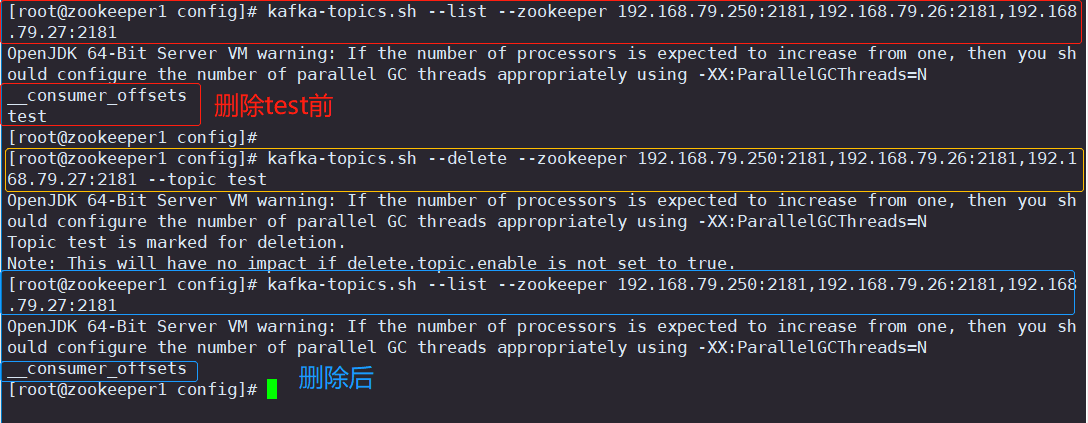
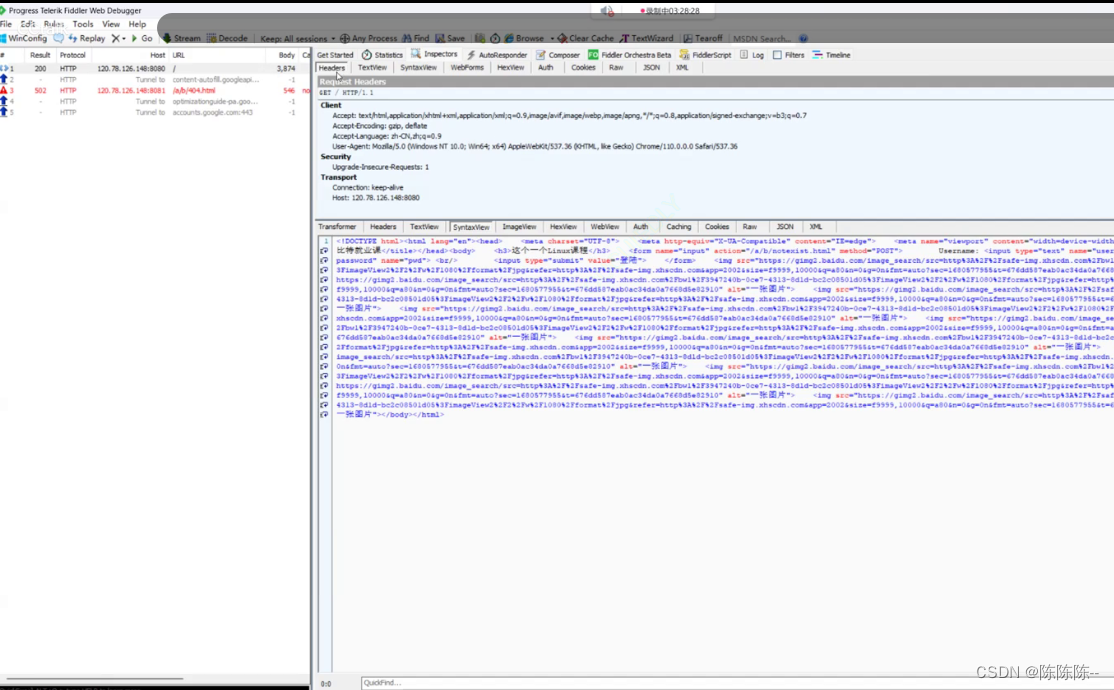
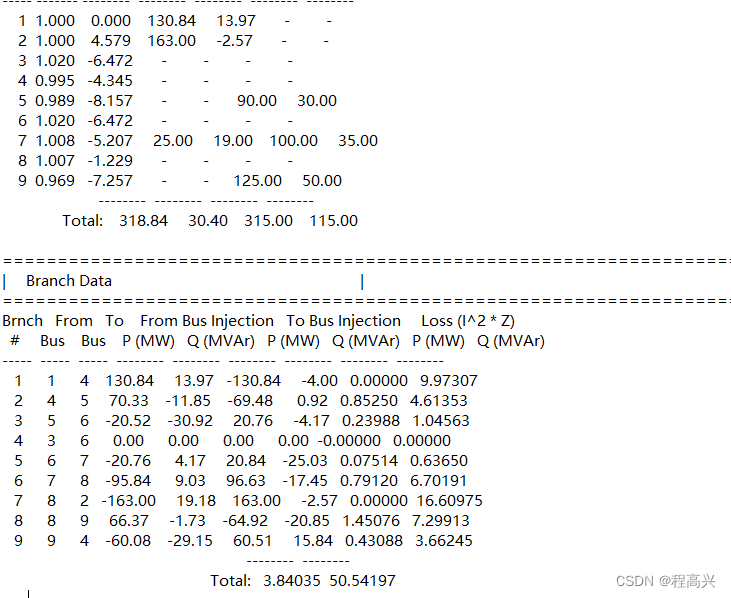
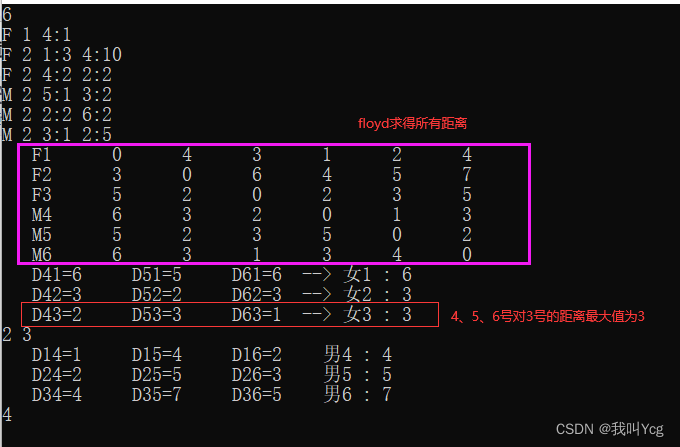
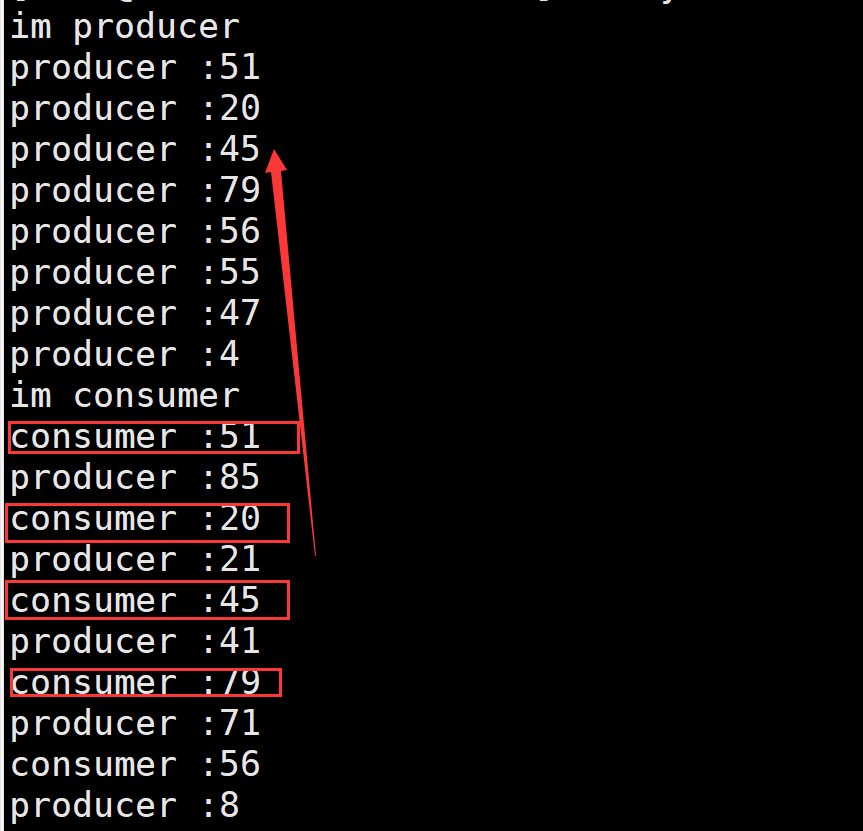
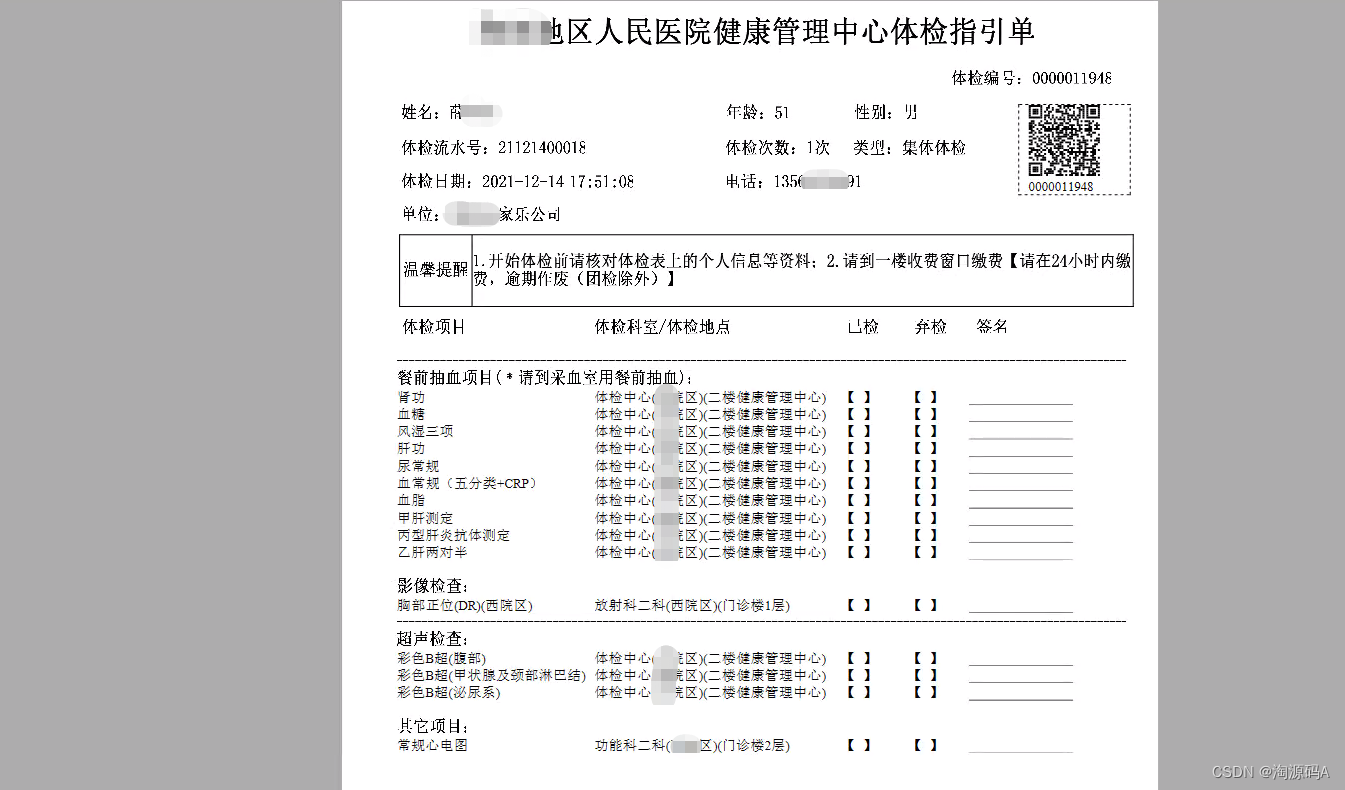
高斯消元法流程

首先必须要判断矩阵是不是一个方阵，其方法是对于一个矩阵$A_{n\times n}$，先构造一个增广矩阵$W=[A\mid E]$，其中$E$是一个$n\times n$的单位矩阵，这样$W$就成了一个$n\times 2n$的矩阵。接下来对$W$进行行变换，使之变成的形式$[E\mid B]$，这样就可以确定$A^{-1}=B$。

举个例子，以下矩阵：

$\left[\begin{array}{cccc}1& 1& 1& 1\\ 2& 1& 1& 1\\ -1& 2& 1& 1\\ -3& 2& 1& 2\end{array}\right]$

右接一个单位矩阵：

$\left[\begin{array}{cccccccc}1& 1& 1& 1& 1& 0& 0& 0\\ 2& 1& 1& 1& 0& 1& 0& 0\\ -1& 2& 1& 1& 0& 0& 1& 0\\ -3& 2& 1& 2& 0& 0& 0& 1\end{array}\right]$

进行行变换，得到行阶梯矩阵：

$\left[\begin{array}{cccccccc}1& 1& 1& 1& 1& 0& 0& 0\\ 0& 1& 1& 1& 2& -1& 0& 0\\ 0& 0& -1& -1& -5& 3& 1& 0\\ 0& 0& 0& 1& -2& 2& -1& 1\end{array}\right]$

进行单位化：

$\left[\begin{array}{cccccccc}1& 0& 0& 0& -1& 1& 0& 0\\ 0& 1& 0& 0& -3& 2& 1& 0\\ 0& 0& 1& 0& 7& -5& 0& -1\\ 0& 0& 0& 1& -2& 2& -1& 1\end{array}\right]$

利用高斯消元法求矩阵的逆如Algorithm1。

由Algorithm1看出，利用高斯消元法求矩阵的逆的时间复杂度是$2\times O\left(n^3\right)$。在$n$越大的情况下，该方法消耗的计算成本远远小于伴随矩阵法。

高斯消元法代码实现

function B = gaussianElimination(A)
%用高斯消元法(伴随矩阵法)求矩阵的逆
%   A:原矩阵
%   B:逆矩阵
n = size(A,1);  %方阵的维度
B = eye(n);  %初始化B矩阵为单位矩阵
for i0 = 1 : n
    pe = max(abs(A(i0 : n, i0)));   %寻找主元pe,max目的是通过主元判断矩阵是否可逆
    if pe == 0      %判断主元是否为0, 若是, 则矩阵A不是满秩矩阵,不存在逆矩阵
        disp("该矩阵A不存在逆矩阵")
        return;
    end
    %消去A的第i0列除去i0行以外的各行元素
    tmp1 = A(i0, i0);
    A(i0, :) = A(i0, :) / tmp1;   %主对角线上的元素变为1
    B(i0, :) = B(i0, :) / tmp1;   %伴随矩阵做相应变换
    for i1 = 1 : n
        if i1 ~= i0
            temp = A(i1, i0);
            A(i1, :) = A(i1, :) - A(i0, :) .* temp;
            B(i1, :) = B(i1, :) - B(i0, :) .* temp;
        end
    end
end
end

clc;close;clear;
X = [8, 4, 5; 4, 8, 6; 5, 6, 8];
tic
B = gaussianElimination(X);
toc
tic
c = inv(X);
toc
disp(B);
disp(c);

输出结果：