前言：我们在求解逆序对问题时题目往往会给我们加大数据量，防止我们以暴力的方式通过该题，所以在遇到有关求解逆序对问题的时候，我们有必要知道一些具体的优化方法，对于逆序对我们，我们一般的会有两种标准求解方法：归并排序和树状数组，接下来我就分别来介绍这两种方法的原理和实现，争取能让你们一文精通逆序对问题。

话不多说，正文开始：

目录

1.背景引入：

2.归并排序思路

3.树状数组法（注意数组要从下标1开始用）

3.1树状数组和前缀和

3.1.2 lowbit函数

树状数组求解前缀和

3.2树状数组求解逆序对个数

4.金句省身

---

1.背景引入：

 

 这是一道简单的逆序对计数问题，我们需要找到所有的逆序对的数目并返回。

2.归并排序思路

     我们都知道，我们在学习归并排序时是将划分成的每个小子区间内的逆序的两个元素进行交换，然后将这个小子区间的排好序的元素按原位置，这点很重要，这里我以图的形式来表述，希望可以更好的帮助理解：

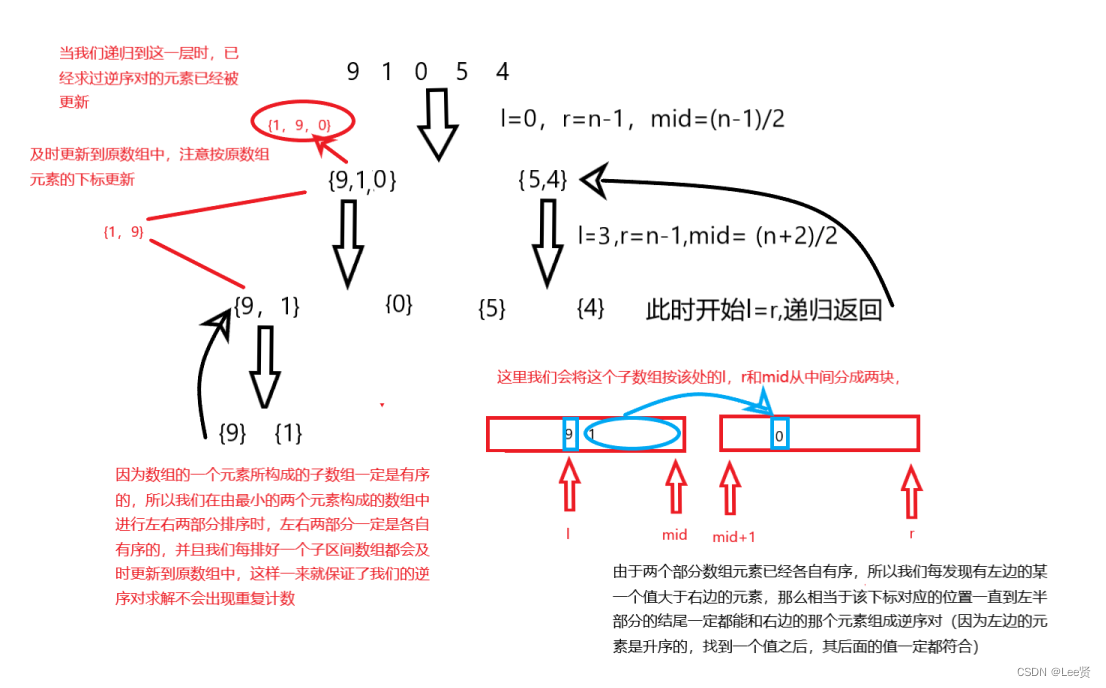
不知道好不好理解，但是按我的理解只能画成这样了，下面我们再根据上面的思想写代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn = 5e5 + 5;
typedef long long ll;
ll mem[maxn];
ll temp[maxn];
ll n;
ll ans = 0;
void memerg(ll l, ll r)
{
	if (l >= r)
		return; //递归返回条件
	ll mid = (l + r) >> 1;
	memerg(l, mid);
	memerg(mid + 1, r);
	ll i = l, j = mid + 1, t = 0;
	while (i <= mid && j <= r)
	{
		if (mem[i] > mem[j])
		{
			temp[t++] = mem[j++];
			ans += mid - i + 1;//左半部分的i-mid都可以和j组成逆序对
		}
		else
		{
			temp[t++] = mem[i++];
		}
	}
	while (i <= mid) temp[t++] = mem[i++];
	while (j <= r)temp[t++] = mem[j++];
	for (ll k = 0; k < t; k++)
		mem[l + k] = temp[k];//注意这个地方是个易错点，一定要按照原数组对应的下标返回排好序的值，这样才会保证逆序对不会出现重复解

}
int main()
{
	while (scanf("%d", &n) && n != 0)
	{
		memset(mem, 0, sizeof(mem));
		for (ll i = 0; i < n; i++)
			scanf("%lld", &mem[i]);
		ans = 0;
		memerg(0, n - 1);
		printf("%lld\n", ans);
	}
	return 0;
}

3.树状数组法（注意数组要从下标1开始用）

3.1树状数组和前缀和

树状数组是利用数的二进制特征进行检索的一种树状的结构，所以首先，我们要先来了解一下，树状数组的原理和其求前缀和所带来的高效性：

假设我们对一个长度高达几百万的数组求前缀和，我们需要怎么优化呢？这里我们可以应用线段树的思想：

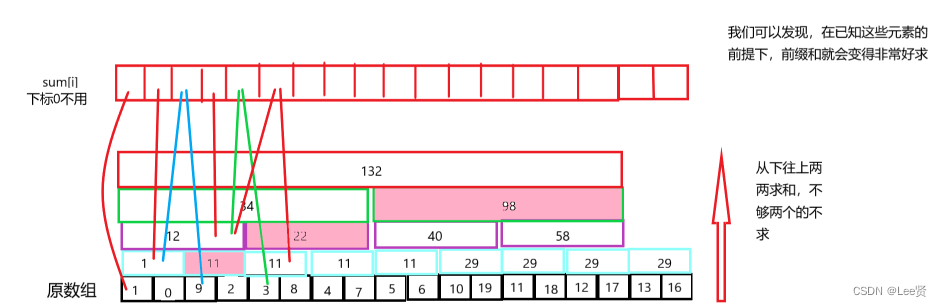
 接着，我们会发现，每一行的第偶数个元素在求前缀和时都会有更好的方法，所以这个数据我们是用不到的，于是我们将其从图中删除，就变成这样：（请忽略这些蓝线）

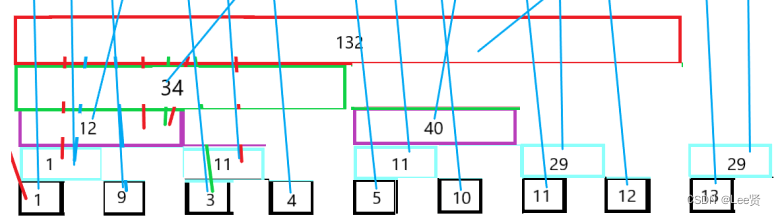
 到这里学过数据结构的就有点坐不住了，这......我咋看咋那么像个二叉树呢？于是，我们就将它按二叉树的形式展开（顺便对其进行中序遍历）：

 接着，我们在引入树状数组的核心：lowbit函数

3.1.2 lowbit函数

int lowbit(int x)
{
    return x & (-x);//涉及负数的补码和正数补码的计算，这里不在展开
}

功能：找到一个数二进制数中的最后一个1，并返回这个1所代表的权值，其原理是利用了负数的补码表示

我们将我们前面求出的结构再次给出：

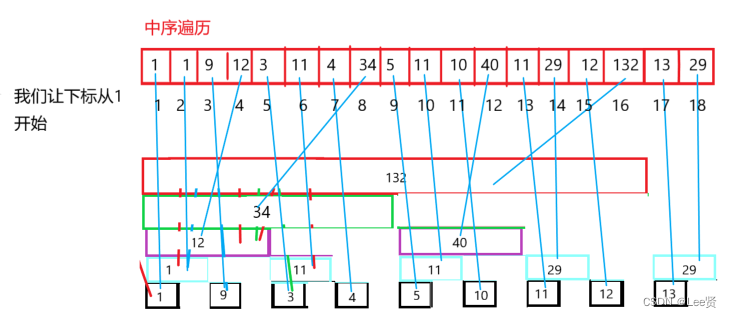
我们不难发现如下规律：

对于每一行元素，他们的lowbit值都是一样的：

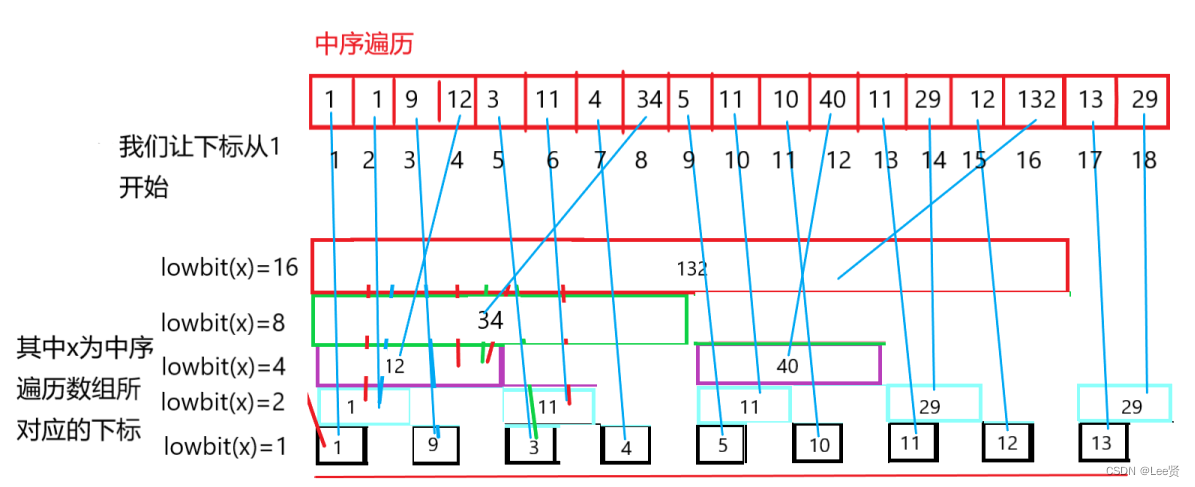
 那么，这对我们求解前缀和的算法优化有什么帮助呢？我们现在来分析

树状数组求解前缀和

我们可以发现，中序遍历数组中的下标和lowbit可以产生联系，这里来举个例子：

       假设中序遍历数组为tree，我们以tree[6]=11为例，我们知道，6的二进制位110，6=4+2，我们从图中看出tree[6]的这个11并不是前6项的和，这个11其实是第六项和第五项的和，怎么办，我们还差前四项的和，而我们的前四项的和储存在tree[4]中，也就是说，我们的sum[6]=tree[6]+tree[4]，我们再和前面的lowbit函数结合一下，我们就可以得到求解前缀和的一般形式：

int lowbit(int x)
{
	return x & (-x);//涉及负数的补码和正数补码的计算，这里不在展开
}
int sum(int x)
{
	int ans = 0;
	while (x)
	{
		ans += tree[x];
		x -= lowbit(x);  //比如sum[6]=tree[2]+tree[4](6的二进制位110)
	}
	return ans;
}

这里为了证明求解是对的，我给出这个数组的求解和标椎前缀和对比，

int tree[20] = { 0,1,1,9,12,3,11,4,34,5,11,10,40,11,29,12,132,13,29 };
int lowbit(int x)
{
	return x & (-x);//涉及负数的补码和正数补码的计算，这里不在展开
}
int s(int x)
{
	int ans = 0;
	while (x)
	{
		ans += tree[x];
		x -= lowbit(x);
	}
	return ans;
}
int main()
{
	int arr[19] = { 0,1,0,9,2,3,8,4,7,5,6,10,19,11,18,12,17,13,16 };
	int sum[20]={0};
	for (int i = 1; i <= 18; i++)
	{
		sum[i] = sum[i - 1] + arr[i];
		printf("%d  %d\n", sum[i],s(i));
	}
	return 0;
}

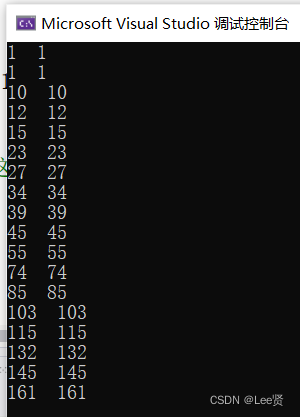
这样一来，我们求解数据量大的数组的前缀和的时候，就可以只进行十几次加法就可以实现，大大提高了时间效率。

我们前面是给出了一个新的tree数组来代替原数组进行前缀和的求解，下面我们需要给出tree数组的实现方式：

我们可以列出几组值：

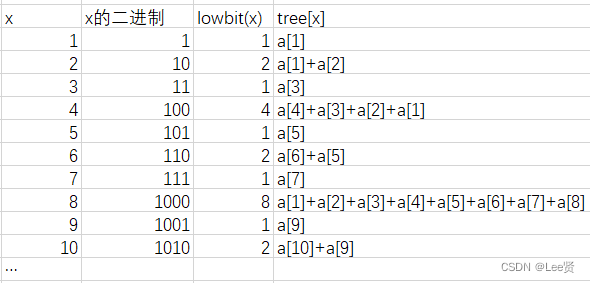
我们和树状数组来做比对：

 其中红色部分的数字表示树状数组的下标，这样我们的的树状数组就相对清晰了

 我们发现，tree数组的元素个数和  lowbit（x）竟然相等，换句话说，tree[x]的值是把a[x]和它前面的共lowbit(x)个数相加的结果，那这样我们通过原数组构造出tree数组就相很容易了，这里实现就不再给出，但是我们这里给出一种更加简便的实现方法：

tree[x]能够以二分的复杂度存储一个数列的数据，具体的，tree[x]中存储的是原数组区间

[x-lowbit(x)+1,x]中的每个数的和，

 单点值修改对tree的影响

如果说我们需要修改原数组中某个下标处的值，对于我们的tree数组来说，只需要改变由其算出的tree的部分的值即可，

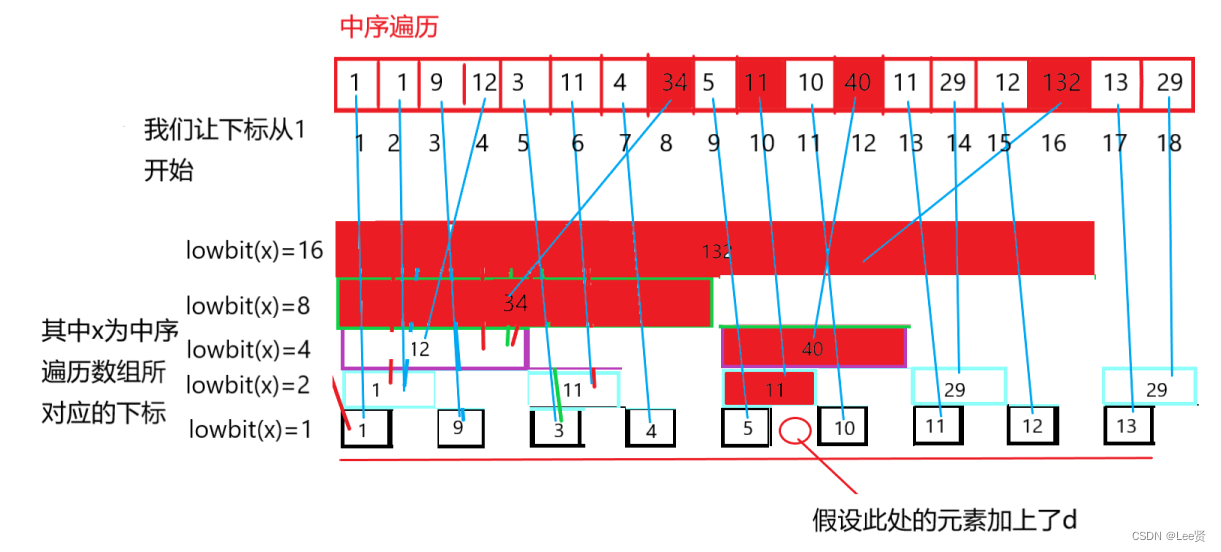
 这里注意我们修改的值可能在原始下标的左边或者右边，我们需要判断:

int updata(int x, int d)
{
	int temp = x;
	while (temp > 0)
	{
		tree[temp] += d;
		temp -= lowbit(temp);
	}
	while (x <= N)
	{
		tree[x] += d;
		x += lowbit(x);
	}

}

3.2树状数组求解逆序对个数

前面我们说了那么多，为逆序对的求解做了理论基础，现在，我们正式的来看逆序对问题，逆序对问题的关键就是将原数组中的数字看做树状数组的下标，，比如我们的序列是{5,4,2,6,3,1}，那么对应的我们的树状数组就是tree[5],tree[4],tree[2],tree[6],tree[3],tree[1]。

首先，什么是离散化？我们为什么要用到离散化？

第一，离散化是在数据差异较大的情况下并且只有数据间的相对大小比较重要时，我们就需要把这些差异较大的数变成相邻的，但是仍能表示相对大小关系的数，离散化（Discretization），把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。

接着，对于我们的逆序对的求法，我们有倒序和逆序的两种方法，这两种方法都有一个共同的原理，就是当前待加入的元素与前面已经加入的元素所构成的逆序对关系

倒序：

数字1，把tree[1]加1，因为我们将1加入到了树状数组的相对应的位置，所以我们就可以数一数在加入1之后其前面的的元素有几个，也就是sum（0）的个数，sum（0）中每一个元素都能与1做成逆序对，同理，我们求解其他元素也是如此；

正序：

对于数字5，我们把5加入树状数组，即tree[5]++,那么我们可以用当前已经加入元素的个数减去sum（5），注意，我们的数字5加入也算在内，因为我们算的是逆序对，所以只要是大于5的元素，在5加入之前加入，那么其就会和5组成一个逆序对。

下面是我们的代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e5 + 1;
typedef long long ll;
ll tree[maxn],temp[maxn];
ll n;
ll ans = 0;
struct node {
	ll val, order;
	bool operator<(const node& b)
	{
		if (this->val == b.val)
			return this->order < b.order;//如果有元素相等，那么返回先读到的那一个
		return this->val < b.val;
	}
}a[maxn];//设为结构体是为了方便我们排序离散化
int lowbit(int x)
{
	return x & (-x);
}
int sum(int x)//求前缀和
{
	int ans = 0;
	while (x > 0)
	{
		ans += tree[x];
		x -= lowbit(x);
	}
	return ans;
}

void updata(int x, int v)//更新树状数组的值
{
	while (x <= n)
	{
		tree[x] += v;
		x += lowbit(x);
	}
}

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &a[i].val);
		a[i].order = i;
	}
	sort(a + 1, a + n+1);//重载运算符实现，也可以用外部比较函数实现
	for (int i = 1; i <= n; i++)
		temp[a[i].order] = i;//离散化

	//正序
	for (int i = 1; i <= n; i++)
	{
		updata(temp[i], 1);
		ans += (i - sum(temp[i]));
	}

	//逆序
	/*for (int i = n; i >= 1; i--)
	{
		updata(temp[i], 1);
		ans += sum(temp[i] - 1);
	}*/
	printf("%lld\n", ans);

	return 0;
}

4.金句省身

        人生越是不顺的时候，就越要沉住气！认清形势，放弃幻想。少点以为，多点作为。你若盛开，蝴蝶自来；你若精彩，天自安排。

      不管命运如何对待你，一定要好好生活，努力提升自己，努力赚钱。等你熬过所有的苦，就会尝到所有的甜。道的规律就是先苦后甜，否极泰来。