矩阵分解报告

1. 试验介绍

矩阵分解就是把原来的大矩阵，近似的分解成小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵。具体来说就是，假设用户物品的评分矩阵R是m乘n维，即一共有m个用户，n个物品。通过一套算法转化为两个矩阵P和Q,矩阵P的维度是m乘k，矩阵Q的维度是n乘k。上述内容即： 。

如下表所示，本试验采用5*4数据表格，每一行代表用户，每一列代表用户对该商品的评分（满分10分），其中“-”表示该用户没有对该商品进行评分。

	Commodity-1	Commodity-2	Commodity-3	Commodity-4
User-1	-	10	5	7
User-2	6	2	6	4
User-3	-	7	9	10
User-4	4	5	-	8
User-5	9	-	5	4

再次使用大型电影评分矩阵数据集进行验证。

2. 算法介绍

2.1损失函数

损失函数使用原始评分矩阵R和重构评分矩阵R之间的误差的平方作为损失函数为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束，即：

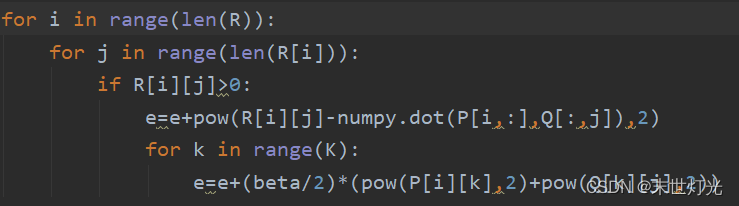
eij2=Rij-Rij2+β2k=1K(P2+Q2)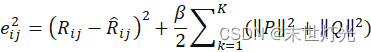

最终，需要求解所有的非“-”项的损失之和的最小值：

minloss=Rij≠-eij2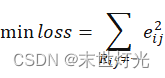

对应关键代码：

2.2使用梯度下降法获得修正的p和q分量

求解损失函数的负梯度：

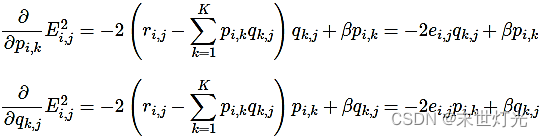
 根据负梯度的方向更新变量：

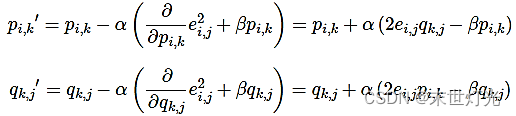
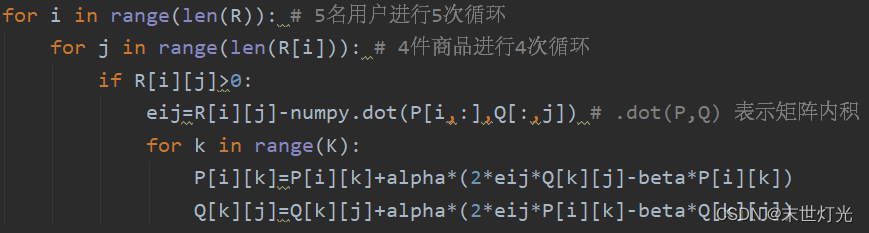
对应关键代码：

3. 实验结果

如图1所示，经过5000步的训练loss呈现下降趋势，在500步左右已经开始收敛。如图2所示，R矩阵通过矩阵分解生成P矩阵和Q矩阵，根据生成的P矩阵和Q矩阵重新生成评价矩阵R_MF。

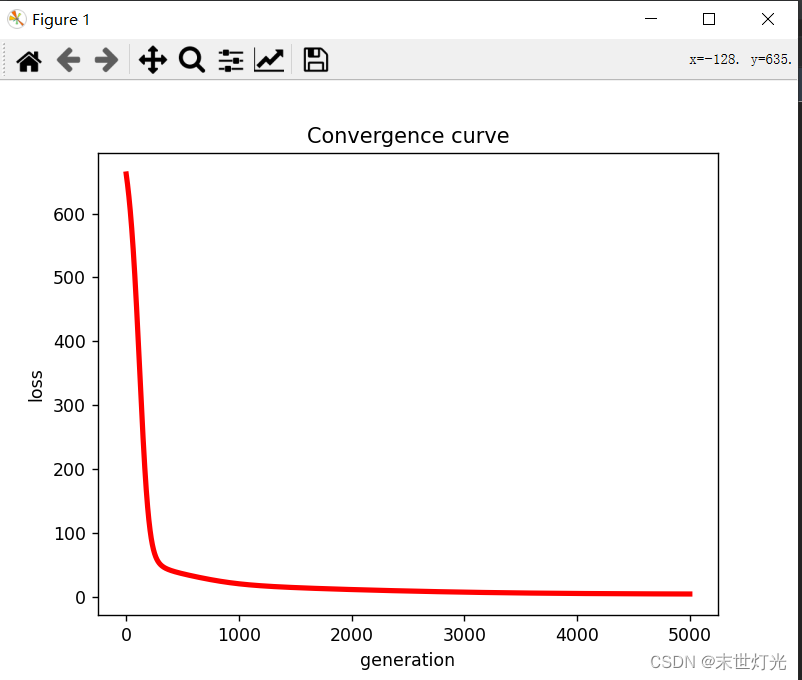
图1 损失曲线

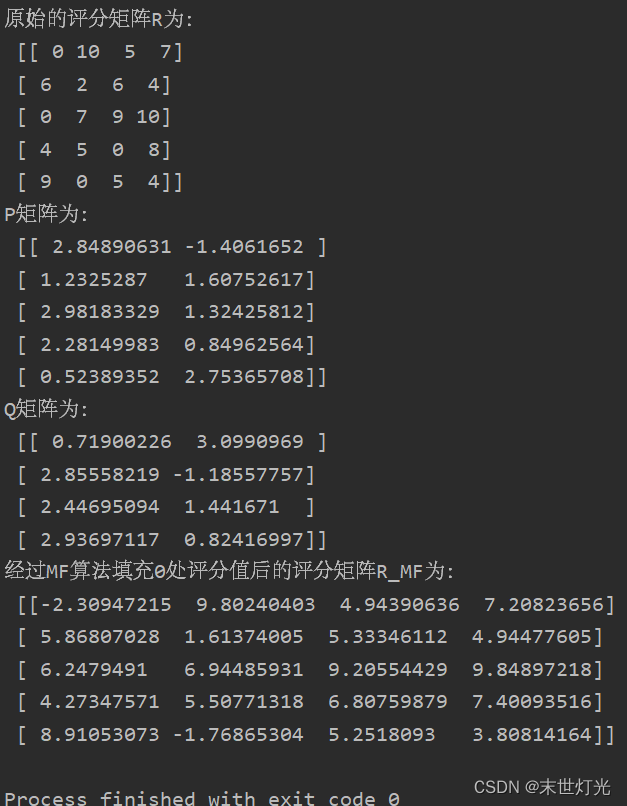
图2 运行结果

电影评分数据集：

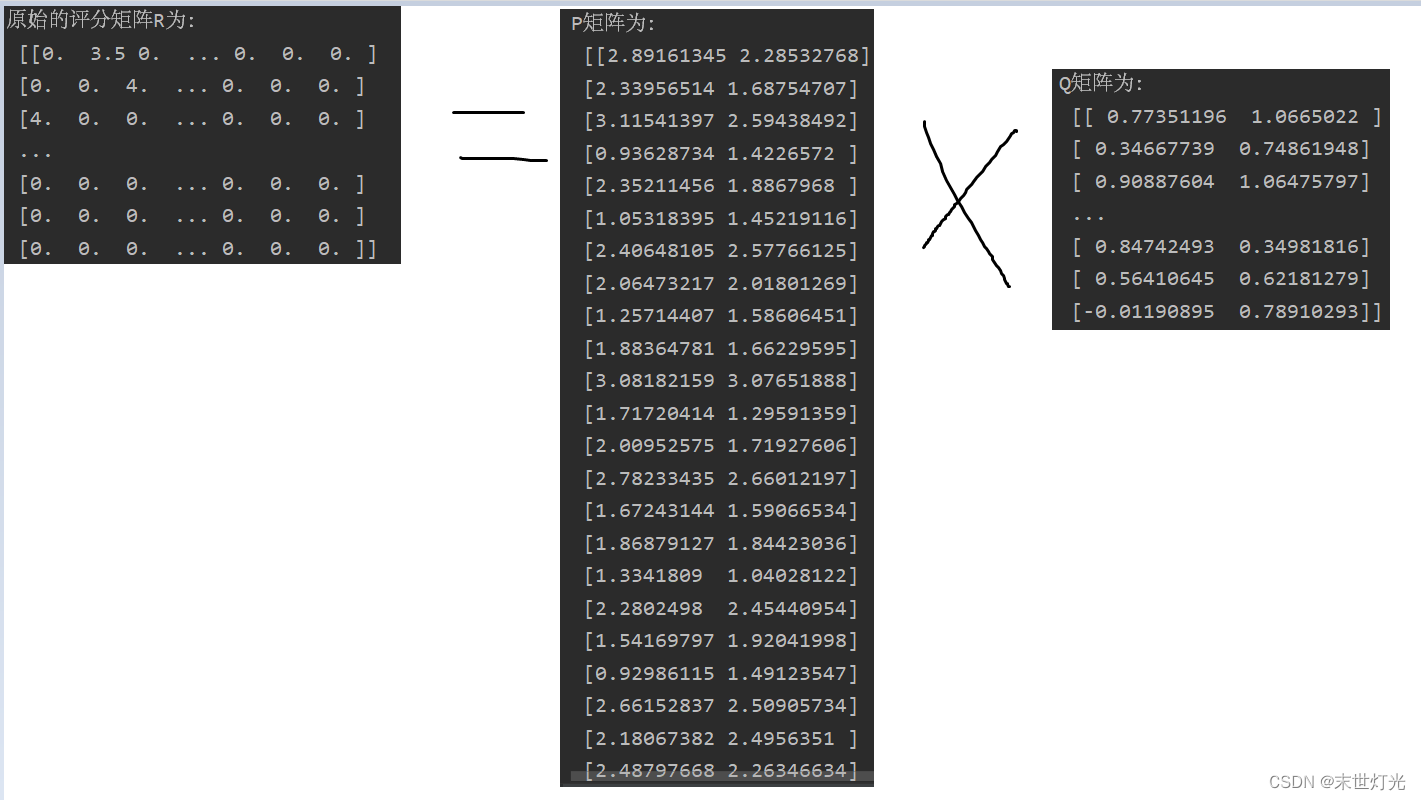
具体资料请前往百度网盘自取：

链接：https://pan.baidu.com/s/1coFpKs_fJVUbrTQUQpq1cg 
提取码：bjx2 
--来自百度网盘超级会员V5的分享