💥 💥 💞 💞 欢迎来到本博客 ❤️ ❤️ 💥 💥
🏆 博主优势: 🌞 🌞 🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳ 座右铭:行百里者,半于九十。
📋 📋 📋 本文目录如下: 🎁 🎁 🎁
目录
💥1 概述
1.1 K-means聚类算法及存在的问题
1.2 ISODATA 聚类算法及存在的问题
1.3 L-ISODATA聚类算法
1.4 K-L-ISODATA聚类算法
📚2 运行结果
2.1 聚类算法比较
2.2 K-L-ISODATA聚类算法
2.3 L-ISODATA聚类算法
2.4 ISODATA聚类算法
2.5 K-means聚类算法
🎉3 参考文献
🌈4 Matlab代码、数据、文章讲解
💥1 概述
文章来源:

对用户进行分类,将每一类用户的负荷叠加,为每个类建立预测模型,如图3.3所示:


先采用聚类算法依据用电行为和习惯对用户进行划分,将具有相似用电习惯的用户分为同一类,同一类的用户的用电数据叠加在一起,再为每一类建立负荷预测模型。这种做法综合了上述两种策略,取长补短,既可以避免为每个用户都建立预测模型带来的问题,同时又可以加强对不同用电特性的用户的学习能力,提高预测准确性。如上述分析,为了提高预测模型对用户的用电模式这一特征的表示能力,同时避免为每个用户都建立预测模型,本文采用第三种策略来进行负荷预测,需要根据用户的用电习惯将用户进行分类。用户的用电行为和习惯可以从其历史负荷曲线中分析得到,
具有相似的用电行为和习惯的用户,它们的历史负荷曲线也会是相似的[46]。因此可以从历史负荷曲线入手,使用聚类算法来对用户的历史负荷曲线进行划分,采用距离度量来评价负荷曲线间的相似性,将具有相似负荷曲线的用户划分到同一类中,负荷曲线不的用户划分为不同的类。对负荷曲线聚类后,可以针对每一类用户的用电行为单独迂进行分析,建立更加精准的负荷预测模型。在进行负荷曲线聚类之前,首先要对负荷曲线进分析,建立更加精准的负荷预测模型。在进行负荷曲线聚类之前,首先要对负荷曲线进行归一化处理,这是因为不同的用户其负荷的量级可能有较大差距,而负荷曲线聚类主要是评估用户的用电行为和习惯,也就是负荷曲线的走向和趋势,与负荷的数量级是无关的,因此事先对负荷曲线进行归一化处理是非常重要的。根据第二章的分析,可以采
用线性函数归一化来处理负荷曲线。
1.1 K-means聚类算法及存在的问题
K-means聚类算法在1967年被James MacQueen提出,是一种数据挖掘中非常常用的聚类算法I:8]。K-means聚类算法会将样本集划分为k类,每一类都有一个聚类中每个样本离哪个聚类中心最近就被划分为哪一类。K-means通过迭代来进行簇的划分,最终的目标是使得簇内的误差最小化。


K-means同时还具有一些缺点:
(1)k值的选取不容易提前确定,尤其是在样本集数据量大、维度高时,设定的k值得到的结果也是不一样的;
(2)初始的聚类中心是随机选取的,如果选取的不合适会导致收敛速度变慢,并且可能影响聚类的效果;
(3)对噪声和异常点比较敏感;
(4)不适合太离散、样本类别不平衡的聚类任务;
(5)距离度量的选取对聚类效果非常关键。
1.2 ISODATA 聚类算法及存在的问题
ISODATA 的全称是迭代自组织数据分析算法(Iterative Selforganizing Data Ana.lysisTechniques Algorithm),在K-means中,k的值需要人为提前确定,并且k的值一旦确定也就无法修改,在很多场景,尤其是数据量大、数据维度多的场景中,k的值很难提前就确定下来,往往只能多次尝试找到最优的k值。ISODATA聚类算法的出现解决了这样一个问题,它的k值是在聚类过程中可以变
动的,它主要引入了分裂和合并这两个操作:当某个类别中样本数很多并且方差较大时,则分裂该类别为两个类;当某个类别中样本数过少时并且离另一个类别靠的比较近,则对这两个类进行合并操作[49]。
综上所述,ISODATA算法和K-means算法的最大不同是新增了合并和分裂这两个操作,也因此引入了很多参数。ISODATA算法也有一定的优缺点,ISODATA最大的优点在于:ISODATA算法虽然也需要预先给出一个期望得到的聚类数目,但在运行期间ISODATA算法会根据各个聚类的实际情况而动态调整聚类数目,可以有效地解决事先无法确定聚类数目的问题。
然而,虽然ISODATA算法解决了K-means 的一些问题,但它仍旧有自己的缺点和局限性:
(1)首先,ISODATA依旧是随机选取初始聚类中心,选取的结果会影响到聚类收敛的速度和最终聚类的效果;
(2)ISODATA默认和K-means一样都使用欧式距离作为距离度量,在原始的负荷曲线输入空间中使用欧氏距离无法提取负荷曲线中的高维特征,这在前面已经分析过了;
(3 )ISODATA 算法需要预先确定的参数更多,算法的复杂度更高,比如标准偏差参数、聚类中心最小距离参数,这些参数都需要事先根据一些统计量来进行估计。
1.3 L-ISODATA聚类算法
经典的ISODATA 聚类算法虽然已经解决了K-means算法需要事先确定聚类数目的问题,但它还是有一定的缺点:比如随机选取初始聚类中心可能导致聚类算法收敛较慢、效果较差,还会造成聚类结果的偶然性;以及原始的负荷曲线输入空间中选取欧式距离作为距离度量无法捕捉到负荷曲线中的高维特征。本文提出 L-ISODATA 聚类算法,即Load curve-ISODATA 算法,将ISODATA算法应用在负荷曲线聚类领域中,并对ISODATA聚类算法进行改进。
1.4 K-L-ISODATA聚类算法
📚2 运行结果
2.1 聚类算法比较
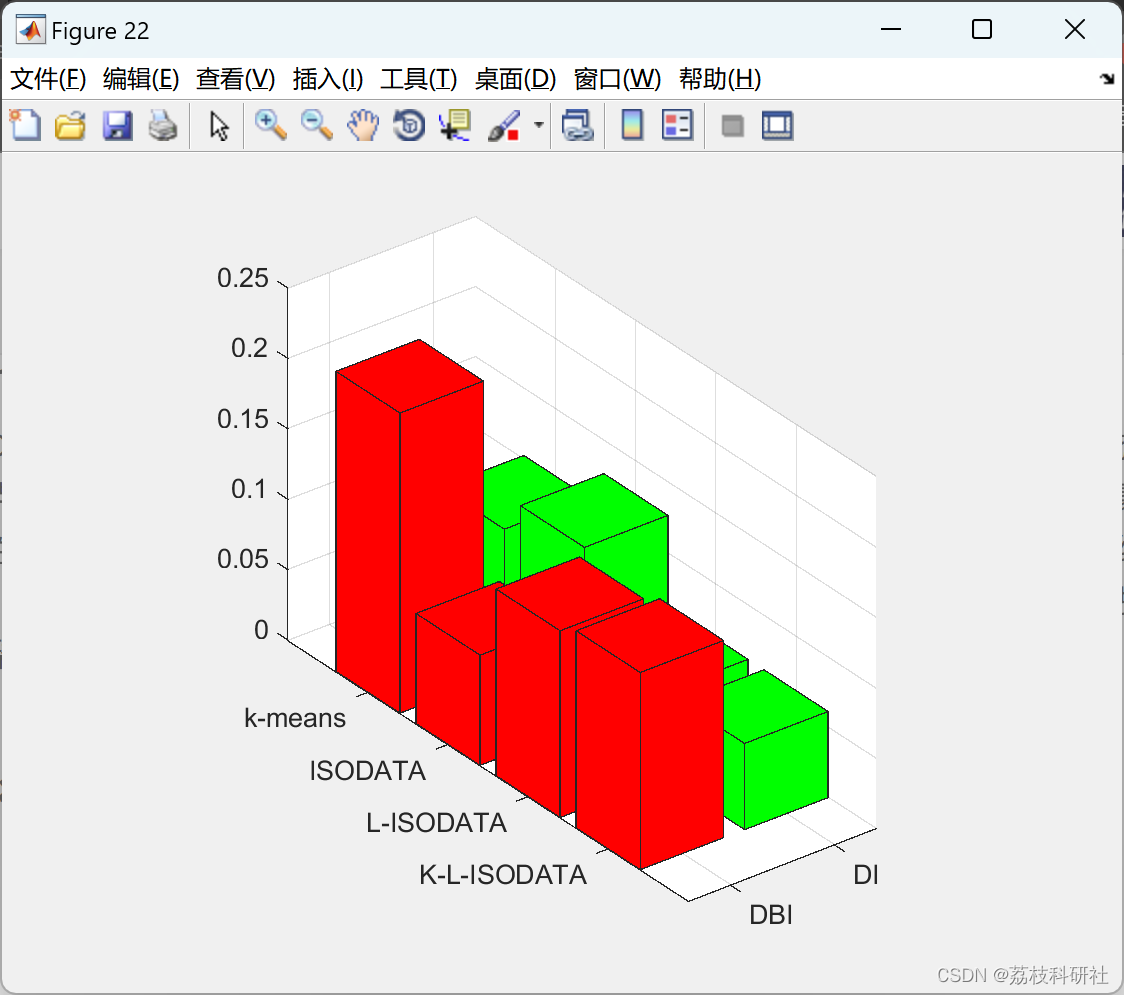

2.2 K-L-ISODATA聚类算法
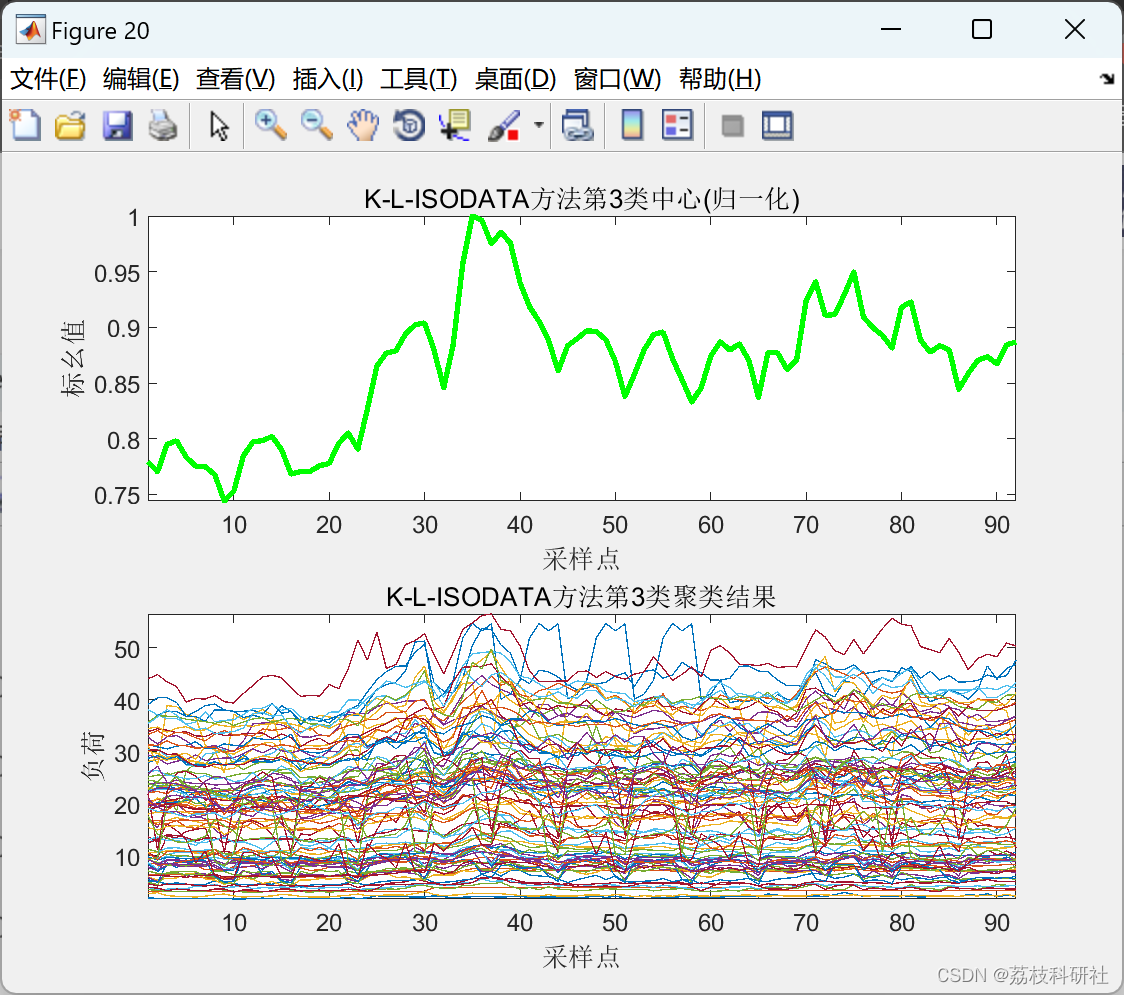

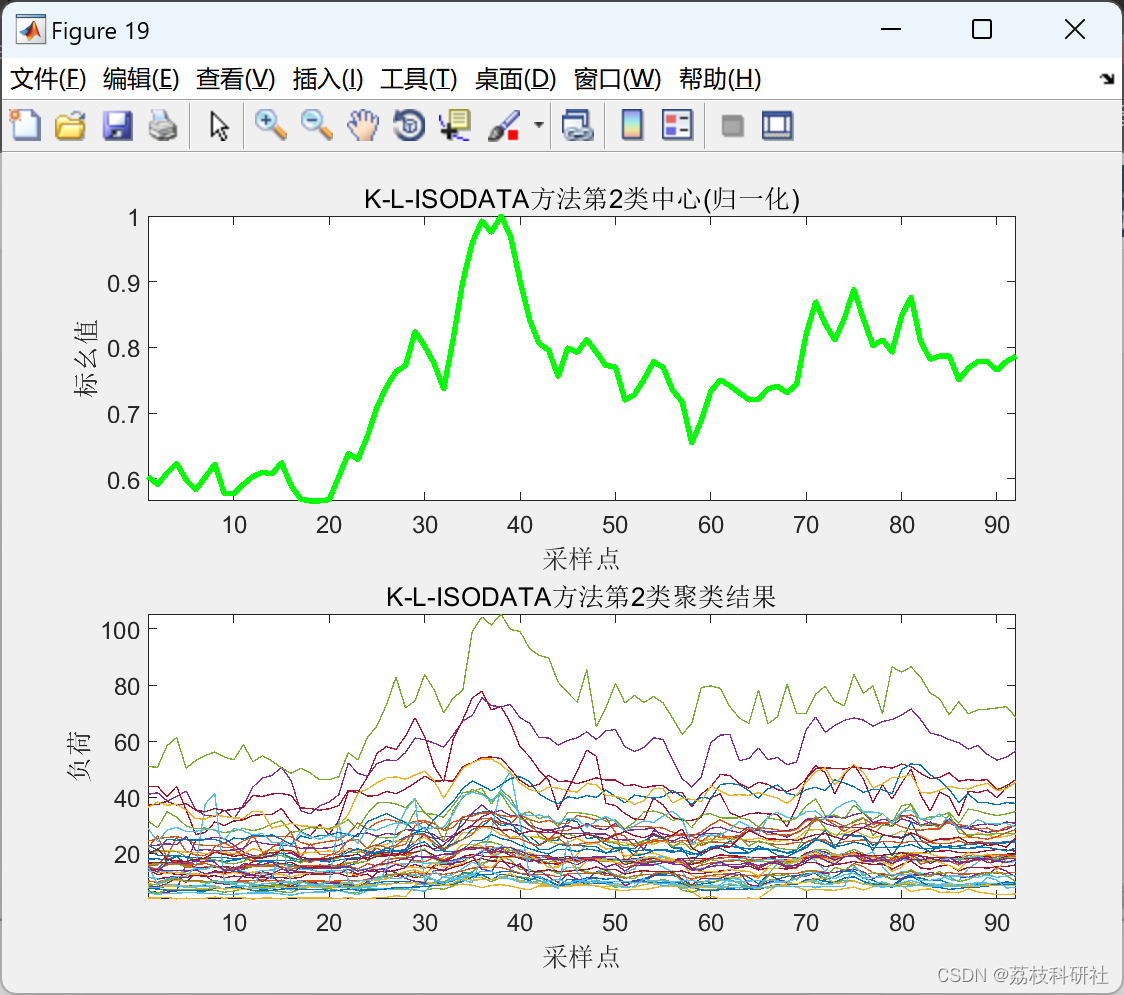

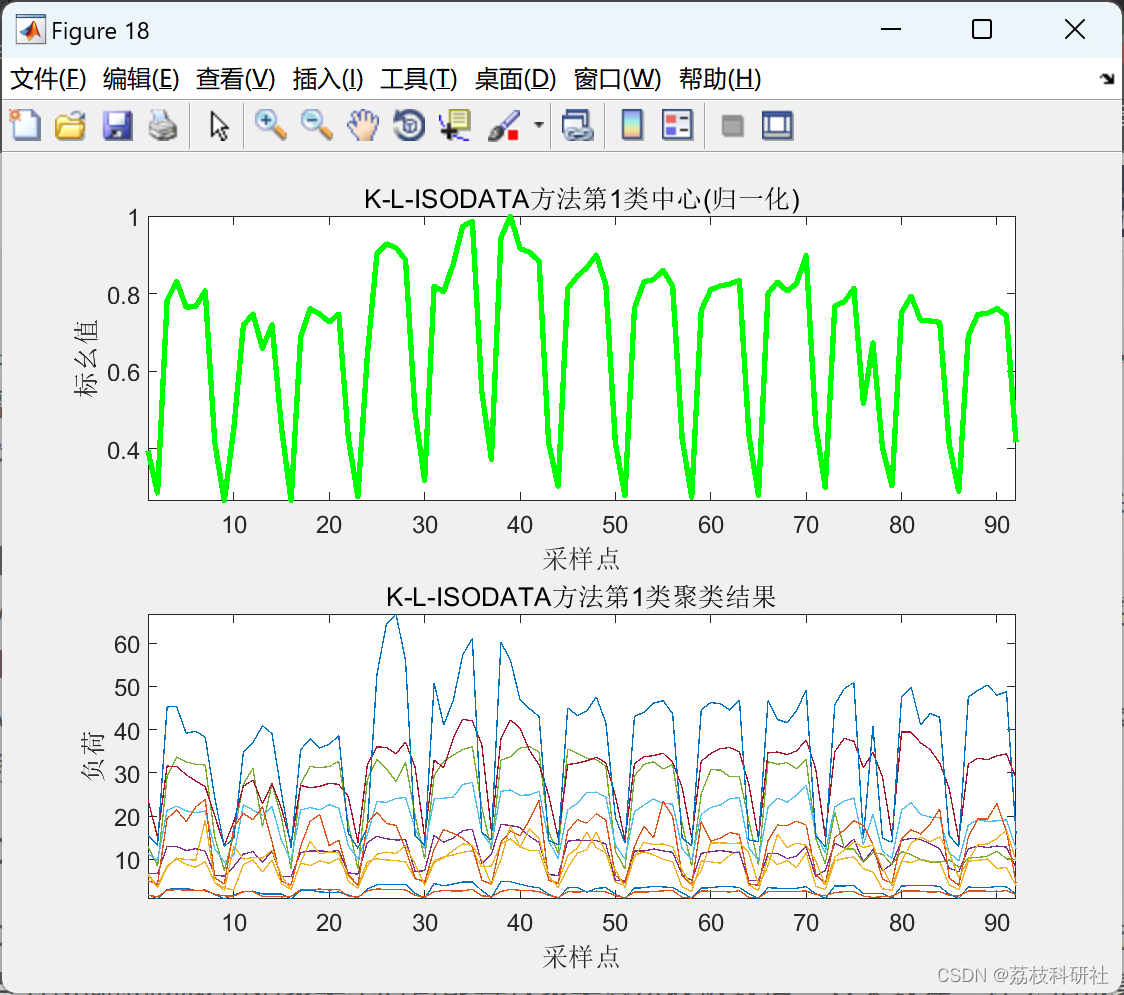

2.3 L-ISODATA聚类算法
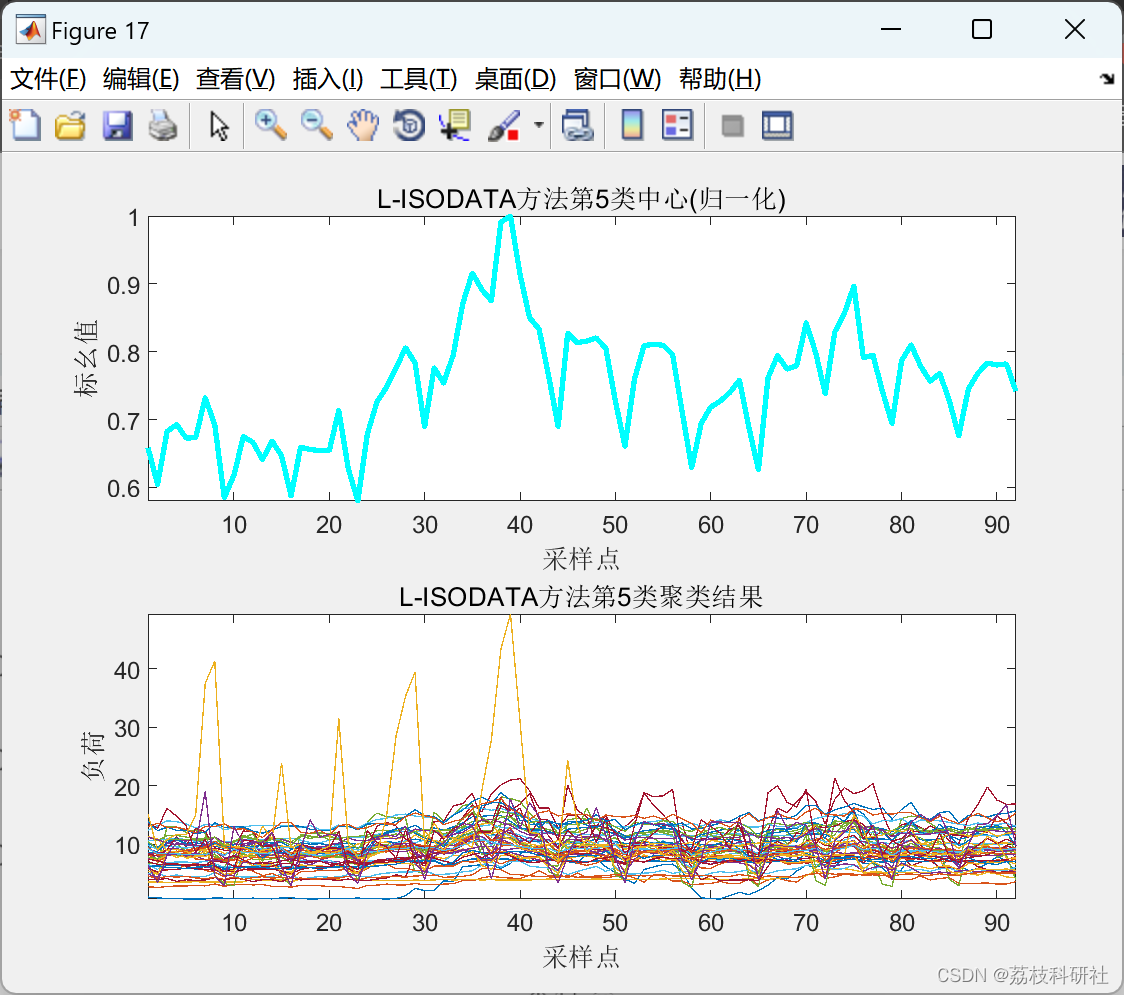

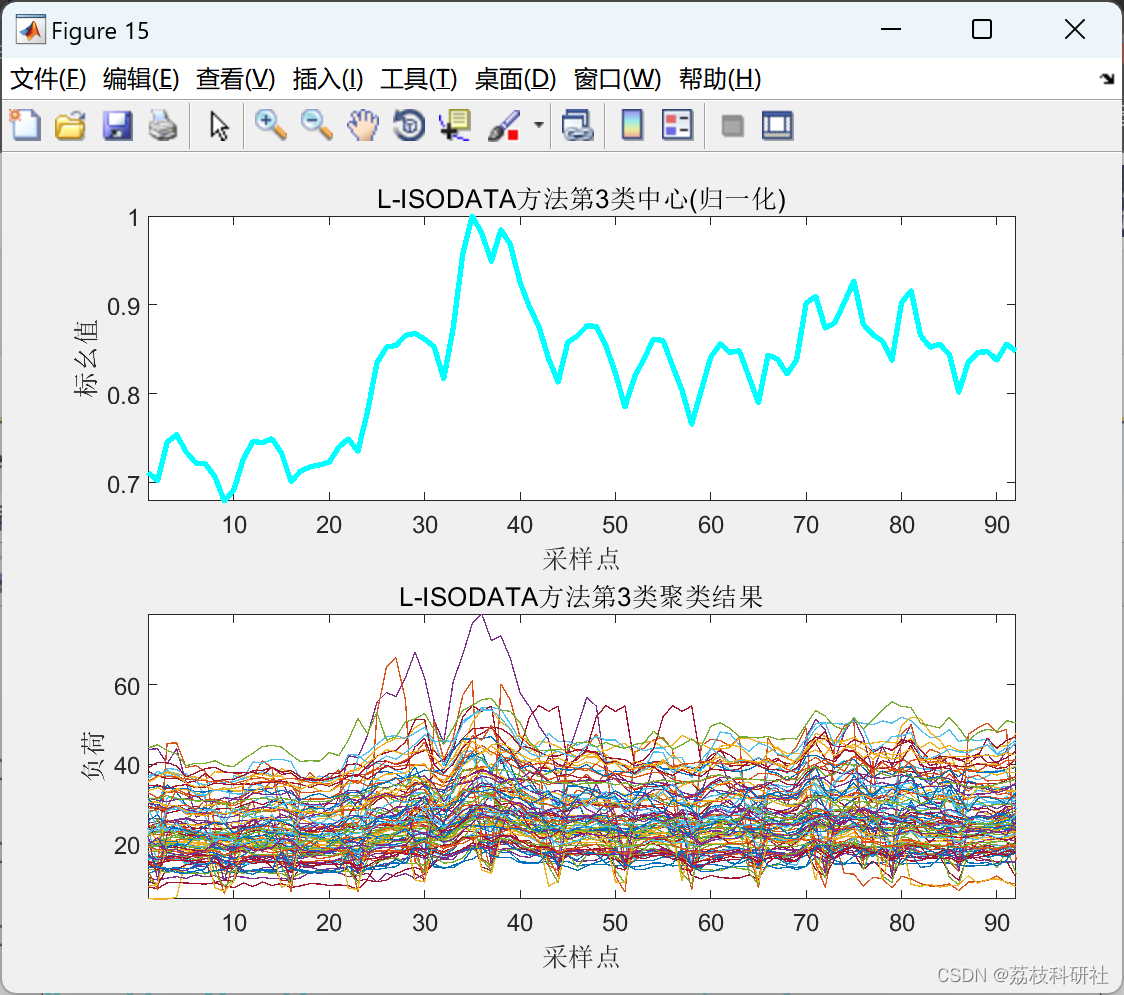

2.4 ISODATA聚类算法
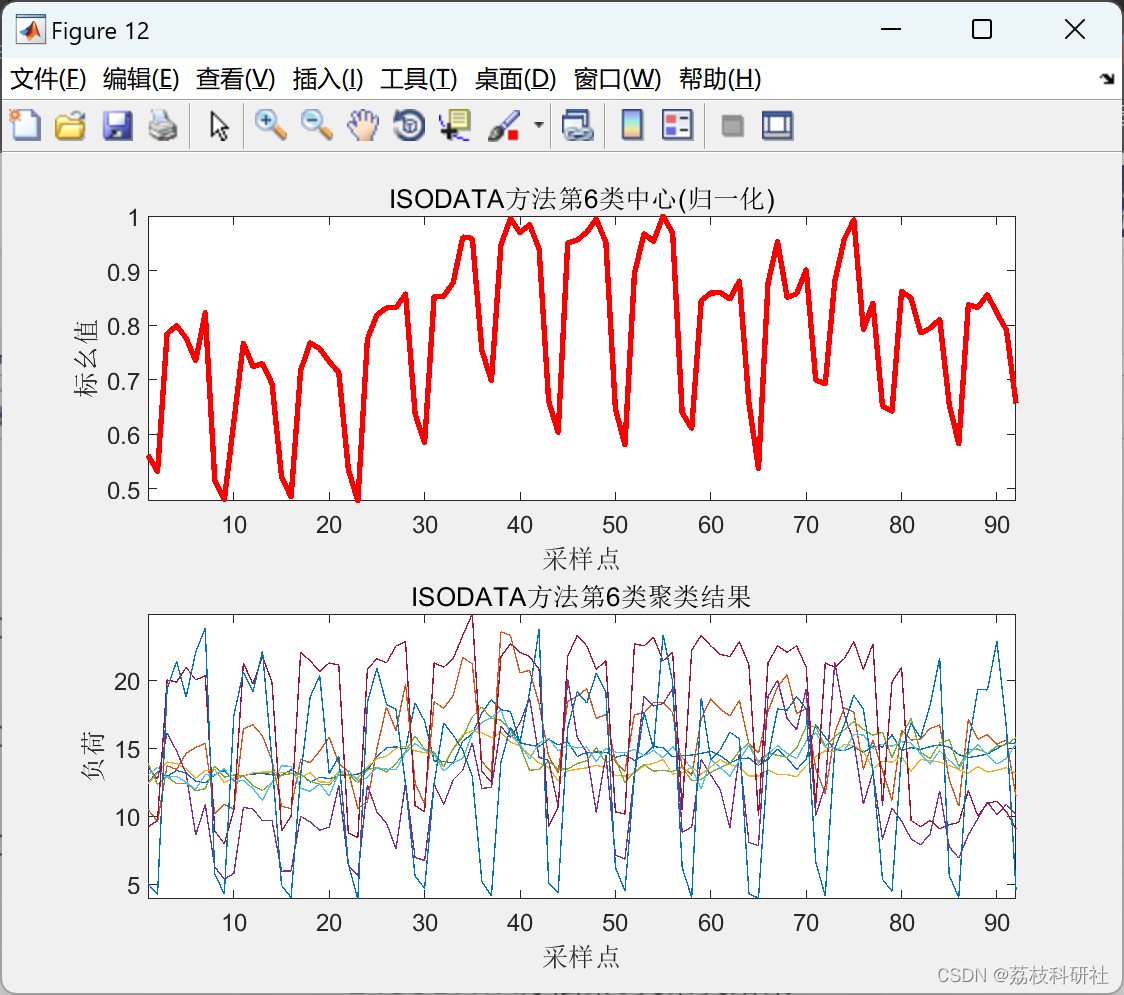

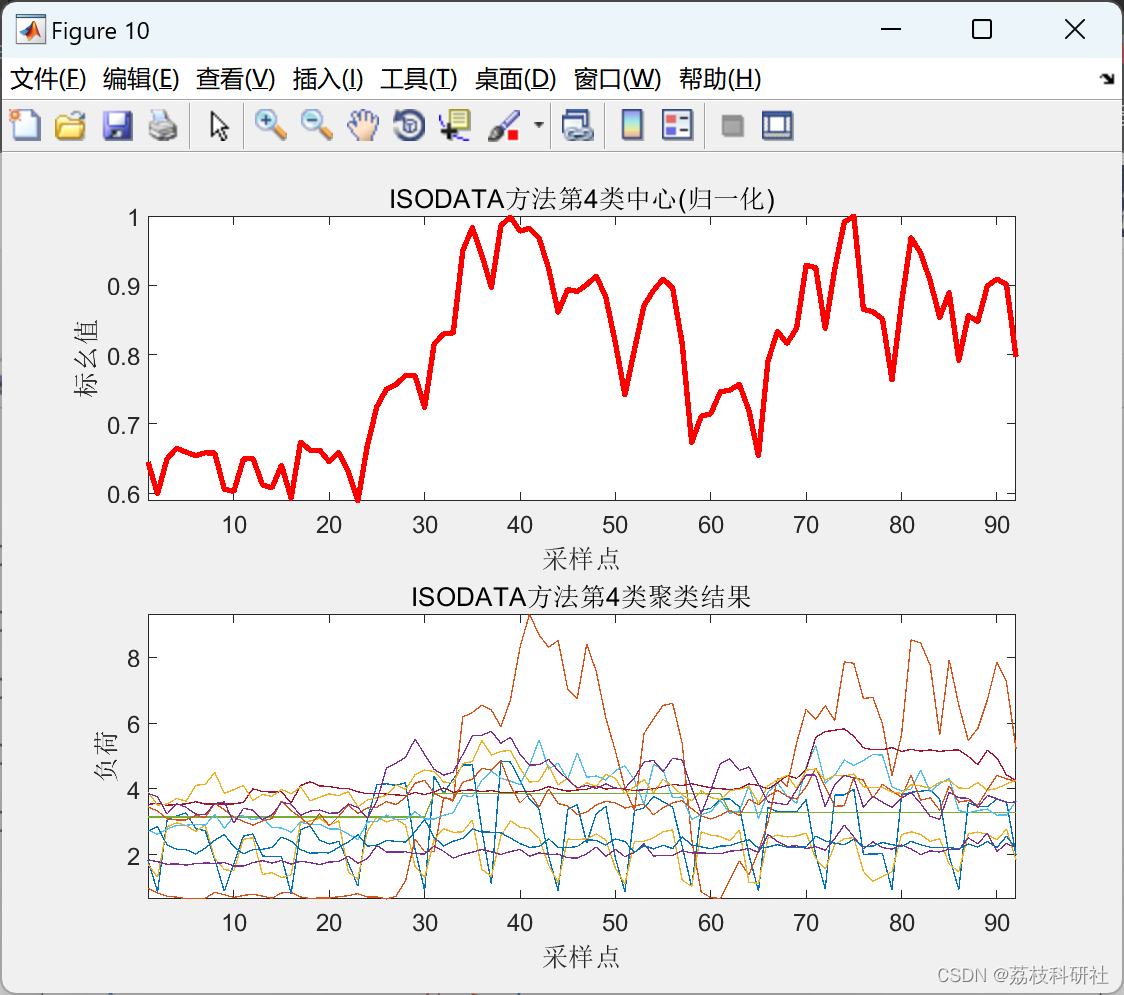

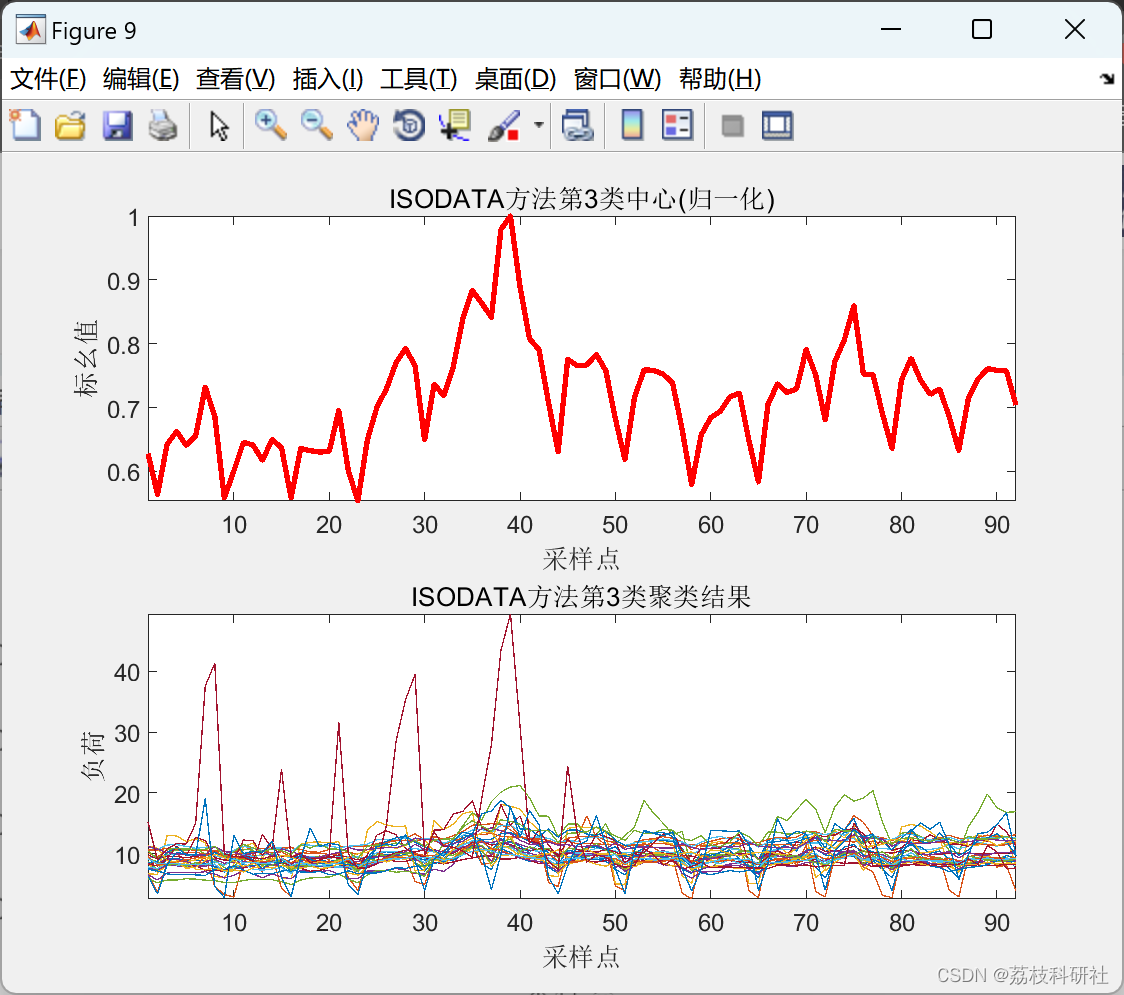

2.5 K-means聚类算法
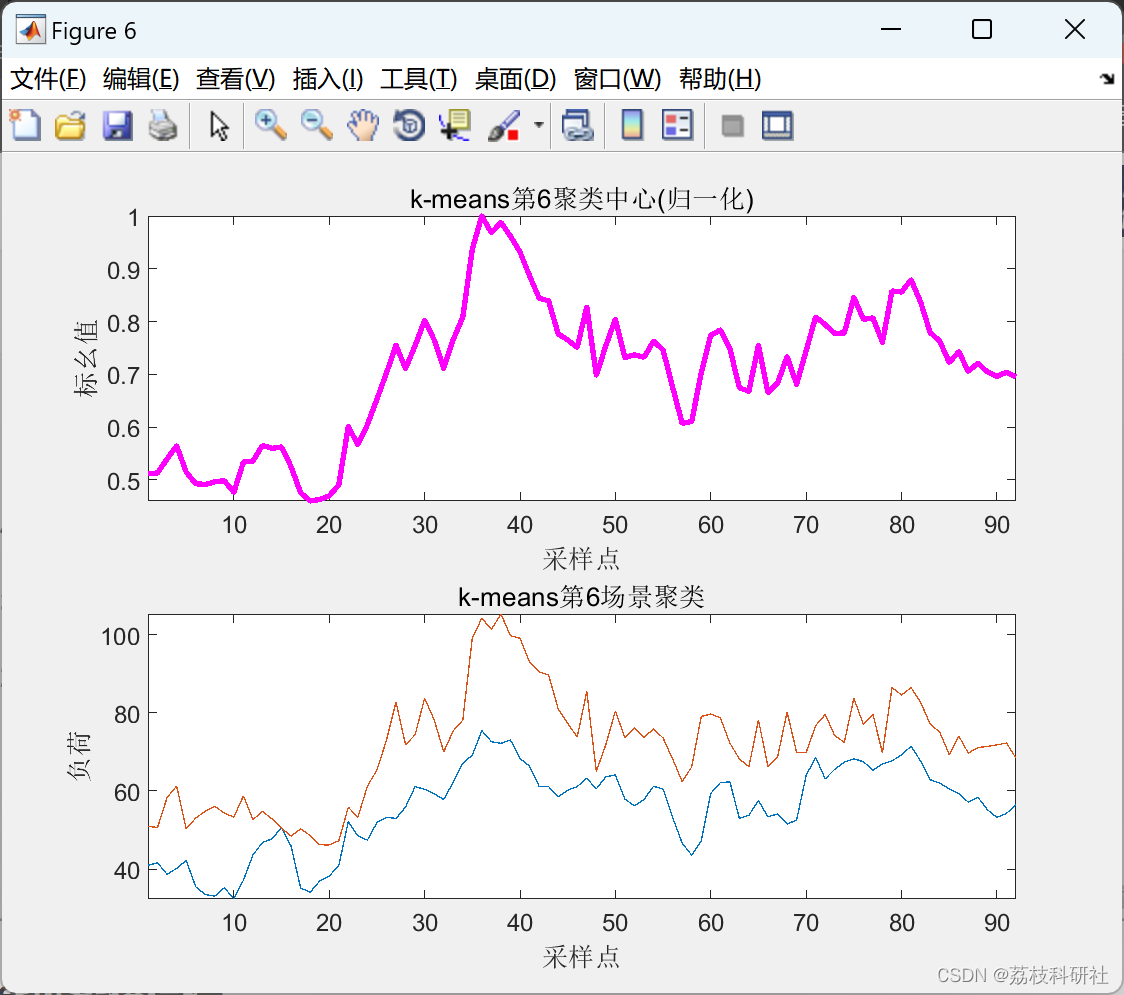

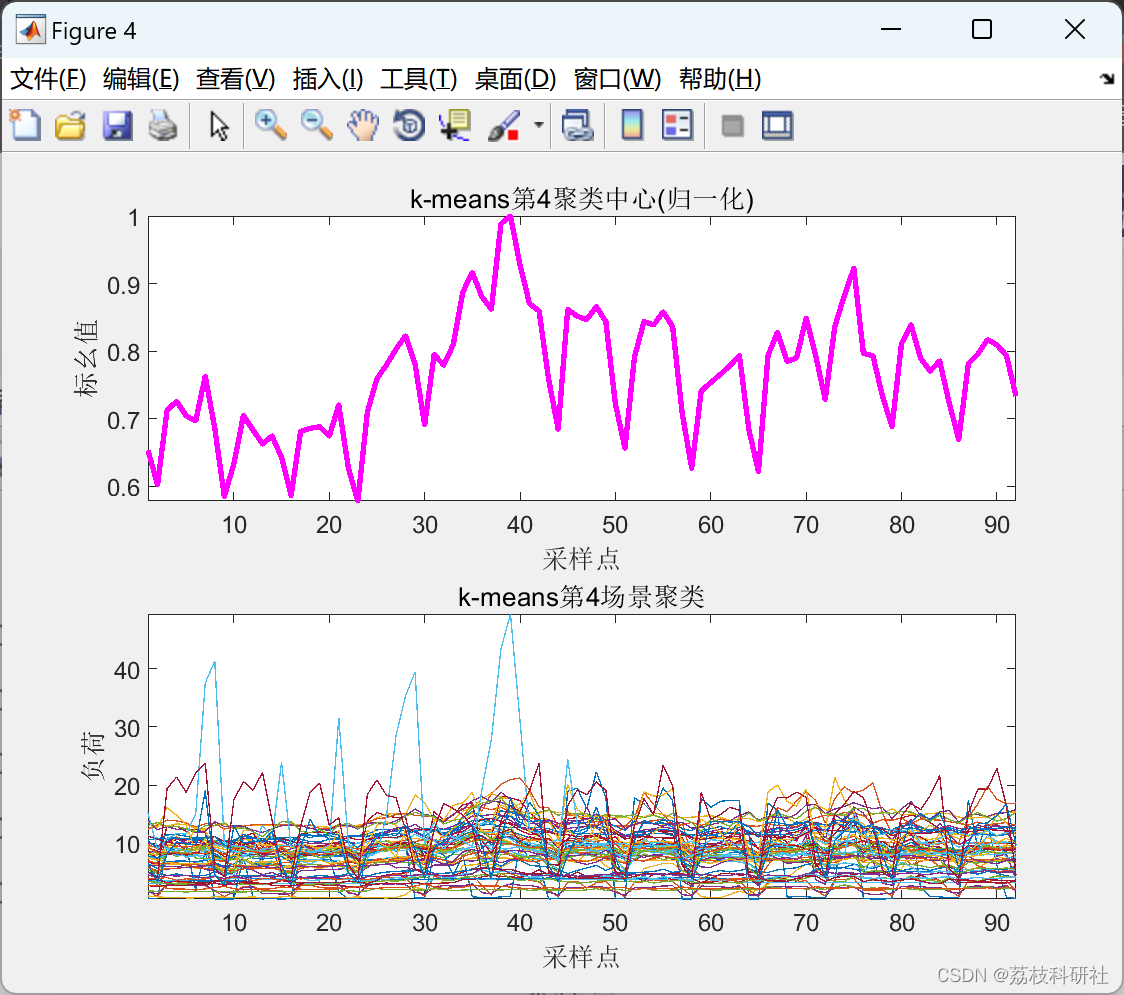

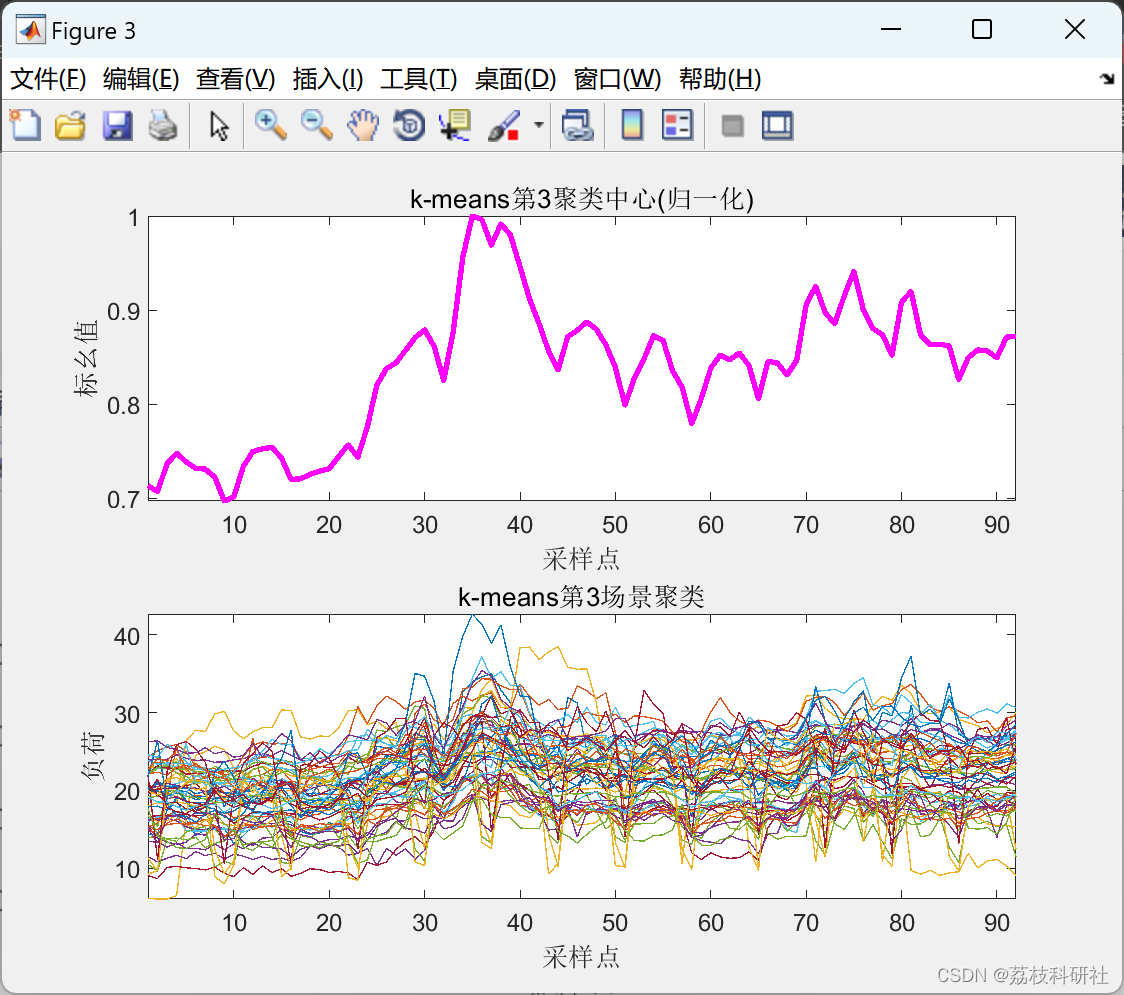

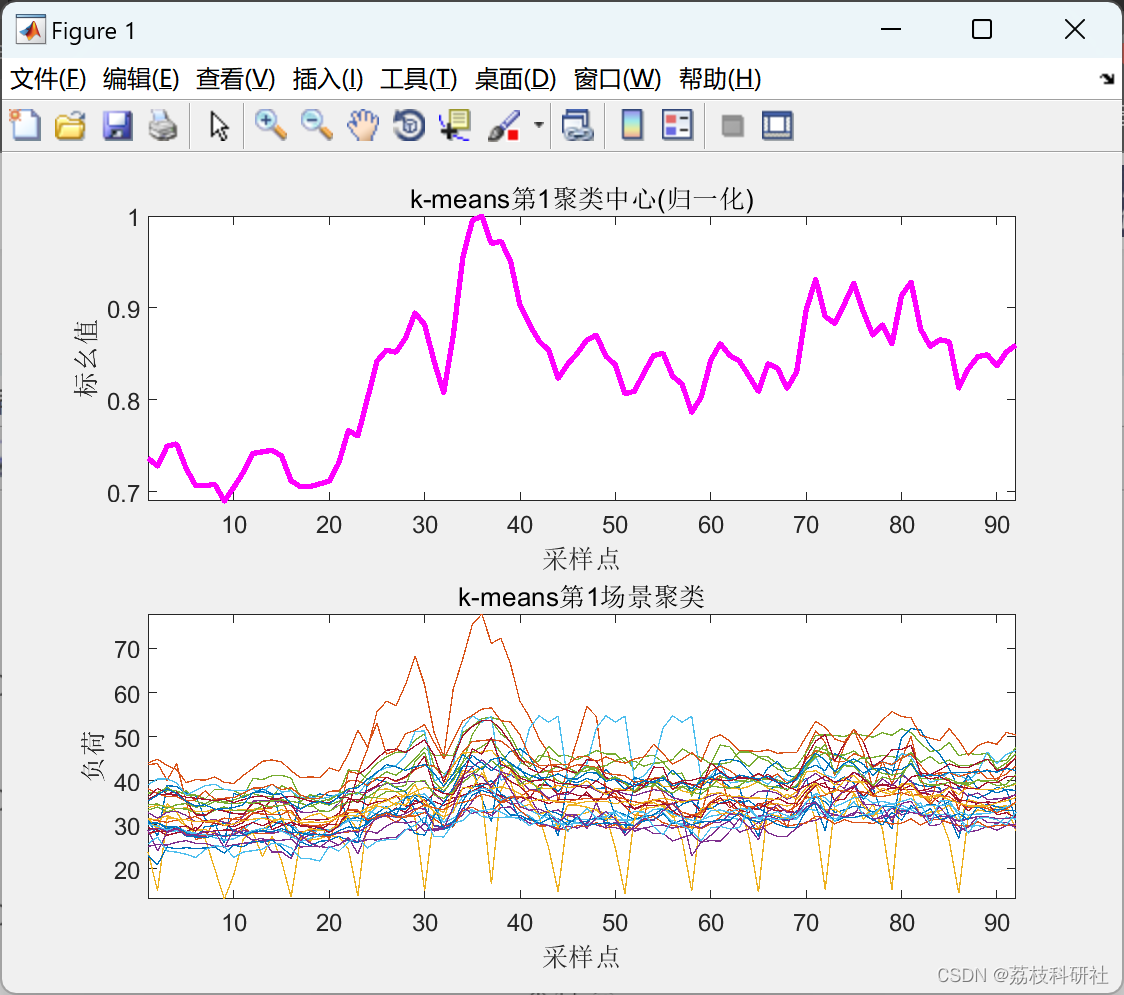

以上仅展现部分结果图。
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]张辰睿. 基于机器学习的短期电力负荷预测和负荷曲线聚类研究[D].浙江大学,2021.DOI:10.27461/d.cnki.gzjdx.2021.000300.