数组排序详解
- 1、排序算法小结
- 2、排序算法原理及实现
- 2.1 归并排序
- 2.2 快速排序
- 2.3 冒泡排序
- 2.4 插入排序
- 2.5 选择排序
- 2.6 希尔排序:
1、排序算法小结
排序算法可以分为两大类:
(1)非线性时间排序算法:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此称为非线性时间比较类排序。这类算法包括:冒泡排序、插入排序、选择排序、希尔排序、归并排序、快速排序、堆排序。
(2)线性时间非比较类排序算法:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序。 这类算法包括:桶排序、计数排序、基数排序。不过,虽然这几种算法的时间复杂度比较低,但是他们对要排序的数据要求也比较苛刻。
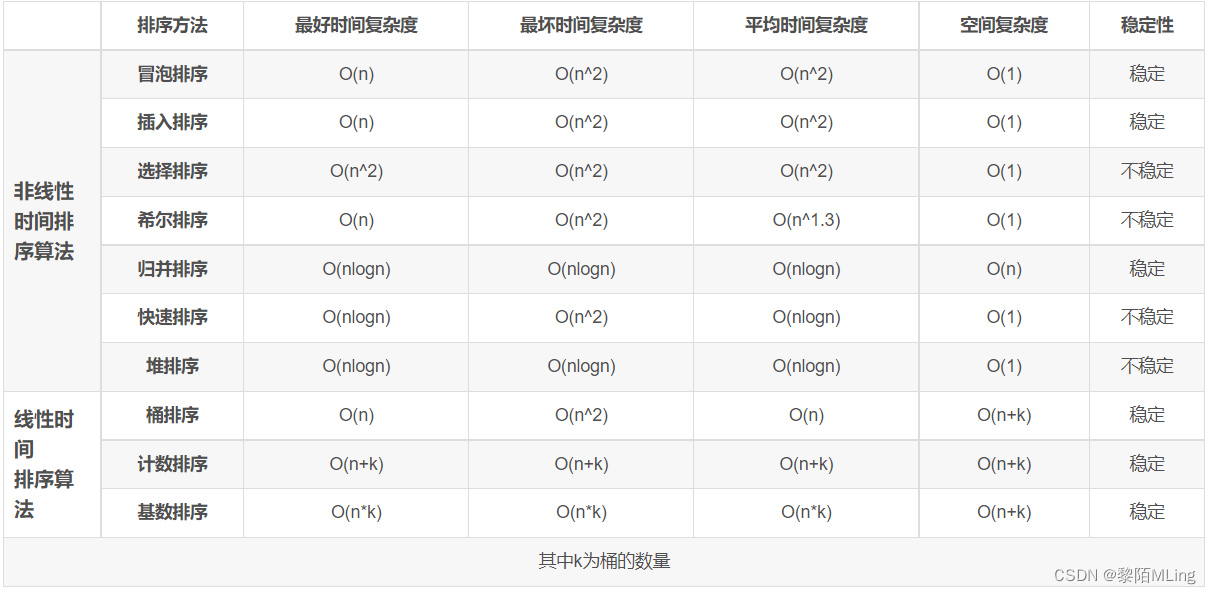
不同算法的复杂度分析如下:
2、排序算法原理及实现
2.1 归并排序
- 原理
归并排序的采用分治思想,如果要排序一个数组,我们先把数组从中间分成前后两个部分,然后对前后两个部分分别进行排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。核心是merge()合并函数。 - 实现
/**
* 归并排序:
* 采用分治思想,如果要排序一个数组,我们先把数组从中间分成前后两个部分,
* 然后对前后两个部分分别进行排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
* @author mling
*/
public class mergeSortTest {
public static void main(String[] args) {
int[] arr = new int[]{1,3,2,5,3};
mergeSort(arr,0,arr.length-1);
print(arr);
}
/**归并算法:
* @param arr 数组
* @param l 待排序的起始下标(左边)
* @param r 待排序的终止下标(右边)
* */
public static void mergeSort(int[] arr,int l,int r){
if(l >= r){//递归终止条件
return;
}
int mid = (l+r)/2;//取数组的中间点
mergeSort(arr,l,mid);//对数组前半部分进行排序
mergeSort(arr,mid+1,r);//对数组后半部分进行排序
merge(arr,l,r,mid);//合并数组前半部分和后半部分
}
/**
* 合并数组前半部分和后半部分: 从小到大
* //l为起点,r为终点,mid为第1区间与第2区间的分界线
*/
private static void merge(int[] arr, int l, int r, int mid) {
//初始化变量:i表示前半部分的下标,j表示后半部分的下标,k表示临时数组的下标
int i=l,j=mid+1,k=0;
int[] tmp = new int[r-l+1];
while(i<=mid && j<=r){//1,2区间均未结束
if(arr[i] <= arr[j]){//1区间的数<2区间
tmp[k++] = arr[i++];
}else{
tmp[k++] = arr[j++];
}
}
//将剩余数据拷贝到临时数组中
for(;i<=mid;i++) tmp[k++]=arr[i];
for(;j<=r;j++) tmp[k++]=arr[j];
//将tmp临时数组拷贝回原数组
for(int x=0;x<r-l+1;x++){
arr[l+x]=tmp[x];
}
}
private static void print(int[] arr) {
for(int i=0; i<arr.length; i++){
System.out.print(arr[i]);
}
System.out.println();
}
}
- 算法分析
(1)归并排序是一种稳定的排序算法;
(2)最好、最坏、平均时间复杂度都是O(nlogn)。
(3)空间复杂度是O(n),所以不是原地排序。这也是归并排序的一个致命弱点。
2.2 快速排序
- 原理
快速排序也是利用分治思想。如果要排序一组数据,我们先选择这组数据中任意一个数据作为分区点pivot,然后遍历这组数据,将小于分区点pivot的放到左边,大于分区点pivot的放到右边,将pivot放到中间。然后再分别对左右两部分进行排序。核心是partition()函数。 - 实现
/**
* 快速排序
* @author rmling
*/
public class QuickSortTest {
public static void main(String[] args) {
int[] arr = new int[]{1,3,2,5,3};
quickSort(arr,0,arr.length-1);
print(arr);
}
/**快速排序算法:从小到大
* @param arr:数组 l:待排序的起始下标(左边) r:待排序的终止下标(右边)
* */
public static void quickSort(int[] arr,int l,int r){
if(l >= r){//递归终止条件
return;
}
int part = partition(arr,l,r);//获取分区点
quickSort(arr,l,part-1);//对左分区进行排序
quickSort(arr,part+1,r);//对右分区进行排序
}
/**返回分区点下标*/
private static int partition(int[] arr, int l, int r) {
int i=l;int prv=arr[r];
for(int j=l;j<=r;j++){
if(arr[j] < prv){
swap(arr,i,j);
i++;
}
}
swap(arr,i,r);
return i;
}
private static void swap(int[] a,int x,int y){
int temp=a[x];
a[x]=a[y];
a[y]=temp;
}
private static void print(int[] arr) {
for(int i=0; i<arr.length; i++){
System.out.print(arr[i]);
}
System.out.println();
}
}
- 算法分析
(1)快速排序是一种原地排序,空间复杂度为O(1)。
(2)快速排序是一种不稳定算法。
(3)快速排序的最好时间复杂度、平均时间复杂度为O(nlogn)。但是在极端情况下,如果数组中的数据原来就是有序的,比如1,3,5,6,8,如果我们每次选择最后一个元素作为pivot,那每次分区得到的两个区间就是不均等的,我们需要大约进行n次分区操作,才能完成快排的整个过程,每次分区我们平均要扫描大约n/2个元素,这时时间复杂度为O(n^2),也就是最坏时间复杂度。
归并与快排的区别:
(1)归并排序和快速排序都是用分治的思想,代码都是通过递归来实现的,但是归并排序的核心是merge()合并函数,而快速排序的核心是partition()分区函数。归并排序的处理过程是从下到上,先处理子问题,然后再合并。而快速排序的处理过程正好相反,它的处理过程是从上到下的,先分区,然后再处理子问题。
(2)归并排序算法是一种任何情况下时间复杂度都比较稳定的排序算法,时间复杂度都是O(nlogn);快速排序算法最坏情况下时间复杂度为O(n^2) ,但是平均时间复杂度都是O(nlogn),不仅如此,快速排序时间复杂度退化到O(n^2)的概率非常小,我们可以通过合理选择pivot来避免这种情况。
(3)归并排序不是原地排序算法,空间复杂度比较高,为O(n);快速排序是原地排序算法,空间复杂度为O(1)。
(4)归并排序是稳定的算法,快速排序不稳定。
2.3 冒泡排序
- 原理
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系的要求。如果不满足就让它俩互换位置。一次冒泡会让至少一个元素移动到它应该在的位置,重复n次,就完成了n个数据的排序工作。 - 算法描述
(1)比较相邻的元素。如果第一个比第二个大,就交换它们两个;
(2)对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
(3)针对所有的元素重复以上的步骤,除了最后一个;
重复步骤1~3,直到排序完成。 - 实现
/**
* 冒泡排序
* @author mling
*/
public class BubbleSortTest {
public static void main(String[] args) {
int[] arr = new int[]{1,3,2,5,3};
bubbleSort(arr);
print(arr);
}
/**从小到大排序 */
public static void bubbleSort(int[] arr){
int len = arr.length;
for(int i=0; i<len; i++){
boolean flag = false;//提前退出冒泡循环的标志
for(int j=0;j<len-i-1;++j){
if(arr[j] > arr[j+1]){
swap(arr,j,j+1);
flag=true;//true表示有数据交换
}
}
if(!flag) break;//没有数据交换,提前退出
}
}
private static void swap(int[] a,int x,int y){
int temp=a[x];a[x]=a[y];a[y]=temp;
}
private static void print(int[] arr) {
for(int i=0; i<arr.length; i++){ System.out.print(arr[i]);}
System.out.println();
}
}
- 算法分析
(1)冒泡的过程中只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为O(1),是一个原地排序算法。
(2)冒泡排序是稳定的排序算法。
(3)最好时间复杂度为O(n),最坏时间复杂度为O(n*n),时间复杂度为O(n*n).
2.4 插入排序
- 原理
将数组的数据分为两个区间,已排序区间和未排序区间。初始已排序区间只有一个元素,就是数组的第一个元素。算法的核心思想就是,取未排序区间中的元素,在已排序区间中找到合适的位置将其插入,并保证已排序区间的数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。 - 算法描述
(1)从第一个元素开始,该元素可以认为已经被排序;
(2)取出下一个元素,在已经排序的元素序列中从后向前扫描;
(3)如果该元素(已排序)大于新元素,将该元素移到下一位置;
(4)重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
(5)将新元素插入到该位置后;
(6)重复步骤2~5。 - 实现
/**
* 插入排序
* @author mling
*/
public class InsertSortTest {
public static void main(String[] args) {
int[] arr = new int[]{1,3,2,5,3};
insertSort(arr);
print(arr);
}
/**从小到大排序 */
public static void insertSort(int[] arr){
int len = arr.length;
for(int i=1; i<len; i++){
int current = arr[i];
//查找需要插入的位置
int j=i-1;
for(;j>=0;j--){
if(arr[j] > current){
arr[j+1]=arr[j];
}else{
break;
}
}
arr[j+1] = current;
}
}
private static void print(int[] arr) {
for(int i=0; i<arr.length; i++){
System.out.print(arr[i]);
}
System.out.println();
}
}
- 算法分析
(1)插入算法的运行只需要用到一个额外的额存储空间,所以空间复杂度为O(1),是原地排序算法。
(2)插入算法是稳定的排序算法。
(3)最好时间复杂度为O(n),最坏时间复杂度为O(n*n),平均时间复杂度为O(n^2)。
2.5 选择排序
- 算法原理:
选择排序的实现思路和插入排序类似,也分为已排序区间和未排序区间。但是选择排序每次会从未排序区间中选择最小(最大)的元素,存放已排序区间的末尾。重复此操作,直到所有元素排序完毕。 - 算法描述:
(1)初始状态:无序区为R[1…n],有序区为空;
(2)第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
(3)n-1趟结束,数组有序化了。 - 算法实现:
/**
* 插入排序
* @author mling
*/
public class SelectSortTest {
public static void main(String[] args) {
int[] arr = new int[]{1,3,2,5,3};
selectionSort(arr);
print(arr);
}
/**选择排序:从小到大*/
public static void selectionSort(int[] arr){
int len = arr.length;
int minIndex;
for(int i=0;i<len;i++){
minIndex=i;
//寻找未排序部分的最小值的索引
for(int j=i+1;j<len;j++){
if(arr[j]<arr[minIndex]){
minIndex=j;
}
}
swap(arr,i,minIndex);
}
}
private static void swap(int[] a,int x,int y){
int temp=a[x];a[x]=a[y];a[y]=temp;
}
private static void print(int[] arr) {
for(int i=0; i<arr.length; i++){
System.out.print(arr[i]);
}
System.out.println();
}
}
- 算法分析:
(1)选择排序的空间复杂度为O(1),是一种原地排序算法。
(2)选择排序不是一种稳定的排序算法。因为选择排序每次都要从未排序区间中选择最小值,并和前面的元素交换位置,这样会破坏稳定性。
(3)选择排序的最好、最坏、平均时间复杂度都是O(n^2)。
2.6 希尔排序:
- 算法原理:
希尔排序是简单插入排序的改进版。他与插入排序的不同之处在于,它会优先比较较远的元素。希尔排序又叫缩小增量排序。希尔排序的核心在于间隔序列的设定(也就是增量)。既可以提前设定好间隔序列,也可以动态定义间隔序列。 - 算法描述:
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
(1)选择一个增量序列t1,t2,…,tk,其中ti>tj,i<j,tk=1;
(2)按增量序列个数k,对序列进行k 趟排序;
(3)每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m(m=length/ti) 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。 - 算法实现:
/**
* 希尔排序
* @author mling
*/
public class ShellSortTest {
public static void main(String[] args) {
int[] arr = new int[]{1,3,2,5,3};
shellSort(arr);
print(arr);
}
/**希尔排序:从小到大*/
public static void shellSort(int[] arr){
int len = arr.length;
int gap=1;//希尔排序的关键在于设置增量,这里我们动态设置一个增量
while(gap<len/3){
gap=gap*3+1;
}
int temp;
for(;gap>0;gap=(int) Math.floor(gap/3)){
for(int i=gap;i<len;i++){
temp = arr[i];
int j=i-gap;
for(;j>=0 && arr[j]>temp;j-=gap){
arr[j+gap]=arr[j];
}
arr[j+gap]=temp;
}
}
}
private static void print(int[] arr) {
for(int i=0; i<arr.length; i++){
System.out.print(arr[i]);
}
System.out.println();
}
}
- 算法分析:
(1)希尔排序的空间复杂度为O(1),是一种原地排序算法。
(2)希尔排序不是一种不稳定的排序算法。多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以希尔排序是不稳定的。
(3)选择排序的最好时间复杂度为O(n)、最坏时间复杂度都是O(n*n),平均时间复杂度为O(n^1.3)。
参考链接: 排序算法