参考文献如上。
双层优化问题是一类具有挑战性的优化问题,包含两个层次的优化任务。在这些问题中,下层问题的最优解成为上层问题的可能可行候选。这样的要求使得优化问题难以解决,并使研究人员忙于设计能够有效处理该问题的方法。尽管付出了努力,但几乎没有任何有效的方法能够处理复杂的双层问题。本文介绍了基于最优下层变量相对于上层变量的二次近似的双层进化算法。该方法能够在相对较少的函数求值中处理具有不同复杂性的两层问题。来自经典优化的思想已经与进化方法混合,为一大类双层问题生成了一个有效的优化算法。在两组测试问题上对算法的性能进行了评估。第一组是最近提出的SMD测试集,其中包含复杂性可控的问题,第二组包含从文献中收集的标准测试问题。已经将所提出的方法与三个基准进行了比较,并且观察到性能增益是显著的。与论文相关的代码可以从网站上获取。
双层优化是优化的一个分支,它包含一个嵌套在外部优化问题约束下的优化问题。外部优化任务通常被称为上层优化问题,内部优化任务被称为下层优化问题。下层问题作为约束出现,使得只有下层优化问题的最优解才是上层优化问题的可能可行候选。这样的要求使得两级优化问题难以处理,并使研究人员和实践者同样忙碌。分层优化结构可能会带来一些困难,如非凸性和不可连接性,甚至对于更简单的两层优化,如两层线性规划问题。已知双层线性规划是强NP难的(汉森,贾马尔,萨瓦德,1992),已经证明,仅仅评估最优解也是一个NP难的任务。这给了我们一个关于复杂(非线性、非凸、不连续等)的双层问题所带来的挑战的概念。)目标和约束函数。
本文中,我们提出了一种混合策略,它将经典双层规划的思想运用到进化算法中。已经讨论了一些现有的数学结果,作为设计进化算法的动机。该方法是一种基于下层最优变量的二次近似作为上层变量函数的双层进化算法。本文提出的算法不是针对可以用精确方法解决的问题,而是针对由于前面提到的现实困难而导致精确方法失败的问题。在我们的研究中选择的大多数测试问题不能用经典的双层规划算法来解决,另一方面,单独使用进化算法以嵌套的方式来解决它们将被证明在计算上非常昂贵。已经进行了计算研究来证明我们的主张。
双层优化是一个包含两层优化任务的嵌套优化问题。双层优化问题的结构要求下层优化问题的最优解只能作为上层优化问题的可行候选。
算法说明
我们将我们的算法称为基于二次近似(BLEAQ)的双层进化算法。该算法从包含随机上层变量的上层成员的初始种群开始。对于每个成员,使用较低级别的优化方案解决较低级别的优化问题,并记录最佳的较低级别成员。在得到的下层最优解的基础上,建立上层变量和下层最优变量之间的局部二次关系。如果近似值很好(根据均方误差 1 ),那么它可以用于预测任何给定的上层变量集的最优下层变量。这消除了解决较低级别优化问题的要求。然而,在接受二次逼近的最优解时需要谨慎,因为即使是单一的差解也可能导致错误的二阶最优解。在算法的每一代中,都会生成新的二次近似值,随着总体趋于真正的最优值而不断改进。在程序结束时,该算法不仅提供了双层问题的最优解,而且还提供了表示接近最优值的上下变量之间关系的可接受的精确函数。
步骤:
- 初始化:算法从大小为 N 的种群开始,通过随机生成所需数量的上层变量进行初始化,然后执行下层进化优化程序以确定相应的最优下层变量。 适应度是根据上层函数值和约束来分配的
- 标记:将所有上层成员标记为 1,其中已经成功进行了下层优化运行,其他标记为 0。
3.上层父代的选择:从当前N大小的人群中,选择最好的标签1成员作为父代2之一。从当前人口中随机选择2(μ1)名成员,并根据上层适应值进行锦标赛选择,以选择剩余的μ1名家长。
4.上层进化:将最好的tag 1成员作为index parent,将上一步的成员作为其他parent。 然后,使用交叉和多项式变异算子从所选的 μ 父母创建 λ 后代。
5.评估后代:在这一步中,我们通过二次近似或执行较低级别的优化来确定后代的较低级别变量。 如果种群中标签 1 成员的数量大于 nc = (n +1)(n +2) 2 + n 并在后代周围形成一个凸包,则为该后代计算最佳较低水平 通过步骤 5a 的变量; 否则转至步骤 5b。
步骤 5a :
二次逼近:形成一个由 n c 最近的 3 个标签 1 成员组成的池,这些成员在二次逼近 4 的后代周围形成一个凸包。 使用选定的 n c 个成员来获得 ψ loc 的二次近似 ˆψ(详细信息请参阅第 5.1 节)。 使用二次近似来获得对应于后代的较低水平的变量。 如果近似的均方误差 e mse (参见第 5.1.1 节)小于参数 e 0 ,则认为二次近似是好的,后代标记为 1,否则标记为 0 .
步骤 5b :
下层优化:为了对后代成员执行下层优化,确定最接近的(再次使用上层变量根据欧几里德距离测量)标签 1 父代。 从最接近的标签 1 父级,复制较低级别的最佳成员( y ( c ) )(请参阅第 5.2 节)。 此后,使用以(y(c))为起点的二次规划方法对后代执行较低级别的优化。 如果二次规划不适用,请使用进化优化算法来解决问题。 复制的较低级别成员 ( y ( c ) ) 用作较低级别进化优化运行中的种群成员。 将后代标记为 1,其较低级别的优化成功终止。 结合每个后代的上层和下层变量(从步骤 5a 或 5b 获得)并找到其在上层的适应度。
6 种群更新:找到后代的较低级别变量后,从父种群中选择 r 个成员。 形成了一个由选定的 r 个成员和 λ 个后代组成的池。 池中最好的 r 个成员替换从总体中选择的 r 个成员。 执行终止检查(请参阅第 5.6 节)。 如果终止检查为假,则算法移至下一代(步骤 3)。
算例:
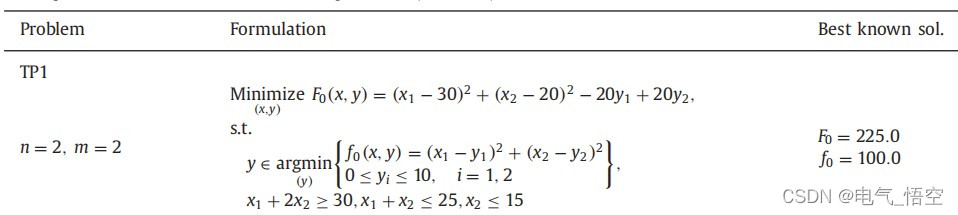
上层:
算例中,上层优化目标为:
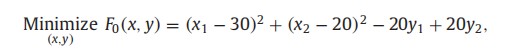
变量为:x1,x2,y1,y2
约束为:x1+2x2>=30
x1+x2<=25
x2<=15
0<=y1<=10
0<=y2<=10
下层:
算例中,下层优化目标为:
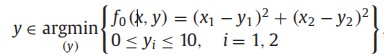
变量为:x1,x2,y1,y2
约束为:x1+2x2>=30
x1+x2<=25
x2<=15
0<=y1<=10
0<=y2<=10
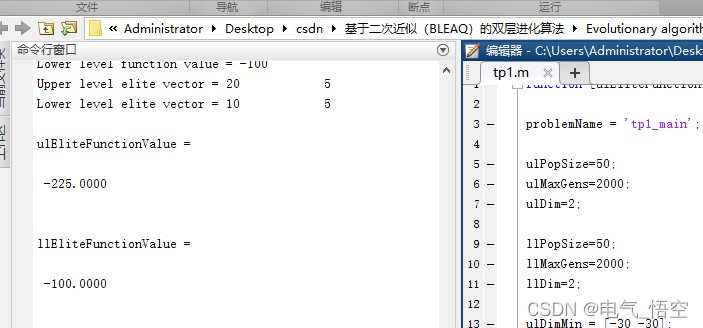
计算最优解结果:

程序如下:
部分程序:
ulPopSize=50; % Size of UL population
ulMaxGens=2000; % Maximum number of generations allowed at UL
ulDim=2; % Number of UL dimensions
llPopSize=50; % Size of LL population
llMaxGens=2000; % Maximum number of generations allowed at LL
llDim=2; % Number of LL dimensions
ulDimMin = [-30 -30]; % Minimum value accross UL dimensions
ulDimMax = [30 15]; % Maximum value accross UL dimensions
llDimMin = 0*ones(1,llDim); % Minimum value accross LL dimensions
llDimMax = 10*ones(1,llDim); % Maximum value accross LL dimensions
ulStoppingCriteria = 1e-4;
llStoppingCriteria = 1e-5;
。。。。。。。。。略详细程序转:https://download.csdn.net/download/weixin_47365903/76649200
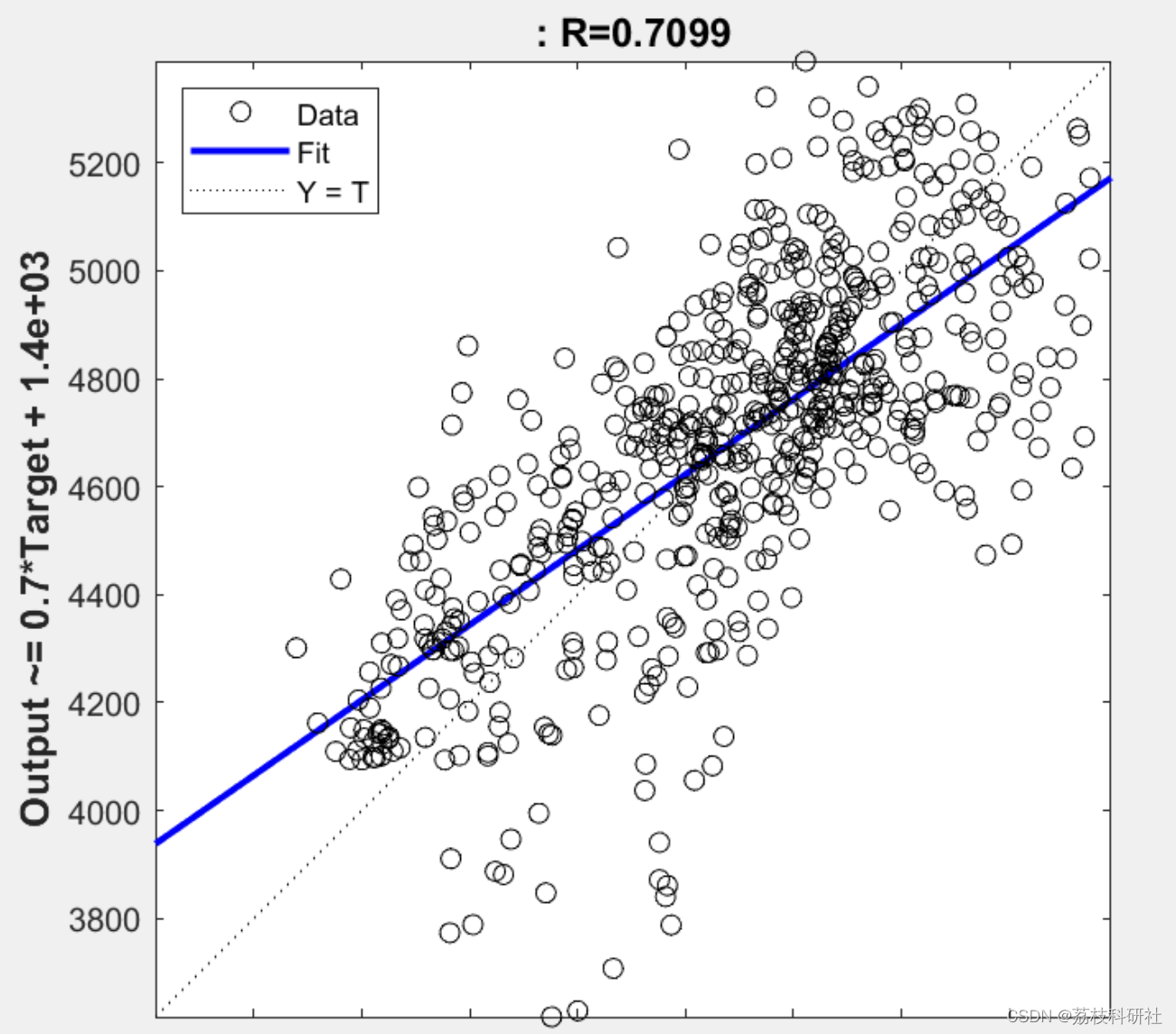
程序运算结果: