递归深度太深会栈溢出
程序是对的,但是递归个10000层就是栈溢出
int fun(int n)
{
if (n <= 1)
{
return n;
}
return fun(n - 1) + n;
}

所以需要非递归来搞快排和归并,在效率方面没什么影响,只是解决递归深度太深的栈溢出问题
有的能直接改,例如斐波那契,知道第一个第二个的迭代,有的需要辅助,直接改不了
斐波那契数列非递归
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}
快排 非递归
思路:看递归栈帧保存了什么,就是两个区间的下标,用栈来辅助改循环
栈没法一下入两个,非要搞可以弄一个结构体保存两个区间的下标,但那样太麻烦,简单点就是可以每次入一个,入两次栈,也要注意先入右区间下标再入左区间下标
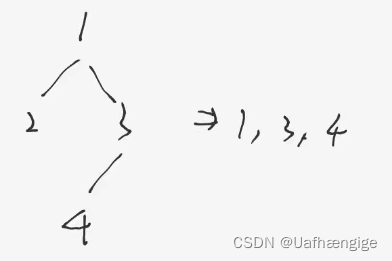
注意的就是区间入栈的顺序,先入右子树的区间,再入左子树,这样出栈时保证先序,并且正确模拟递归过程嘛
区间[0,9]单趟排选出一个key,就可以将[0,9]出栈,分出[begin, keyi-1] keyi [keyi+1, end]左右区间,左右区间如果只有一个值,或者区间不存在,就不需要再入栈了,不然就入栈,入栈顺序是右边区间先入栈,再左边入栈
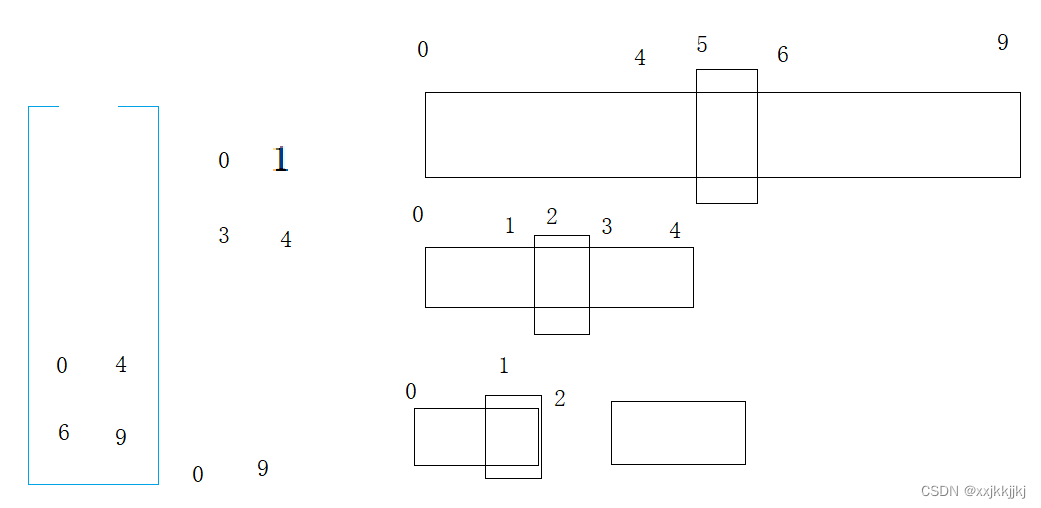
[0,9]出栈带入[0,4][6,9]继续出栈[0,4],选key单趟排,再入栈左右区间
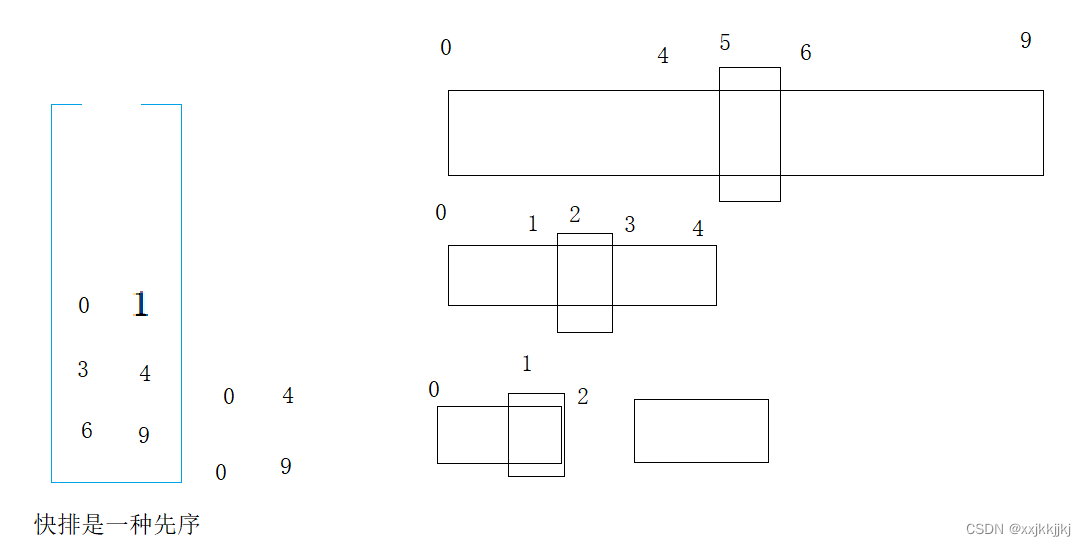
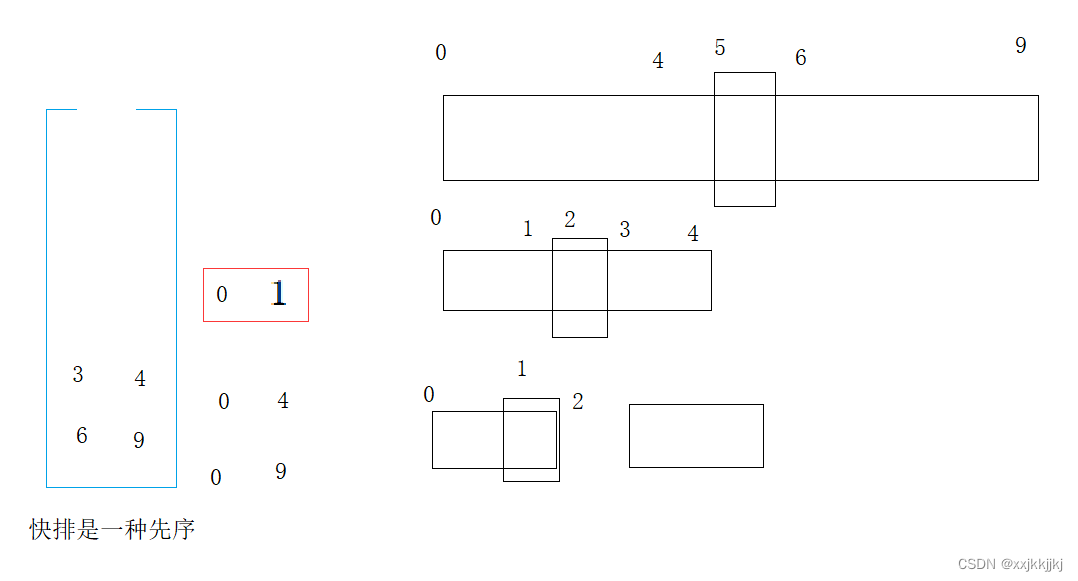

此时[0,1]出栈单趟选key后左右子区间不符合入栈条件,则继续出[3,4]
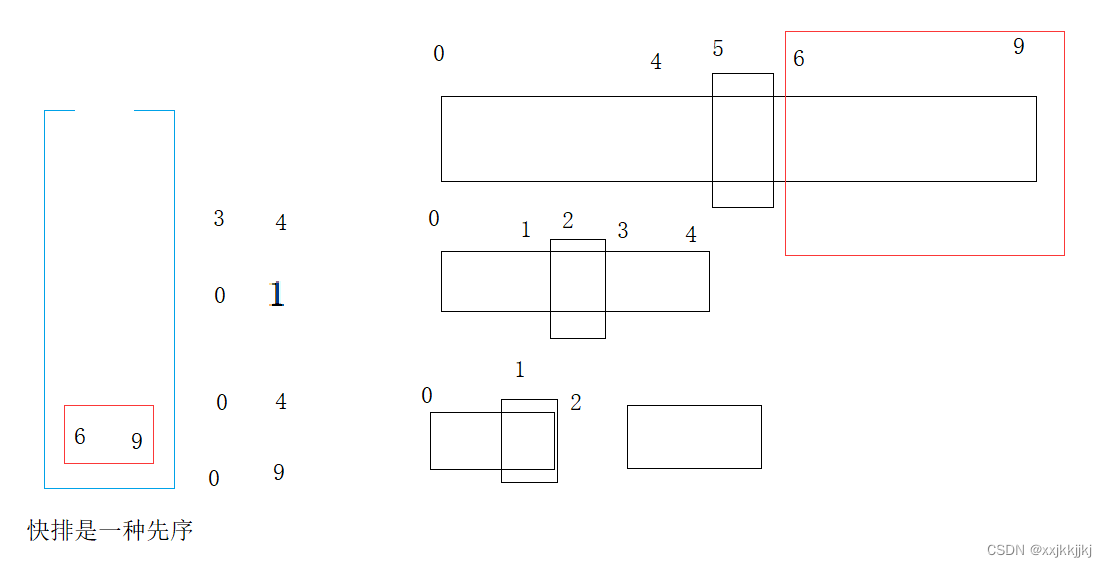
[3,4]处理完了就到了[6,9],再继续单趟,分左右区间…
如此循环下去,直到栈为空就结束
//非递归 效率和递归 无区别 只是解决了递归深度过高栈溢出
void QuickSortNonR(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
int keyi = PartSort3(a, begin, end);
//[begin, keyi-1] keyi [keyi+1, end]
if (keyi + 1 < end)
{
StackPush(&st, end);
StackPush(&st, keyi + 1);
}
if (begin < keyi-1)
{
StackPush(&st, keyi-1);
StackPush(&st, begin);
}
}
StackDestroy(&st);
}
归并排序
时间复杂度
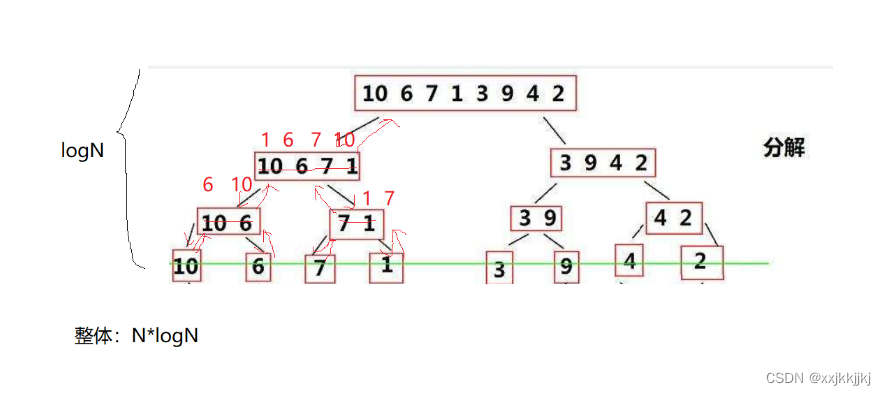
每层归并都是N,一共有logN层,就是O(NlogN)
思想
两个有序区间归并:
依次比较,小的尾插到新空间
前提是他们两个区间 都 有序
没序怎么办,平分变成子问题,继续让左区间有序,右区间有序
平分区间只有一个数,可以认为此时有序
开辟一个临时空间,将左区间1个数,右区间1个数归并,再拷贝回原数组
不开辟导致数据覆盖问题
左区间有序右区间有序再归并,这是后序
涉及开辟临时空间就需要在写一个子函数,不然每次递归调用自己都开辟空间
如何平分取中间下标也挺有意思
公式为 mid = (left + right) / 2。其中,left为左边界下标,right为右边界下标,mid为中间下标。
mid是左右边界的平均值,两个数加起来取个平均值嘛整形直接中间值,三数取中同理
结束条件是否有不存在的区间,还是只有一个数的情况呢?
根据递归图看出 只有[0,0][1,1]这种只有一个数的区间情况,并不存在不存在的区间
1.递归
递归过程-后序-先进入左子树,右子树,归并

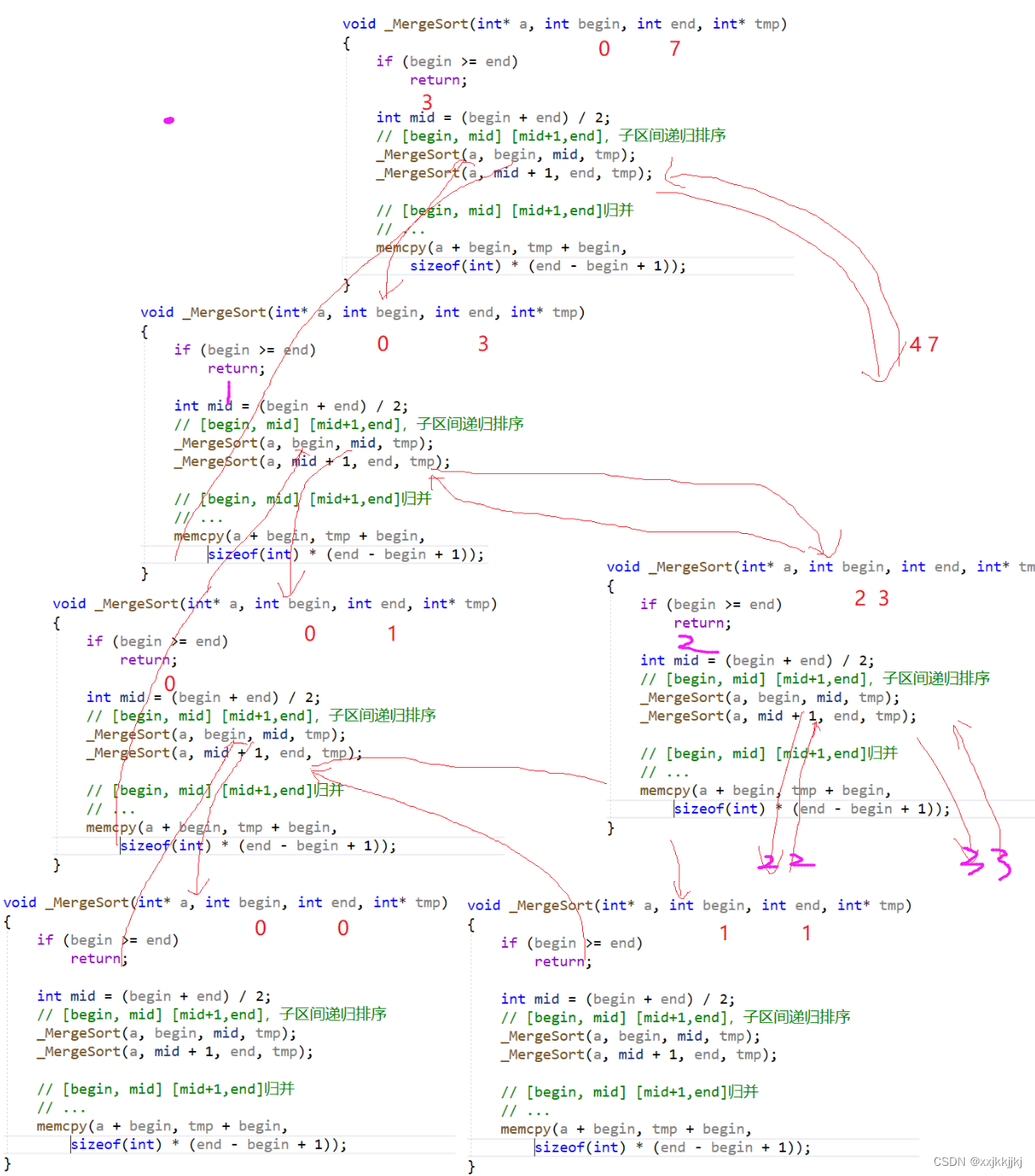
void _MergeSort(int* a, int left, int right,int* tmp)
{
if (left >= right)//不会有不存在的区间,这样写肯定没错
return;
int mid = (right + left) / 2;//左边界和右边界的平均值,整形直接中间值
//[left mid] [mid+1 right],子区间递归排序
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid+1, right, tmp);
int i = left;
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
//归并
//[begin1 end1] [begin2 end2]//涉及left right 建议设置局部变量,不直接使用left right
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a+left,tmp+left,sizeof(int)*(right-left+1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, 0, n - 1,tmp);
free(tmp);
}
注意i = left 和 memcpy(a+left,tmp+left,sizeof(int)*(right-left+1));
归并的区间在右边就不是从0 开始的,而是从left开始的,归并到tmp中也要归并到从left开始的位置,不可让i =0 会导致归并临时空间tmp都从0开始,调试时也不清晰。
2.非递归
归并排序 无法用栈保存区间 来搞非递归
因为归并后序 和快排栈辅助非递归的前序 顺序不一样,一开始的[0,9]上来就出栈了,归并排序后回到[0,9]你还得用[0,9]来归并,如果强行用栈来搞也不是不行,但是很困难,不建议
我们知道归并最后一层都是一个一个归并 再 两两归并,四四归并…
那就像类似斐波那契数列知道第一第二求第三
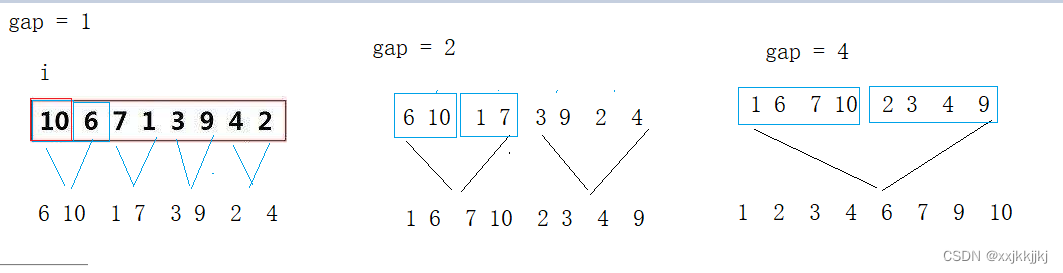
直接写循环控制,用gap来控制 gap = 1 gap =2 gap =4来11归,22归,44归
gap是归并过程中,每组数据个数
控制两组有序数组归并
如果数据个数不能如此平分达到11 22 44归并 必然会造成越界
又或者说数据个数不是2^n倍,但是先把符合的写出来
先弄出符合倍数的{ 10,6,7,1,3,9,4,2 }
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail\n");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//[begin1 end1] [begin2 end2]
printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
// 拷贝
}
printf("\n");
gap *= 2;
}
free(tmp);
}
不要过于依赖调试,调试适合看一些简单的情况,如果有多种组合情况,可以用printf()函数打印你想看的值
为了更好的看分组情况加了//[begin1 end1] [begin2 end2] printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);在控制这四个下标下面
符合2的n次方倍的分成功了,但是不符合的会越界,导致报错崩溃,但也没关系,这个printf()输出仍然能够输出,方便看分组情况
比如下面
不符合的并不是奇数偶数的问题,而是2的n次方倍的问题
当数据个数是偶数12,仍然越界
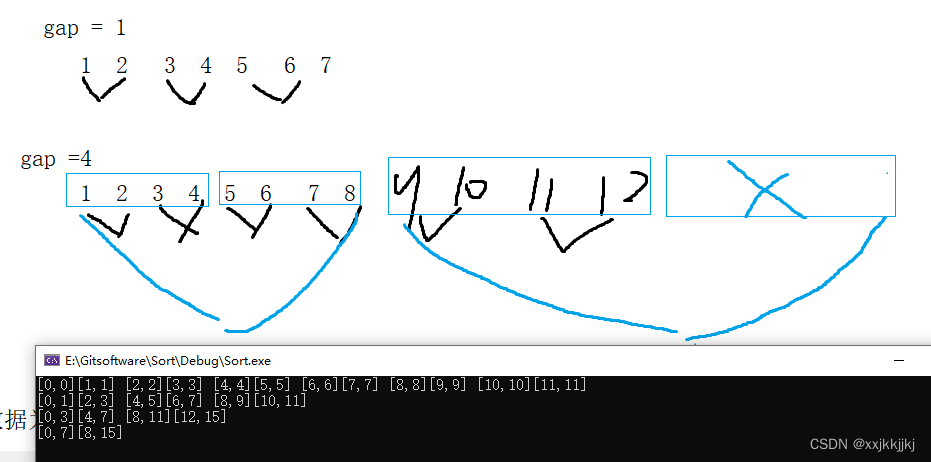
同样是偶数 但是不够分 达不到2^4 = 16 gap = 4的时候不够分,造成越界
那越界怎么办呢
更古不变的–复杂问题分解为简单问题:分类处理
刚刚12个数据的例子不太好,只是说明不是奇数偶数的问题
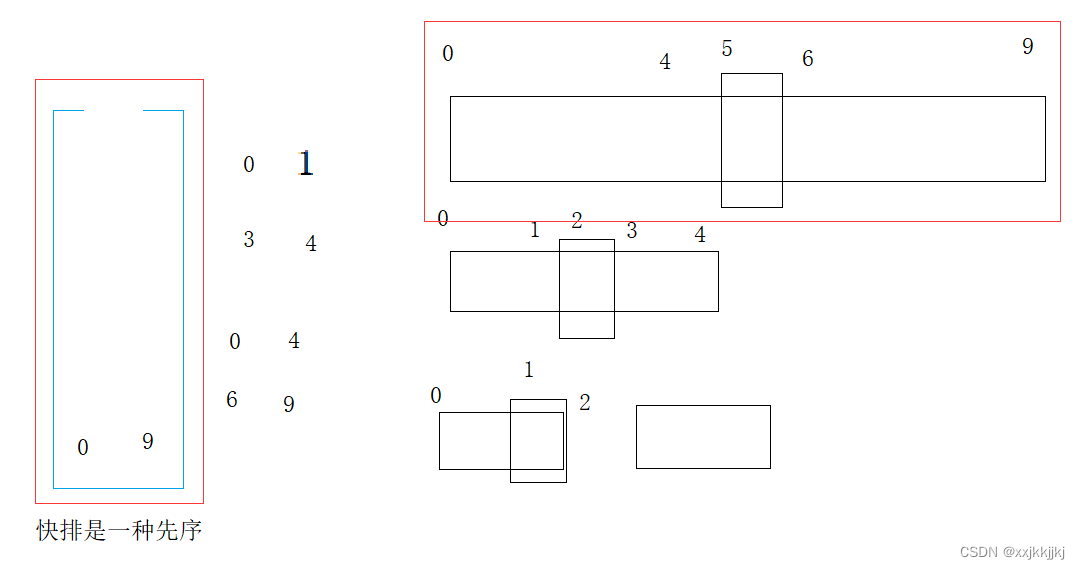
现在我们用9个数据,覆盖越界情况更广
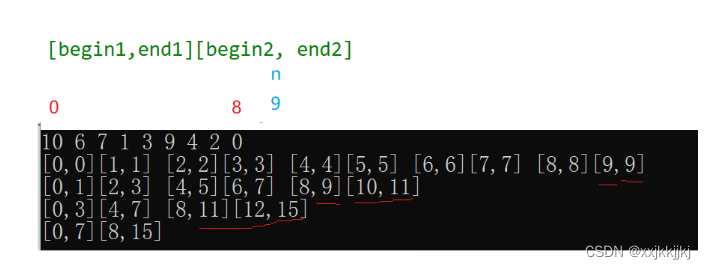
画红线的都是越界的区间
将复杂问题分解为简单问题:分类处理
三种情况
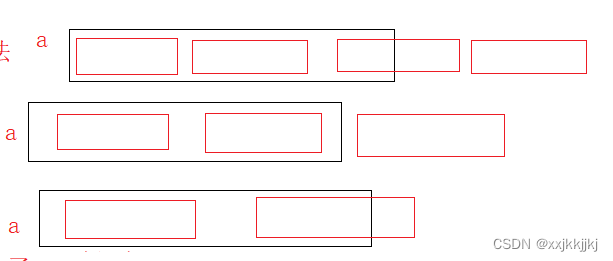

begin1 = i i < n 所以 begin1 一定不会越界
end1 都越界了 begin2 end2肯定也越界了,两个区间没法归并了,就不归了
end1没越界,begin2越界,end2也肯定越界,也没法归并了
end1,begin2没有越界,但是end2越界了,还能修正一下end2 = n-1,继续归并
其实第三步挺重要的。
不参与归并是如何有序的呢?
虽然不参与归并,但是最后平分归并时经过修正后区间begin2没越界 end2 = n-1 也没越界
参与归并数据只不过是少了也就是递归最后[b1 e1] [b2 e2] n/2 n/2 最后一次归并平分成2个有序数组进行归并
不管有几个这种二分越界不参与归并的区间,他们最后一定有中点,那么e1 b2不会越界,e2越界就修正完成非递归的最终归并排序
这个图可以感受最后一次归并数据达不到16个 左边[0,7][8,8]右边修正end2 = n -1 同样也归并排序完成
并且gap<=n/2 也就是gap不会超过半数数据,举例N=8来说,最后是4 4 归并,一组数据个数gap=4,所以他们一定有中点,并且达到平分那么e1 b2肯定不会越界
临时数组拷贝到原数组不能归并后一把梭哈
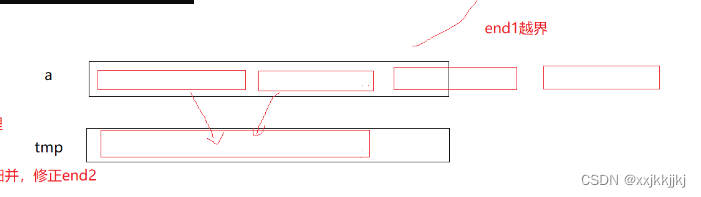
因为你在归并后,可以归并的2段区间没问题,不归并的区间如果没拷贝到tmp中,你又要一把梭哈拷贝回原数组,那么就会导致随机值,所以就得不归并的也得拷贝到tmp中再考回原数组。
不如归并一部分拷贝一部分
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
//int j = 0;
for (int i = 0; i < n; i += (2 * gap))
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//[begin1 end1] [begin2 end2]
//printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
if (end1 >= n || begin2 >= n)//if (begin2 >= n )
{
break;
}
if (end2 >= n )
{
end2 = n - 1;
}
printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])//改稳定 <= 相同数保持前后关系
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
// 归并一部分拷贝一部分
memcpy(a+i, tmp+i, sizeof(int) * (end2-i+1));//不能end2-begin1+1 因为begin1++ 一直在变
}
printf("\n");
gap *= 2;
}
free(tmp);
}
最重要的是区间下标的规律
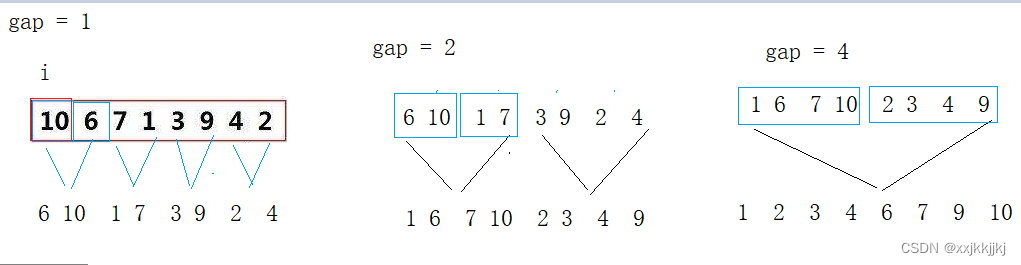
int gap = 1;
while (gap < n)
{
//int j = 0;
for (int i = 0; i < n; i += (2 * gap))
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//[begin1 end1] [begin2 end2]
//printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);
begin1 = i 就带进去看 i += (2 * gap) 跳过这两个组 到下两个组
再看 begin2 = i + gap 跳到下一个区间开始
end1 = i + gap - 1就是begin2 -1
end2 = i + 2 * gap - 1 是begin2 + gap - 1 看规律看出来的
这块结合图中gap =2 和gap=1来看规律
总的来说就是控制好这个下标,并且不要一把梭哈
计数排序
总结:计数排序适合范围集中,且范围不大的整形数组排序。不适合范围分散或者非整形的排序,如:字符串、浮点数等
-
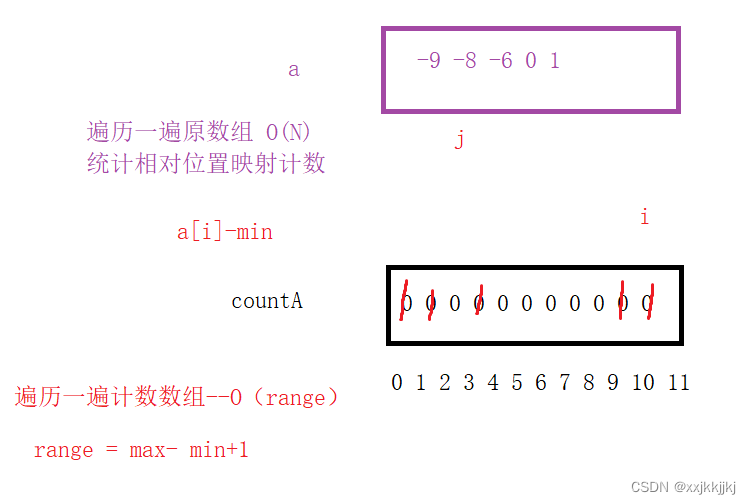
绝对映射

如果范围很大 100~200 如果使用绝对映射,前面的空间全部浪费,所以需要相对映射 -
相对映射

需要注意的是,相对映射 是用a[ i ]-min 来确定映射计数的,并且可以处理负数的排序,但如果范围过大,那么计数排序不再适合。
range = max-min+1是countA空间大小
countA数组一开始都初始化为0
处理负数
完整代码
如果range和N相近就很快
时间复杂度 O(N+range)
空间复杂度 O(range)
多遍历了一次找最大最小 但是常数次N根据时间复杂度规则认为是N
// 计数排序 相对映射可处理负数
//时间复杂度 O(N+range)
//空间复杂度 O(range)
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
int range = max - min + 1;
int* countA = (int*)calloc(range, sizeof(int));
if (countA == NULL)
{
perror("calloc fail");
return;
}
for (int i = 0; i < n; i++)
{
countA[a[i] - min]++;
}
int j = 0;
for (int i = 0; i < range; i++)
{
while (countA[i]--)
{
a[j++] = i + min;
}
}
free(countA);
}