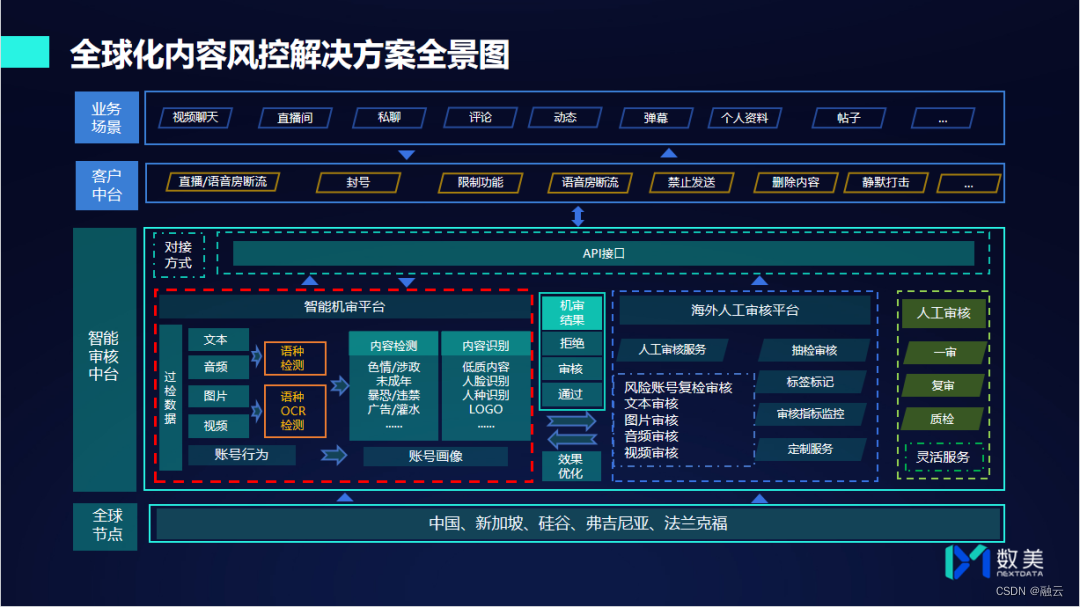
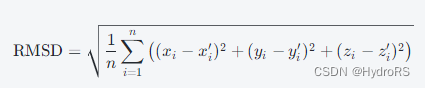题目描述

上面是我们曾经练习过的一个习题，请在原来代码的基础上作以下修改：1、增加自写的析构函数；2、将getDisTo方法的参数修改为getDisTo(const Point &p)；3、根据下面输出的内容修改相应的构造函数。

然后在主函数中根据用户输入的数目建立Point数组，求出数组内距离最大的两个点之间的距离值。

输入

测试数据的组数 t

第一组点的个数

第一个点的 x 坐标   y坐标

第二个点的 x坐标  y坐标

............

输出

输出第一组距离最大的两个点以及其距离（存在多个距离都是最大值的情况下，输出下标排序最前的点组合。比如如果p[0]和p[9]、p[4]和p[5]之间的距离都是最大值，那么前一个是答案，因为p[0]排序最前）

...........

在C++中，输出指定精度的参考代码如下：

#include <iostream>

#include <iomanip> //必须包含这个头文件

using namespace std;

void main( )

{ double a =3.141596;

  cout<<fixed<<setprecision(3)<<a<<endl;  //输出小数点后3位

---

输入样例

2
4
0 0
5 0
5 5
2 10
3
-1 -8
0 9
5 0
 

---

输出样例

Constructor.
Constructor.
Constructor.
Constructor.
The longeset distance is 10.44,between p[1] and p[3].
Distructor.
Distructor.
Distructor.
Distructor.
Constructor.
Constructor.
Constructor.
The longeset distance is 17.03,between p[0] and p[1].
Distructor.
Distructor.
Distructor.
 

---

#include <iomanip>
#include <iostream>
#include <math.h>
using namespace std;
class Point
{
private:
    double x, y;
public:
    Point() {}
   
    //将xy存入对象point里面 并输出"Constructor." 
    void setXY(double x1, double y1) { x = x1, y = y1; cout << "Constructor." << endl; }
    
    //求两点距离
    double getDisTo(const Point& p);

    ~Point()
    {
        cout << "Distructor.\n";
    }
};

//求两点距离
double Point::getDisTo(const Point& p)
{
    double d;
    d = sqrt((x - p.x) * (x - p.x) + (y - p.y) * (y - p.y));
    return d;
}
int main()
{
    int t;
    int  n, i = 0; double x, y;
    cin >> t;
    while (t--)
    {
        cin >> n;//一组n个点
        Point* p = new Point[n];//创建一个动态数组（类） 但是是类

        for (int i = 0; i < n; i++)
        {
            cin >> x >> y;
            p[i].setXY(x, y);//给每个类赋值xy
        }
        double max = 0; 
        int maxindex = 0, minindex = 0;
        for (int i = 0; i < n - 1; i++)
        {
            for (int j = i + 1; j < n; j++)
            {
                if (max < p[i].getDisTo(p[j]))  //求最长距离
                {
                    max = p[i].getDisTo(p[j]);
                    maxindex = i; minindex = j;//获取下标
                }
            }
        } 
        //0-1 0-2 0-3 .....0-(n-1)
        //1-2 1-3 ...1-(n-1)
        //......
        //(n-2)-(n-1)
        
        // fixed << setprecision(2) 保留两位小数
        cout << fixed << setprecision(2) << "The longeset distance is " << max
            << ",between p[" << maxindex << "] and p[" << minindex << "].\n";
        delete[]p;//删除动态数组 
    }
    return 0;
}