文章目录
- 聚合统计(set->共同好友)
- 排序统计(zset->评论排序)
- 二值统计(bitmap->签到打卡)
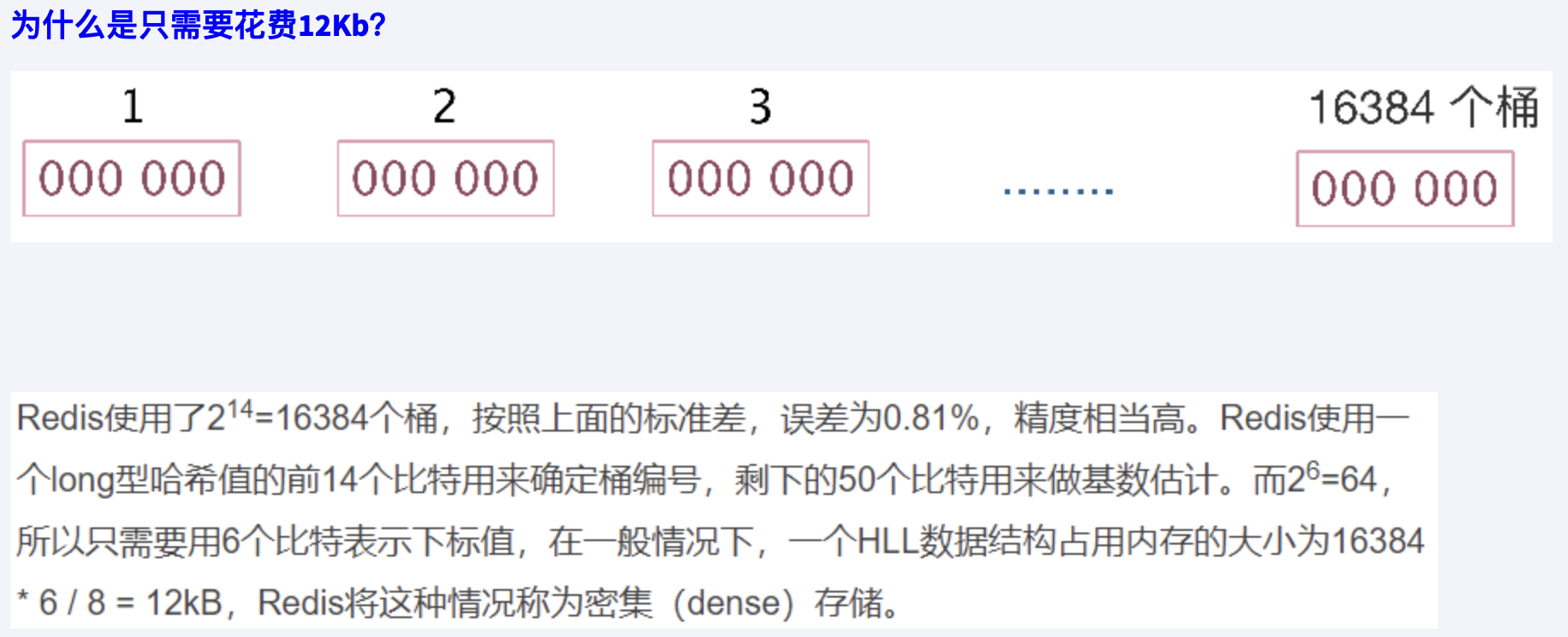
- 基数统计(hyperloglog->亿级UV统计方案)
- 地理坐标(GEO)
- 布隆过滤器
- 面试题
- 定义
- 产生背景
- 作用
- 底层原理
聚合统计(set->共同好友)
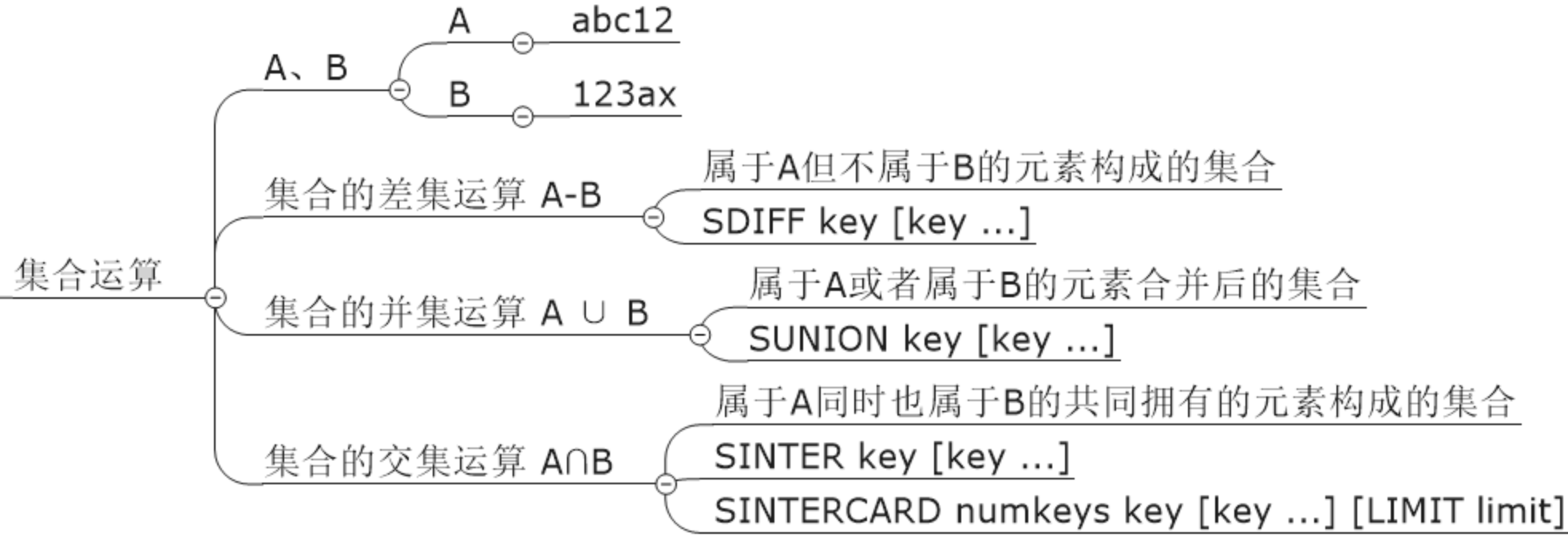
统计多个集合元素的聚合结果,就是前面讲解过的交差并等集合统计
-
集合应用的命令
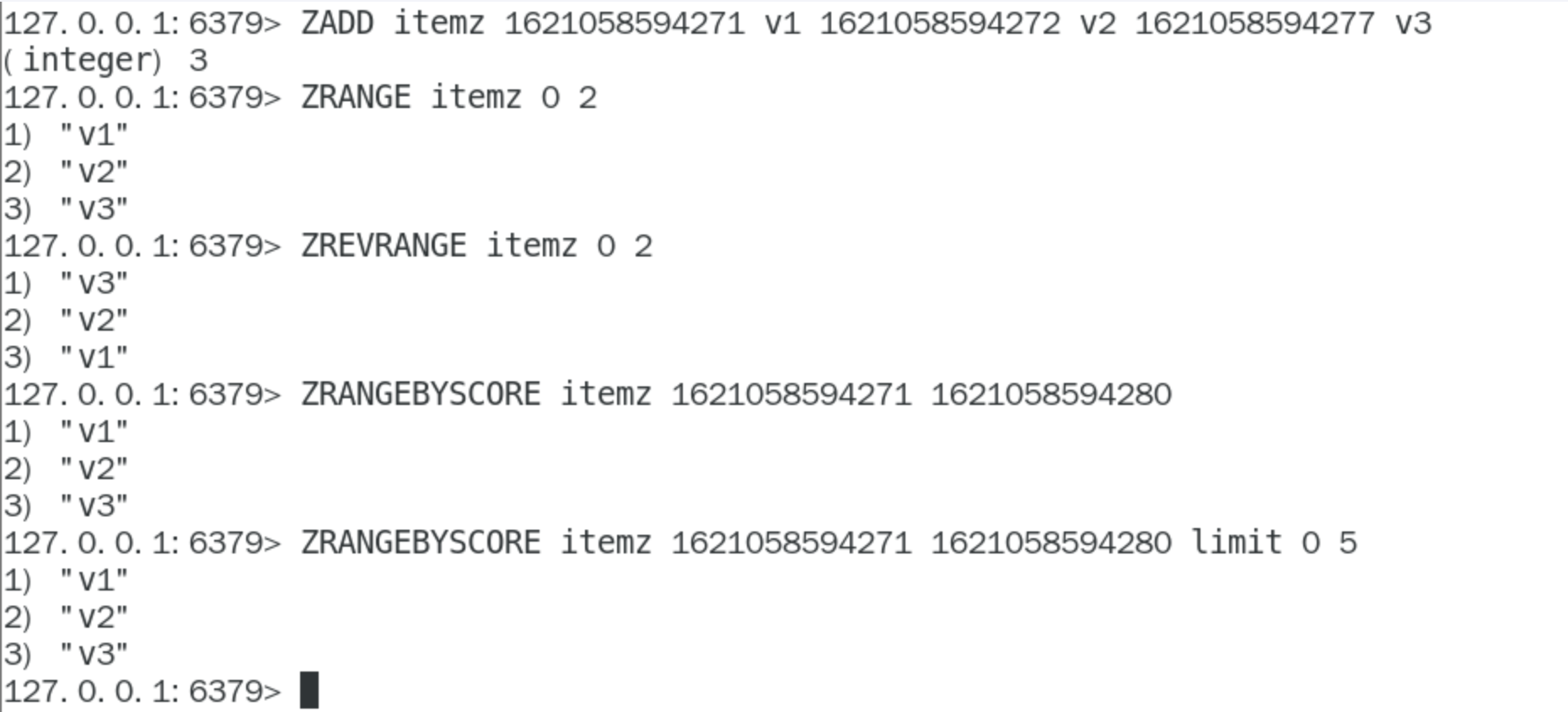
排序统计(zset->评论排序)
抖音短视频最新评论留言的场景,请你设计一个展现列表
考察你的数据结构和设计思路
- 在面对需要展示最新列表、排行榜等场景时如果数据更新频繁或者需要分页显示,建议使用ZSet
二值统计(bitmap->签到打卡)
集合元素的取值就只有0和1两种
-
案例
- 日活统计
- 连续签到打卡
- 最近一周的活跃用户
- 统计指定用户一年之中的登陆天数
- 某用户按照一年365天,哪几天登陆过?哪几天没有登陆?全年中登录的天数共计多少?
-
bitmap数据类型
详情见:https://blog.csdn.net/al6nlee/article/details/129822586
- 即0和1状态表现的二进制位的bit数组
-
京东签到领取京豆
一个Byte一个字节 4个byte正好32位,一个月最多31天,sonice

基数统计(hyperloglog->亿级UV统计方案)
统计一个集合中不重复的元素个数
-
行业名词
- UV
- Unique Visitor,独立访客,一般理解为客户端IP
- 需要去重考虑
- PV
- Page View,页面浏览量
- 不用去重
- DAU(Daily Active User)
- 日活跃用户量->登录或者使用了某个产品的用户数(去重复登录的用户)
- 常用于反映网站、互联网应用或者网络游戏的运营情况
- MAU
- 月活跃用户量
- UV
-
hyperloglog数据类型
详情见:https://blog.csdn.net/al6nlee/article/details/129822586
- 一句话:hyperloglog就是一个集合中不重复的元素的个数,脱水后的真实数据
-
hyperloglog原理
-
引入
统计亿级数据的统计
遍历->bitmap
- 如果要统计1亿个数据的基数位值,大约需要内存100000000/8/1024/1024约等于12M,内存减少占用的效果显著。
- 这样得到统计一个对象样本的基数值需要12M。
- 如果统计10000个对象样本(1w个亿级),就需要117.1875G将近120G,可见使用bitmaps还是不适用大数据量下(亿级)的基数计数场景
- bitmaps方法是精确计算的
bitmap->HyperLogLog
- 对于不要求绝对准确率的场景下可以使用,因为概率算法不直接存储数据本身,通过一定的概率统计方法预估基数值,同时保证误差在一定范围内,由于又不储存数据故此可以大大节约内存。
- HyperLogLog就是一种概率算法的实现
-
定义
只是进行不重复的基数统计,不是集合也不保存数据,只记录数量而不是具体内容
- Hyperloglog提供不精确的去重计数方案
- 牺牲准确率来换取空间,误差仅仅只是0.81%左右
-
-
淘宝网站首页亿级UV的Redis统计方案
-
需求
- UV的统计需要去重,一个用户一天内的多次访问只能算作一次
- 淘宝、天猫首页的UV,平均每天是1~1.5个亿左右
- 每天存1.5个亿的IP,访问者来了后先去查是否存在,不存在加入
-
方案讨论
-
mysql直接忽略
-
redis的hash数据类型->造成bigkey
<keyDay,<ip,1>>
- 按照ipv4的结构来说明,每个ipv4的地址最多是15个字节(ip=“192.168.111.1”,最多xxx.xxx.xxx.xxx)
- 某一天的1.5亿 * 15个字节= 2G,一个月60G
-
hyperloglog
存储原理
-
-
地理坐标(GEO)
-
经纬度
国际上规定,把通过英国格林尼治天文台原址的经线叫做0°所以经线也叫本初子午线。在地球上经线指示南北方向,纬线指示东西方向。
东西半球分界线:东经160° 西经20°
- 经度(longitude):东经为正数,西经为负数。东西经
- 纬度(latitude):北纬为正数,南纬为负数。南北纬
-
获取某个地址的经纬度
百度api:https://api.map.baidu.com/lbsapi/getpoint/
-
GEO数据类型
详情见:https://blog.csdn.net/al6nlee/article/details/129822586
-
美团地图位置附近的酒店推送
需求
布隆过滤器
面试题
- 现有50亿个电话号码,现有10万个电话号码如何要快速准确的判断这些电话号码是否已经存在?
- 判断是否存在,布隆过滤器了解过吗?
- 安全连接网址,全球数10亿的网址判断
- 黑名单校验,识别垃圾邮件
- 白名单校验,识别出合法用户进行后续处理
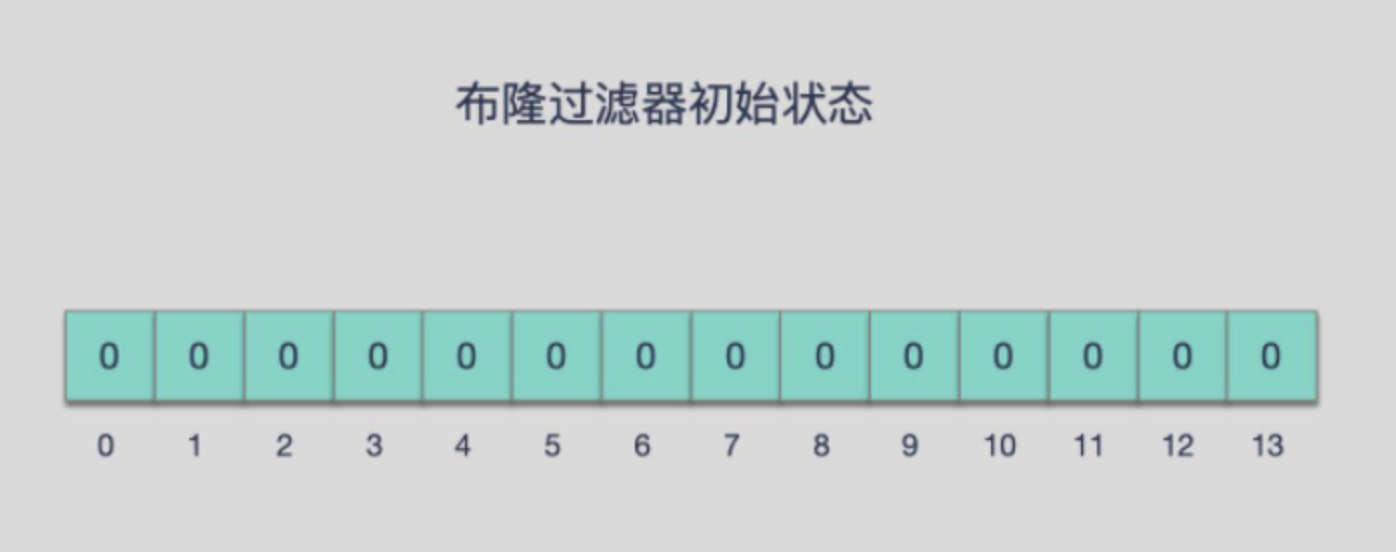
定义
由一个初值都为零的bit数组和多个哈希函数构成,用来快速判断集合中是否存在某个元素
- 快速检索出来具体数据是否存在于一个大的集合中
| 目的 | 减少内存占用 |
|---|---|
| 方式 | 不保存数据信息,只是在内存中做一个是否存在的标记flag |
产生背景
布隆过滤器(英语:Bloom Filter)是 1970 年由布隆提出的。
它实际上是一个很长的二进制数组(00000000…)+一系列随机hash算法映射函数,主要用于判断一个元素是否在集合中。
通常我们会遇到很多要判断一个元素是否在某个集合中的业务场景,一般想到的是将集合中所有元素保存起来,然后通过比较确定。
链表、树、哈希表等等数据结构都是这种思路。但是随着集合中元素的增加,我们需要的存储空间也会呈现线性增长,最终达到瓶颈。同时检索速度也越来越慢,上述三种结构的检索时间复杂度分别为O(n),O(logn),O(1)。这个时候,布隆过滤器(Bloom Filter)就应运而生
作用
-
高效地插入和查询,占用空间少,返回的结果是不确定性+不够完美
目的 减少内存占用 方式 不保存数据信息,只是在内存中做一个是否存在的标记flag -
重点
- 一个元素如果判断结果:存在时,元素不一定存在
- 但是判断结果为不存在时,则一定不存在
-
布隆过滤器可以添加元素,但是不能删除元素->由于涉及hashcode判断依据,删掉元素会导致误判率增加。
底层原理
布隆过滤器(Bloom Filter) 是一种专门用来解决去重问题的高级数据结构。
实质就是一个大型位数组和几个不同的无偏hash函数(无偏表示分布均匀)。由一个初值都为零的bit数组和多个个哈希函数构成,用来快速判断某个数据是否存在。但是跟 HyperLogLog 一样,它也一样有那么一点点不精确,也存在一定的误判概率
-
添加key
使用多个hash函数对key进行hash运算得到一个整数索引值,对位数组长度进行取模运算得到一个位置,
每个hash函数都会得到一个不同的位置,将这几个位置都置1就完成了add操作。
-
查询key
只要有其中一位是零就表示这个key不存在,但如果都是1,则不一定存在对应的key。
**结论:**有,是可能有 无,是肯定无