典型情况下SOC要对设计中各种组件提供许多与相位相关的时钟。将主时钟以2为幂次进行分割来产生同步偶数分频时钟，有时也会需要按奇数或小数进行分频。

同步整数分频器

如下图所示，可以使用Moore状态机很容易地实现同步整数分频，但是这样简单的逻辑无法产生50%占空比的输出。

具有50%占空比的奇数整数分频

在概念上，产生具有50%占空比的奇数分频时钟最简单的方式是以期望输出频率的一半生成两个正交相位时钟（两个时钟之间有90度相位差）。然后通过将两个波形异或得到输出频率。由于存在固定的90度相位差，每次异或输入只有一端会变化，这样有效消除了输出波形上的毛刺。

以下是一个三分频的简单例子：
1）创建由时钟上升沿触发的0到（N - 1）的计数器，N是自然数，用于对参数时钟进行分频（N不等于偶数）
对三分频，从0计数到2，N=3；对五分频，从0计数到4，N=5；对七分频，从0计数到6，N=7。
计数器在输入时钟（ref_clk）上升沿累加，在到达（N - 1）后自动归零。
2）使用两个开关触发器，按以下方式产生其使能信号。
tff1_en：TFF1在计数值为0时使能。
tff2_en：TFF2在计数值为（N+1）/ 2时使能（2对应三分频，3对应五分频，依此类推），如下图所示。

3）产生以下信号：
div1：TFF1的输出（由输入时钟ref_clk上升沿触发）。
div2：TFF2的输出（由输入时钟ref_clk下降沿触发）。
4）通过异或div1和div2波形，产生最终输出时钟clkout。

该三分频电路的逻辑结构图如下：

非整数分频（非50%占空比）

• 具有非50%占空比的1.5倍分频

1.5分频的意义即每三个参考时钟包含两个对称的脉冲。
下图中的多路器在clkout为高时选择ref_clk，否则它选择反向后的ref_clk。

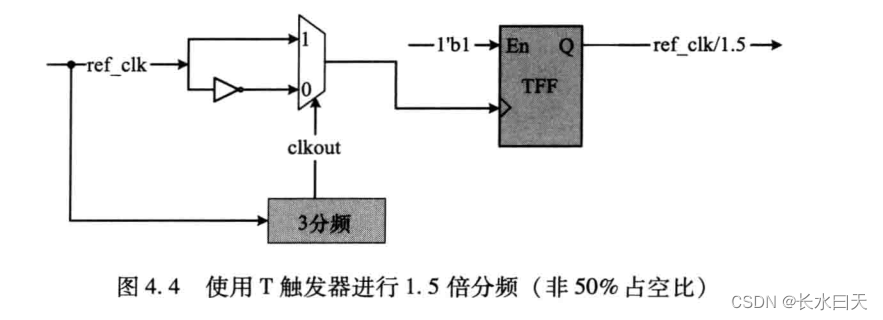
时序图如下：

要注意的是，上述电路在仿真时可以正常工作，但是在综合时可能出现问题，因为在多路器的选择端切换开关时两个输入端的延时并不相等。多路器的输出不能马上改变并可能在输出时钟上产生毛刺。随着参考时钟ref_clk频率的增加，出现错误的可能性会越来越大。

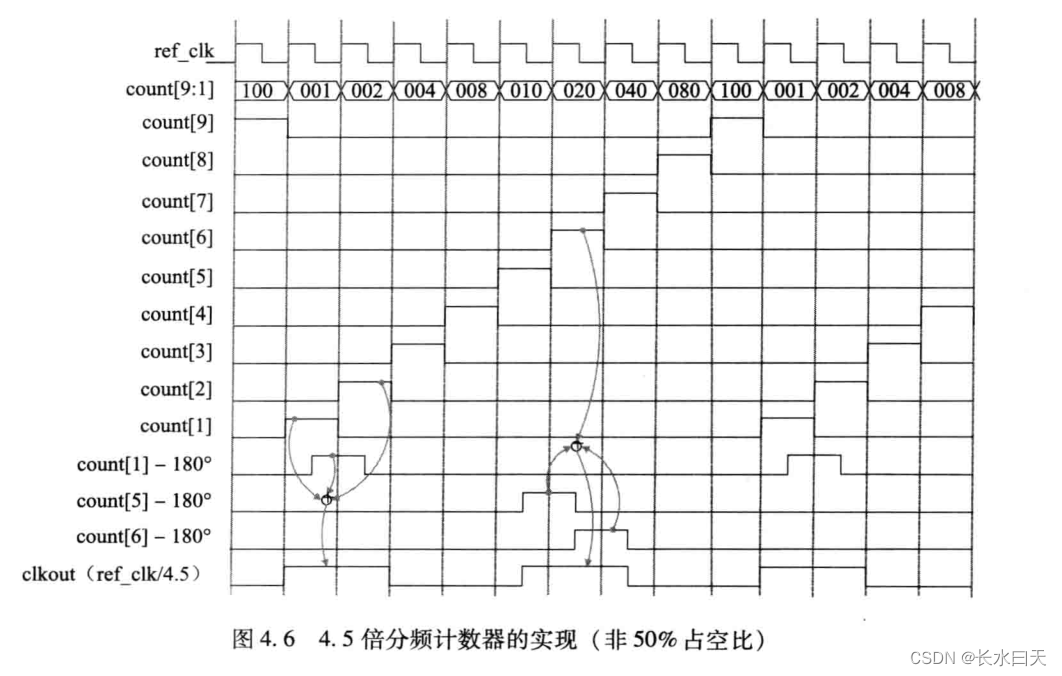
• 具有非50%占空比的4.5倍分频计数器的实现

本节的方法可以通过移位的方法对非整数分频电路进行优化，使其输出时钟完全不含毛刺。

下面是4.5倍分频的例子，即每9个参考时钟包含2个对称脉冲。
1）使用复位值为000000001的9位移位寄存器，可以在每一个时钟上升沿使移位寄存器循环左移一位。
2）要产生第一个脉冲，必须使在半周期时移动第1位并将第1位与第2位进行或操作。
3）要产生第二个脉冲，第5位和第6位必须在半周期时移动并与原始第6位进行或操作。（所有的这些移位操作都是用来保证输出波形不含毛刺的必要操作）

经过上述操作产生的时钟占空比为40%，并且输出不含毛刺。
时序图如下：

Verilog代码如下：