案例问题:假设有两个序列:ATGCG 和 ACCG,如何求得它们的最佳匹配方案。
1. Needleman-Wunsch 算法
原理是动态规划,是一个全局比对算法
算法求解步骤:
(1)在它们前面各加上一个 ‘-’
-ATGCG
-ACCG
(2)设置得分规则(这里分数可手动设定)
match = 1:匹配得一分mismatch = -1:不匹配扣一分indel = -2:插入或缺失对于匹配度的影响会比 mismatch 更严重一点,所以罚分要更多一点
(3)计算得分矩阵
动态规划的状态转移方程:
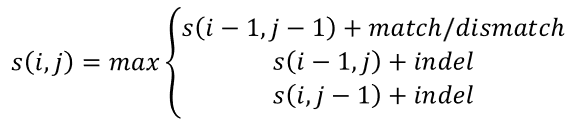

(4)回溯:从得分矩阵的右下角开始,根据每个元素的来源向左上角回溯(这里规定,当一个元素有两个或三个相同的来源时,优先选择来源处得分高的路径)

根据回溯的路径可得最佳匹配方案为:
ATGCG
AC-CG
2. Smith-Waterman 算法
原理是动态规划,是一个局部比对算法
算法求解步骤:
(1)在它们前面各加上一个 ‘-’
-ATGCG
-ACCG
(2)设置得分规则(这里分数可手动设定)
match = 1:匹配得一分mismatch = -1:不匹配扣一分indel = -2:插入或缺失对于匹配度的影响会比 mismatch 更严重一点,所以罚分要更多一点
(3)计算得分矩阵
动态规划的状态转移方程:

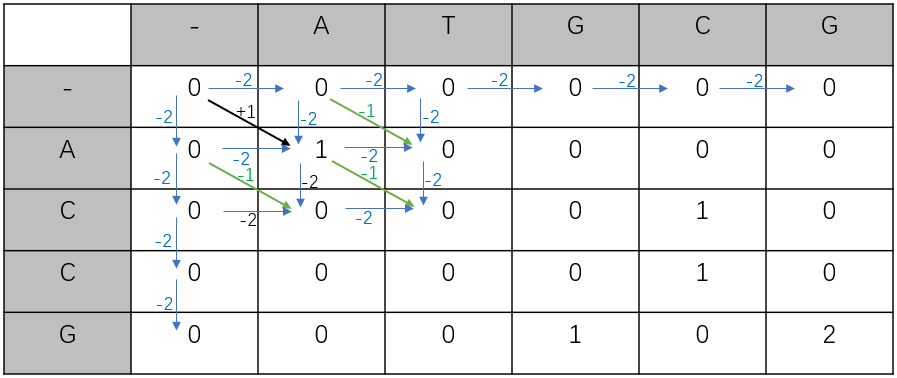
(4)回溯:从得分矩阵的最大值开始,根据每个元素的来源向左上角回溯,碰到 0 就停止回溯。

根据回溯的路径可得最佳匹配方案为:
CG
CG
3. BLOSUM 得分矩阵
BLOSUM:一个用于蛋白质序列排列的替换矩阵,以局部比对为基础对不同的蛋白质序列进行评分。在BLOCKS数据库中,寻找蛋白质序列排列中非常相近的区域,然后计算氨基酸的相对频率和它们的替换概率,并为20个标准氨基酸的210个可能的替换对中的每一个计算出对数得分。
例子:给定如下 6 个序列,计算其 BLOSUM 得分矩阵
计算步骤: