leetcode654 最大二叉树
654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
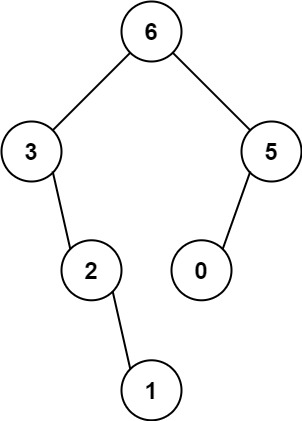
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。 - [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。 - 空数组,无子节点。 - [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。 - 空数组,无子节点。 - 只有一个元素,所以子节点是一个值为 1 的节点。 - [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。 - 只有一个元素,所以子节点是一个值为 0 的节点。 - 空数组,无子节点。示例 2:
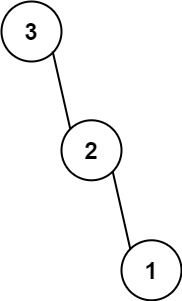
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
代码
// leetcode654.最大二叉树
// 回溯
class Solution {
public:
TreeNode* bulidTree(vector<int> nums)
{
int size = nums.size();
if (size == 0)
{
return nullptr;
}
if (size == 1)
{
TreeNode* cur = new TreeNode(nums[0]);
return cur;
}
int max_num = INT_MIN;
int max_index = -1;
for (int i = 0; i < size; ++i)
{
if (nums[i] > max_num)
{
max_num = nums[i];
max_index = i;
}
}
TreeNode* cur = new TreeNode(max_num);
vector<int>leftnums(nums.begin(), nums.begin() + max_index);
vector<int>rightnums(nums.begin() + max_index + 1, nums.end());
cur->left = bulidTree(leftnums);
cur->right = bulidTree(rightnums);
return cur;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return bulidTree(nums);
}
};leetcode617 合并二叉树
617. 合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
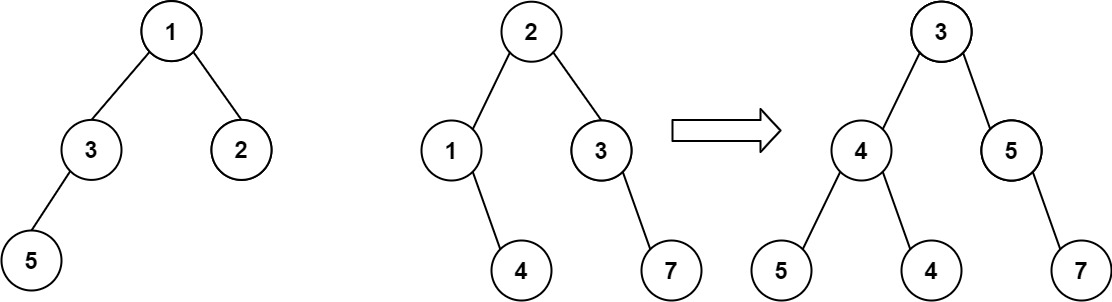
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出:[3,4,5,5,4,null,7]示例 2:
输入:root1 = [1], root2 = [1,2] 输出:[2,2]
代码
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr)
{
return root2;
}
if (root2 == nullptr)
{
return root1;
}
TreeNode* root = new TreeNode(root1->val + root2->val);
root->left = mergeTrees(root1->left, root2->left);
root->right = mergeTrees(root1->right, root2->right);
return root;
}
};