快速排序及优化

概要

关于快速排序的原理不赘述，可以查看912. 排序数组 - 力扣（Leetcode）

本篇文章旨在提供快速排序的C#实现，并通过随机pivot，三数取中，小区间使用插入排序，栈实现，合并pivot以缩小分割范围等方式对快速排序进行优化。

要点

快速排序是不稳定排序
快速排序的期望时间复杂度为O(nlog⁡n)，最差为O(n)。
快速排序的期望空间复杂度为O(logn)，最差情况下是O(n)，取决于递归的次数。
快速排序通常是用于排序的最佳使用选择，这是因为它的平均性能较好。虽然最差情况下时间复杂度是O(n^2)。
因此围绕着快速排序的各种优化都是集中于如何让它的时间复杂度达到期望的时间复杂度。

算法步骤

挑选基准值
分割(partition)三块
递归排序子序列

基础版—使用边界作为pivot

简单版，以最左元素为pivot。

这个的思路是i从左往右找，j从右往左找，便于理解但是效率不高。

public class Solution {
    private int PartSort(int[] nums, int l, int r) {
        Console.WriteLine($"part sort, l={l}, right={r}");

        int i = l + 1;
        int j = r;
        int pivot = GetPivot(nums, l);

        while (i <= j) {
            // 找到本轮的i,j位置
            while (i <= j && nums[i] < pivot) {
                i++;
            }
            while (i <= j && nums[j] > pivot) {
                j--;
            }

            // 进行交换
            if (i <= j) {
                (nums[i], nums[j]) = (nums[j], nums[i]);
                i++;
                j--;
            }
        }

        // 将 pivot 放到正确的位置
        (nums[l], nums[j]) = (nums[j], nums[l]);
        return j;
    }


    private int GetPivot(int[] nums,int l){
        return nums[l];
    }
    // 快排
    public void QuickSort(int[] nums,int l,int r){
        if(l<r ){
            // 分治
            int pos = PartSort(nums,l,r);
            // 递归
            QuickSort(nums,l,pos-1);
            QuickSort(nums,pos+1,r);
        }

    }

    public int[] SortArray(int[] nums) {
        QuickSort(nums,0,nums.Length - 1);
        return nums;
    }
}

改进思路-随机pivot

随机pivot是为了减少选到最大最小值的概率。

但随机也会选到不好的pivot，实际上随机数对排序提供的帮助不大。

给出实现方案，在这个实现方案中同时改进了指针遍历的方式，i,j指针都从左往右找。

public class Solution
{
    private Random random = new Random();
    private int Partition(int[] nums, int l, int r)
    {
        // 随机pivot并和最右侧的数交换
        int i = l + random.Next(r - l + 1);
        int pivot = nums[i];
        (nums[r], nums[i]) = (nums[i], nums[r]);
        // 初始化i
        i = l - 1;
        // j指针找小，i指针留在原地不动，等到j指针找到了，i指针再动
        for (int j = l; j < r; j++)
        {
            if (nums[j] < pivot)
            {
                i++;
                (nums[i], nums[j]) = (nums[j], nums[i]);
            }
        }
        (nums[i + 1], nums[r]) = (nums[r], nums[i + 1]);
        return i + 1;
    }



    // 快排
    public void QuickSort(int[] nums, int l, int r)
    {
        if (l < r)
        {
            // 分治
            int pos = Partition(nums, l, r);
            // 递归
            QuickSort(nums, l, pos - 1);
            QuickSort(nums, pos + 1, r);
        }

    }

    public int[] SortArray(int[] nums)
    {
        QuickSort(nums, 0, nums.Length - 1);
        return nums;
    }
}

花头—使用栈实现

上述代码是递归实现的，自然可以改成栈形式。

public class Solution
{
    private Random random = new Random();
    private int Partition(int[] nums, int l, int r)
    {
        // 随机pivot并和最右侧的数交换
        int i = l + random.Next(r - l + 1);
        int pivot = nums[i];
        (nums[r], nums[i]) = (nums[i], nums[r]);
        // 初始化i
        i = l - 1;
        // j指针找小，i指针留在原地不动，等到j指针找到了，i指针再动
        for (int j = l; j < r; j++)
        {
            if (nums[j] < pivot)
            {
                i++;
                (nums[i], nums[j]) = (nums[j], nums[i]);
            }
        }
        (nums[i + 1], nums[r]) = (nums[r], nums[i + 1]);
        return i + 1;
    }



    // 快排
    public void QuickSort(int[] nums, int l, int r)
    {
        Stack<int> stack = new Stack<int>();
        stack.Push(r);
        stack.Push(l);
        
        while(stack.Count > 0){
            l = stack.Pop();
            r = stack.Pop();
            if(l<r){
                int pos = Partition(nums,l,r);
                // 递归改栈
                stack.Push(r);
                stack.Push(pos+1);
                stack.Push(pos-1);
                stack.Push(l);
            }
        }


    }

    public int[] SortArray(int[] nums)
    {
        QuickSort(nums, 0, nums.Length - 1);
        return nums;
    }
}

改进思路—三数取中作pivot

为了让选择的pivot更接近中位数，可以将头中尾三个数字先进行排序，然后用三个数字取中间数。这样可以保证取出来的不是最小的也不是最大的，最起码是第二小/大的。

而且随机数本身也有开销。可以用median-of-three来替代随机数取pivot。

理论上三数取中会更接近于中位数。但LeetCode的测试用例可能比较特殊，我提交后发现运行效率更低了……

public class Solution
{

    private void DealPivot(int[] nums,int l,int r){
        int med =  (r+l)/2;
        if (nums[l] > nums[med]) {
            (nums[l], nums[med]) = (nums[med], nums[l]);
        }
        if (nums[l] > nums[r]) {
            (nums[l], nums[r]) = (nums[r], nums[l]);
        }
        if (nums[med] > nums[r]) {
            (nums[med], nums[r]) = (nums[r], nums[med]);
        }
        (nums[r-1], nums[med]) = (nums[med], nums[r-1]);
    }
    private int Partition(int[] nums, int l, int r)
    {
        // 随机pivot并和最右侧的数交换
        DealPivot(nums,l,r);
        int pivot = nums[r];
        // 初始化i
        int i = l - 1;
        // j指针找小，i指针留在原地不动，等到j指针找到了，i指针再动
        for (int j = l; j < r; j++)
        {
            if (nums[j] < pivot)
            {
                i++;
                (nums[i], nums[j]) = (nums[j], nums[i]);
            }
        }
        (nums[i + 1], nums[r]) = (nums[r], nums[i + 1]);
        return i + 1;
    }



    // 快排
    public void QuickSort(int[] nums, int l, int r)
    {
        if (l < r)
        {
            // 分治
            int pos = Partition(nums, l, r);
            // 递归
            QuickSort(nums, l, pos - 1);
            QuickSort(nums, pos + 1, r);
        }

    }

    public int[] SortArray(int[] nums)
    {
        QuickSort(nums, 0, nums.Length - 1);
        return nums;
    }
}

改进思路—小区间使用插入排序

插入排序在8个左右以下的时候效率非常高。尤其是已部分排序的数组。

实现很简单，就是QuickSort执行递归前，先看看r-l是否小等于8，如果是，不用QuickSort，而用InsertSort

public class Solution
{

  private Random random = new Random();
    private int Partition(int[] nums, int l, int r)
    {
        // 随机pivot并和最右侧的数交换
        int i = l + random.Next(r - l + 1);
        int pivot = nums[i];
        (nums[r], nums[i]) = (nums[i], nums[r]);
        // 初始化i
        i = l - 1;
        // j指针找小，i指针留在原地不动，等到j指针找到了，i指针再动
        for (int j = l; j < r; j++)
        {
            if (nums[j] < pivot)
            {
                i++;
                (nums[i], nums[j]) = (nums[j], nums[i]);
            }
        }
        (nums[i + 1], nums[r]) = (nums[r], nums[i + 1]);
        return i + 1;
    }

    // 插入排序
    private void InsertSort(int[] nums,int l,int r){
        int j;
        int key;
        for(int i=l+1;i<=r;i++){
            key = nums[i];
            j = i-1;
            while(j >= l && key < nums[j]){
                // 后移
                nums[j+1] = nums[j];
                j--;
            }
            nums[j+1] = key;
        }
    }


    // 快排
    public void QuickSort(int[] nums, int l, int r)
    {
        if (l < r)
        {
            if(r-l<=7){
                InsertSort(nums,l,r);
            }
            else{
                // 分治
                int pos = Partition(nums, l, r);
                // 递归
                QuickSort(nums, l, pos - 1);
                QuickSort(nums, pos + 1, r);
            }
        }

    }

    public int[] SortArray(int[] nums)
    {
        QuickSort(nums, 0, nums.Length - 1);
        return nums;
    }
}

改进思路—缩小分割范围，与pivot相同的合并在一起

可以把和pivot相同的数合并到pivot左右的位置，这样分割后两边的范围就会变小，省去了很多不必要的排序。

尤其适用于大量重复的数组。

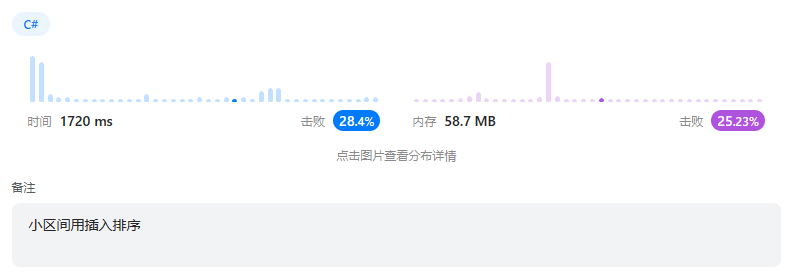
912. 排序数组 - 力扣（Leetcode）加了个五万个2的测试用例……官方用例都要通不过了。

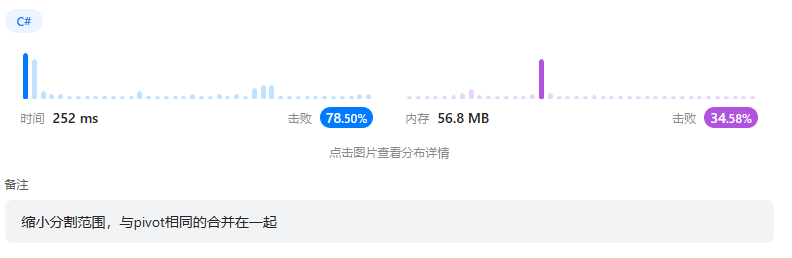
这个思路可以很好地解决这个用例，耗时从1720ms提升到252ms……

改进前：

改进后：

具体来说就是在执行Partition的时候增加两个指针，分别是指向比pivot小的lt和指向比pivot大的rt。

j用来遍历数组。

当nums[j]==pivot的时候，不再需要交换元素。这样经过循环后。

当nums[j]<pivot的时候，交换元素，并且lt左移1。

当nums[j]>pivot的时候，交换元素，并且gt右移1。

l <= lt < j：nums[l...lt]中的元素都小于pivot。
lt < j <= gt：nums[lt+1...j-1]中的元素都等于pivot。
gt < r：nums[gt+1...r-1]中的元素都大于pivot。

QuickSort原本是Sort pos两边的数组，现在只需要Sortlt左边的和rt右边的数组。

完整代码如下：

public class Solution
{
    private Random random = new Random();

    private (int, int) Partition(int[] nums, int l, int r)
    {
        // 随机pivot并和最右侧的数交换
        int i = l + random.Next(r - l + 1);
        int pivot = nums[i];
        (nums[r], nums[i]) = (nums[i], nums[r]);

        // 初始化i, j, k
        int lt = l; // 指向比pivot小的数
        int gt = r - 1; // 指向比pivot大的数
        int j = l;

        while (j <= gt)
        {
            if (nums[j] < pivot)
            {
                (nums[lt], nums[j]) = (nums[j], nums[lt]);
                lt++;
                j++;
            }
            else if (nums[j] > pivot)
            {
                (nums[gt], nums[j]) = (nums[j], nums[gt]);
                gt--;
            }
            else
            {
                j++;
            }
        }

        (nums[gt + 1], nums[r]) = (nums[r], nums[gt + 1]);
        return (lt, gt + 1);
    }

    // 插入排序
    private void InsertSort(int[] nums, int l, int r)
    {
        int j;
        int key;
        for (int i = l + 1; i <= r; i++)
        {
            key = nums[i];
            j = i - 1;
            while (j >= l && key < nums[j])
            {
                // 后移
                nums[j + 1] = nums[j];
                j--;
            }
            nums[j + 1] = key;
        }
    }

    // 快排
    public void QuickSort(int[] nums, int l, int r)
    {
        if (l < r)
        {
            if (r - l <= 7)
            {
                InsertSort(nums, l, r);
            }
            else
            {
                // 分治
                (int pos_l, int pos_r) = Partition(nums, l, r);
                // 递归
                QuickSort(nums, l, pos_l - 1);
                QuickSort(nums, pos_r + 1, r);
            }
        }
    }

    public int[] SortArray(int[] nums)
    {
        QuickSort(nums, 0, nums.Length - 1);
        return nums;
    }
}