目录
一.问题
题目描述
输入格式
输出格式
输出样例
二.解题思路
合法性判定(状态压缩):
推导dp式:
代码实现:
一.问题
题目描述
小明最近迷上了积木画,有这么两种类型的积木,分别为 I 型(大小为 2 个单位面积)和 L 型(大小为 3 个单位面积):
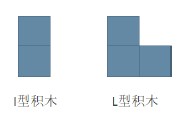
同时,小明有一块面积大小为 2 × N 的画布,画布由 2 × N 个 1 × 1 区域构成。
小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式?
积木可以任意旋转,且画布的方向固定。
输入格式
输入一个整数N,表示画布大小。
对于所有测试用例,1 ≤ N ≤ 10000000。
输出格式
输出一个整数表示答案。由于答案可能很大,所以输出其对 1000000007 取模后的值
3输出样例
5二.解题思路
合法性判定(状态压缩):
由于上一列的摆放会影响当前列,所以我们要对每一列积木的摆放方法进行检查,剔除掉不合法的操作。这样我们就需要判断能否从上一列的状态转换到当前列的状态。由于本题画步的高度是固定的,且值很小,所以我们可以枚举这两列所有的状态。每一列有两个格子,每个格子只会有两种状态,摆放或者不摆放。这里要引入状态压缩,把这一列的两个格子分别当成二进制位,摆放的格子就是1,不摆放就是0,我们让下面的格子是低位,上面的格子是高位。这样就能组合出一个十进制数,就可以用0,1,2,3表示当前列的四种状态(因为每 一列有两个格子,每个格子有两种状态一共就是四种状态)。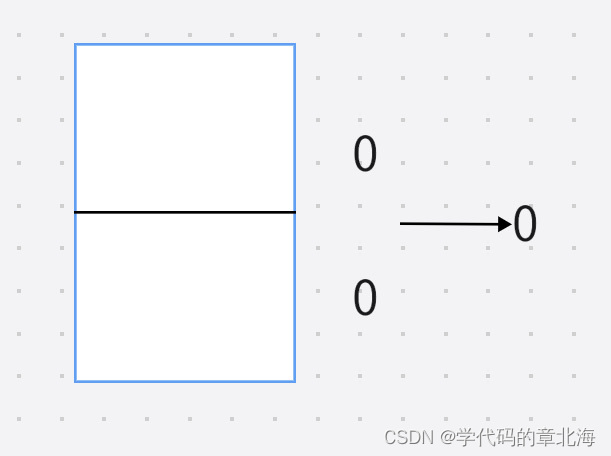
第一种状态,两个格子都不放,十进制为0.
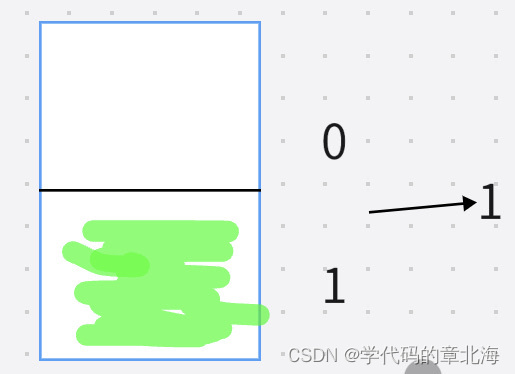
第二种状态,下面格子被占用,十进制为1
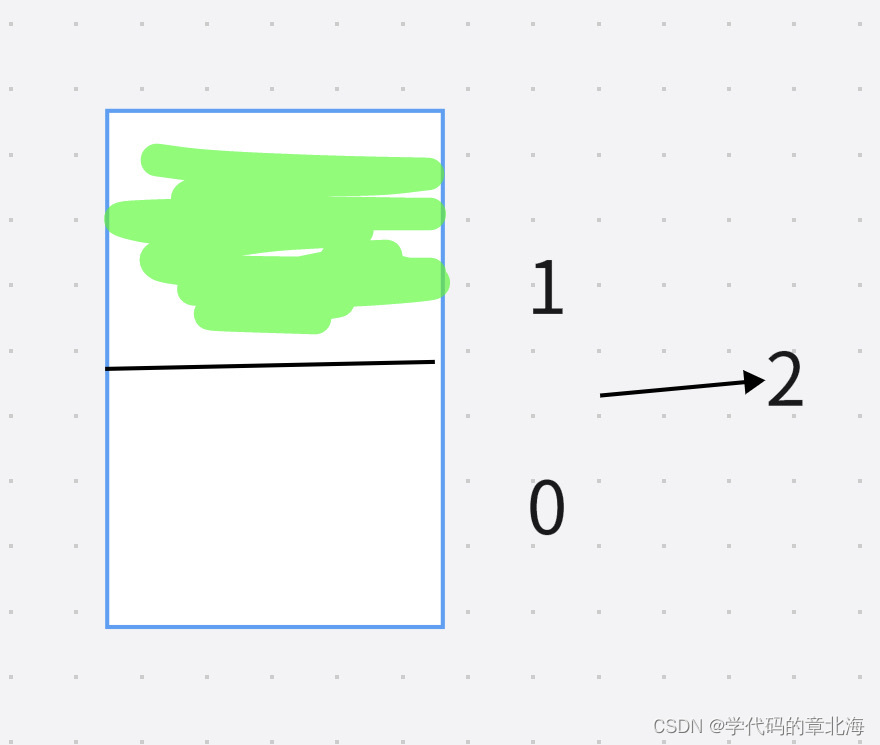
第三种状态,上面格子被占用,十进制为2
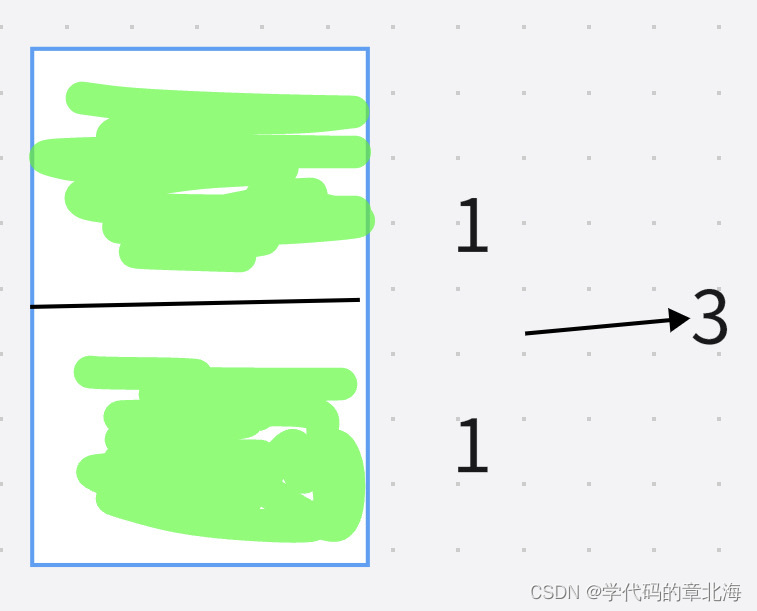
第四种状态,两个格子被占用,十进制为3
对于下一列我们也可以采取这种表达方式。所以下一列的四种状态也可以用0,1,2,3来表示,这样我们就可以通过一个二维数组f[i][j]来判断能否从当前状态转移到下一列的其他状态。我们可以让状态作为数组下表,所以状态到状态的转移就变成了下标到下标的转移。能转移记值为1,不能转移则为0.接下来我们需要判断这16种方案哪些合法。(我们取每块积木最左侧的方块作为操作)
- 当前一列状态数为0,判断后一列状态数能否为0,1,2,3:
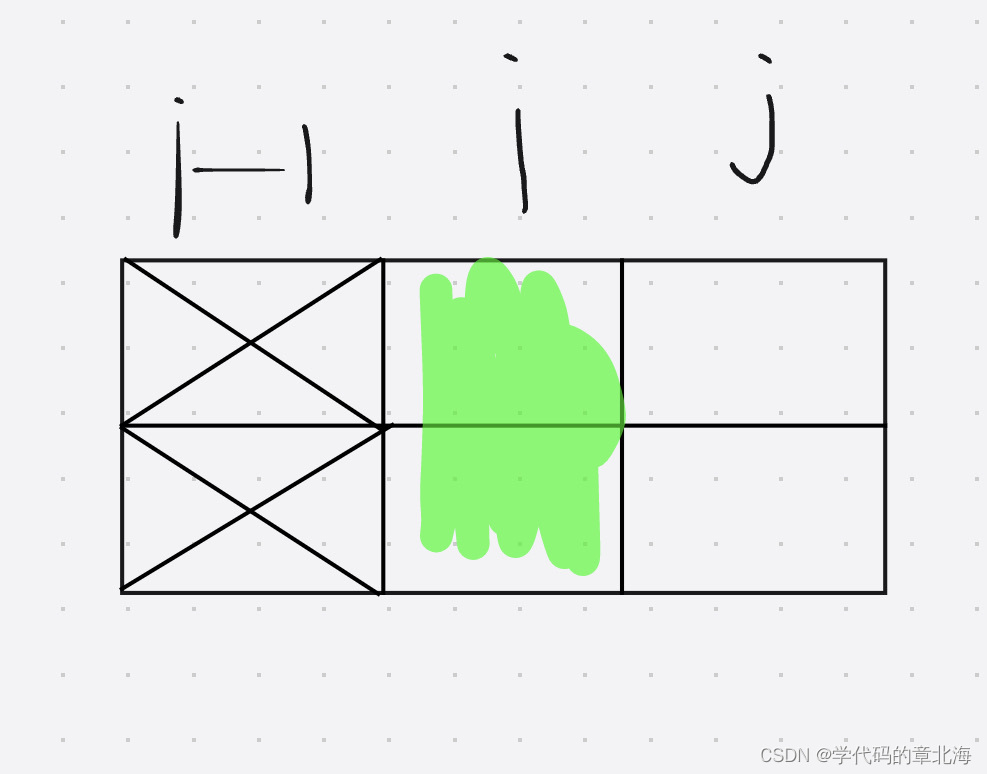
当前列原来状态是0,由于当前列在操作过后必须要填满,否则不符合题意。当前j的状态是0.所以0状态可以转移到0状态。f[0][0] = 1
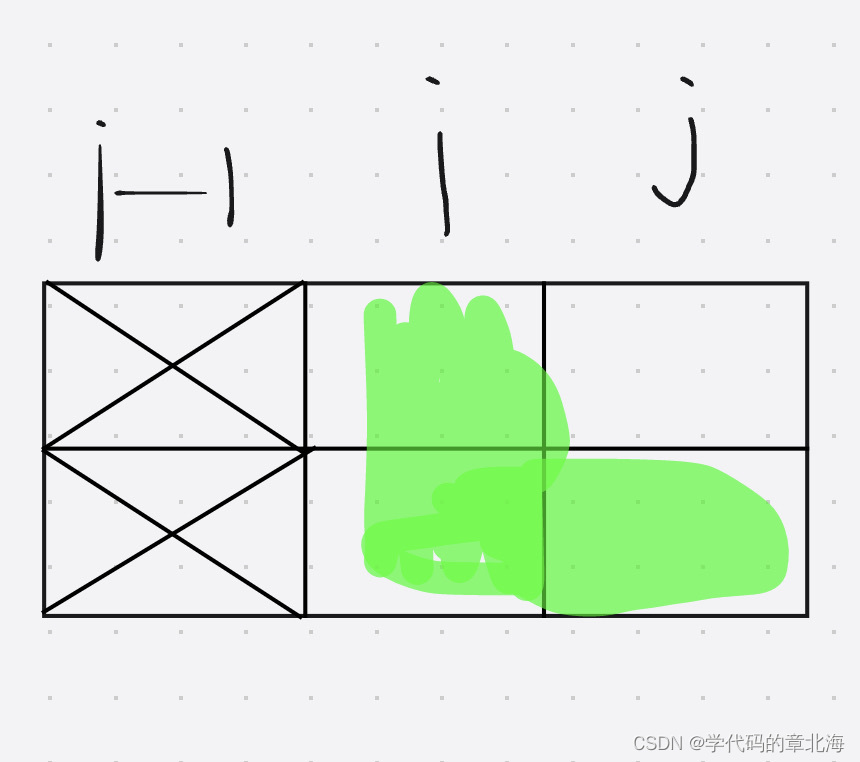
由图片可以得到从0转移到1的状态也是可以的。f[0][1] = 1
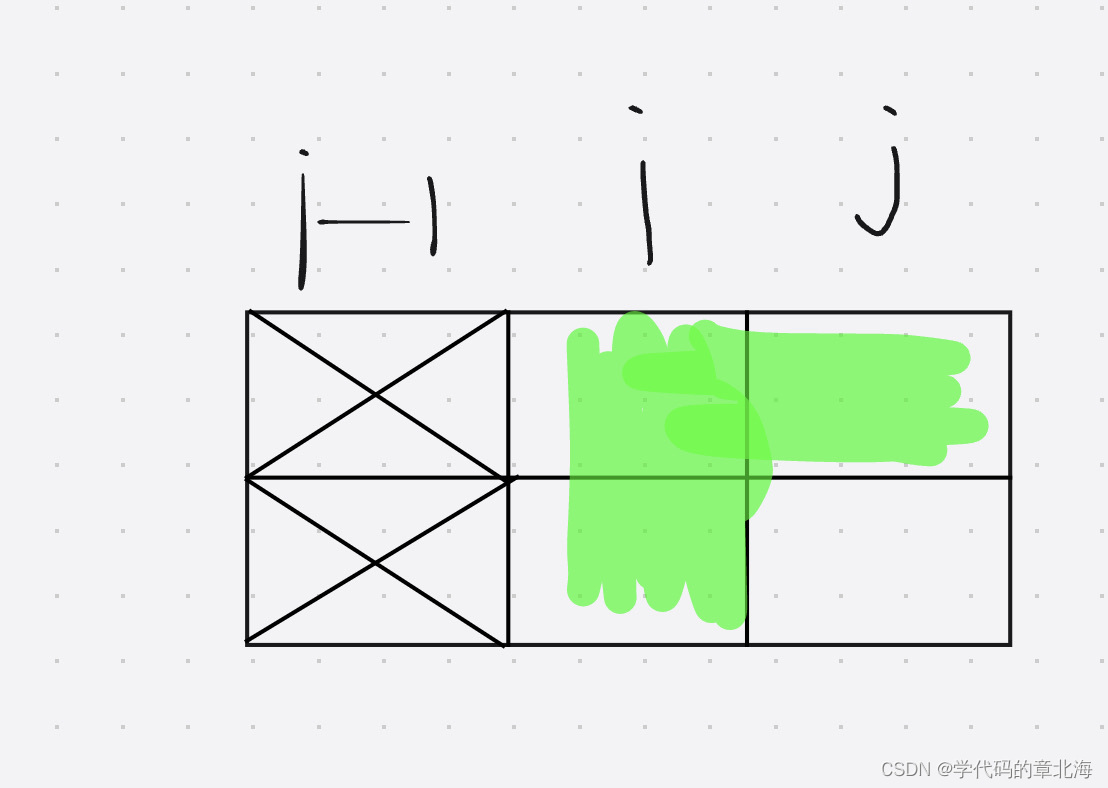
同理f[0][2]=1
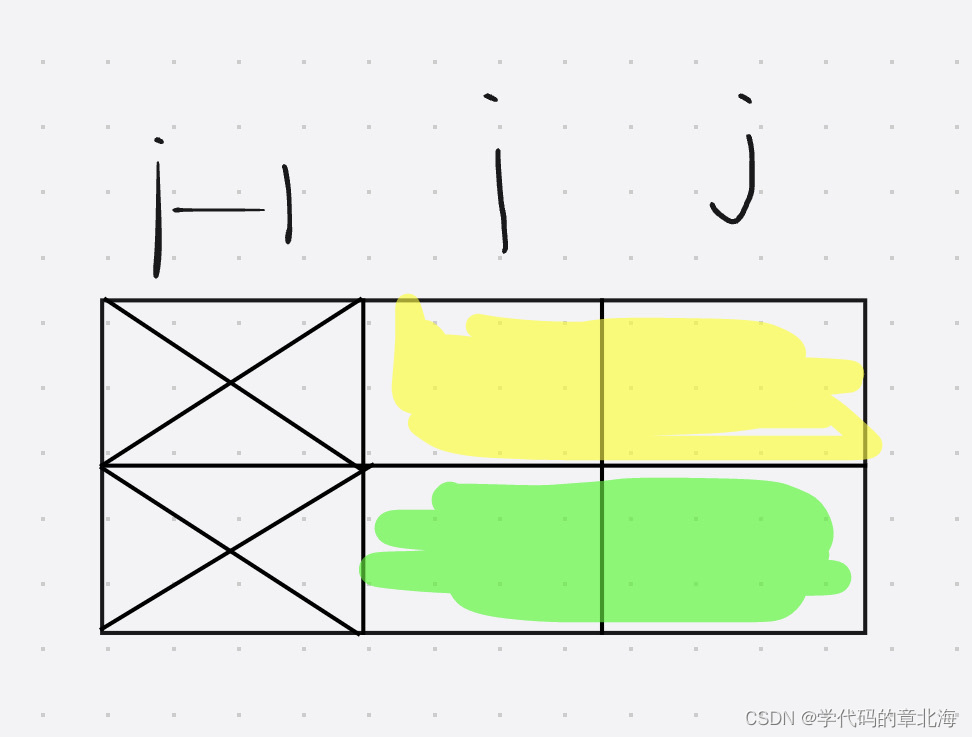
同样j是3的时候也是可以转化成功的
- 当前i状态是1的时候:
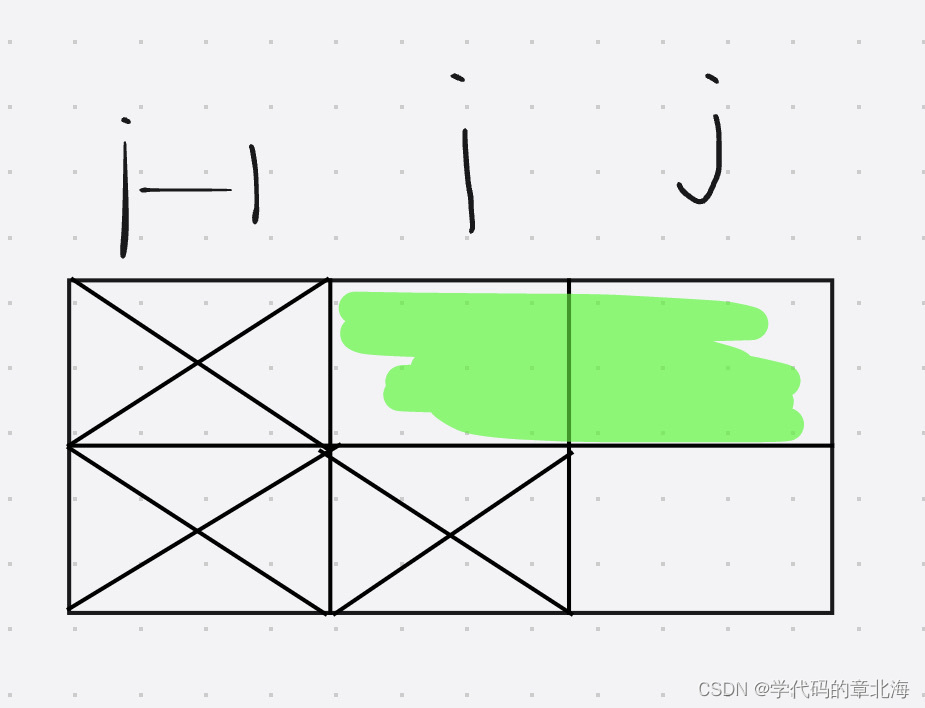
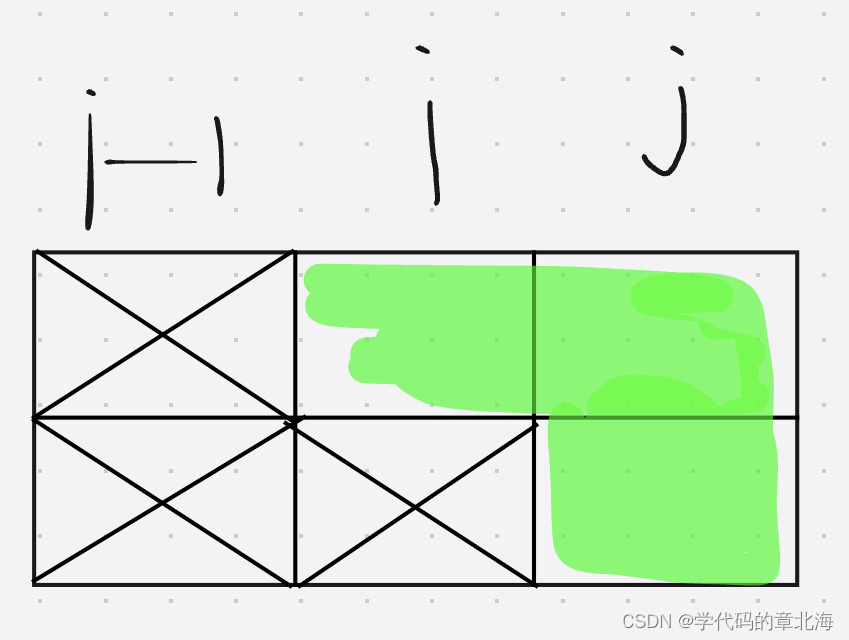
为保证i列操作后必须要填满,只有当j满足上两种状态的时候才能转化,所以f[1][2] = 1,f[1][3] =1
- 当前i状态是2的时候:
其实本质和i是1的情况是一样的,只不过是反转了一下。
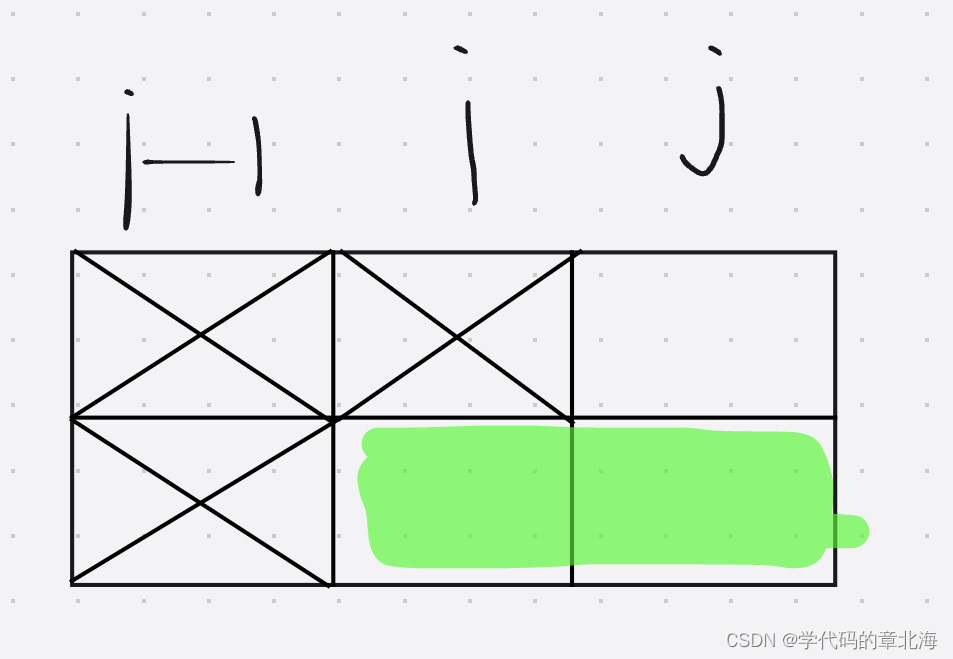
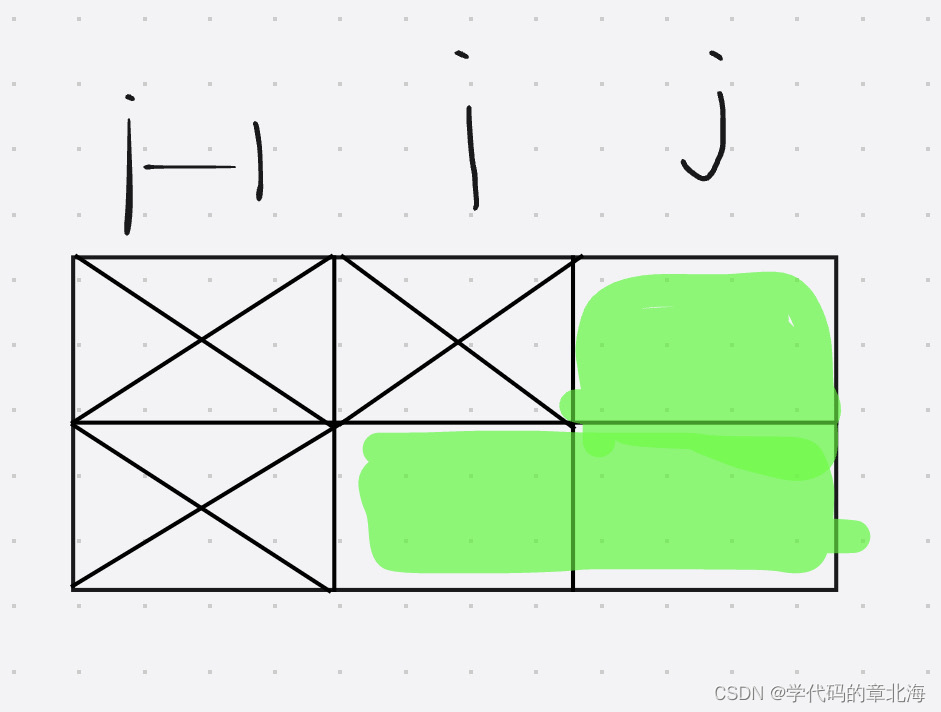
同样可得f[2][3] =1,f[2][1] =1
- 当i的状态是3的时候:
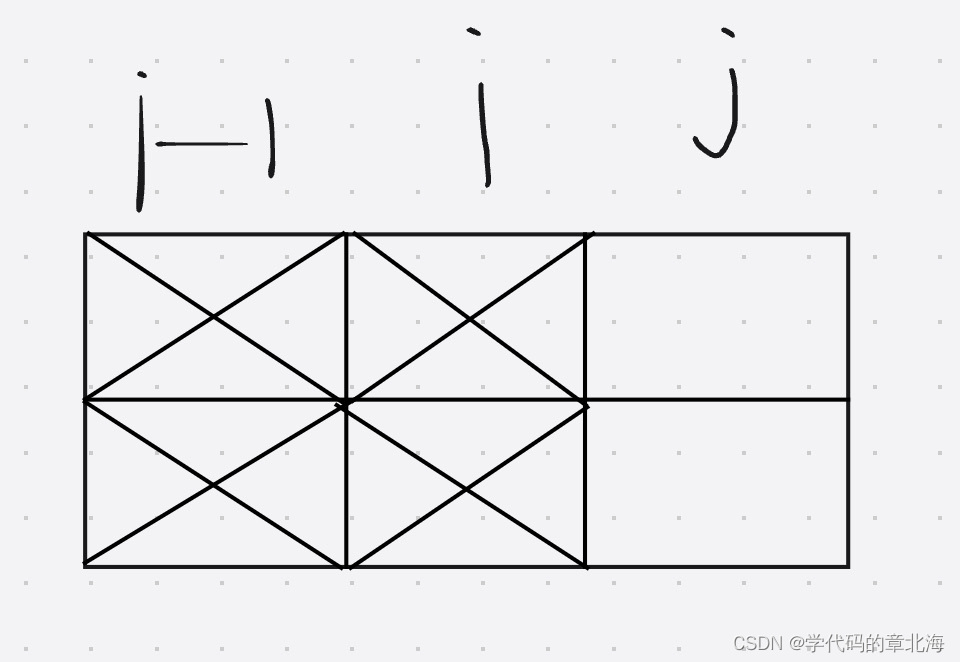
由于此时i已经被上一列填满了,同时我们是在对第i列进行操作,所以当前状态下无法放入任何一个积木块,j的状态只能为0
综上,我们就能得到一个关于判断状态转移是否合法的二维数组。
{1,1,1,1}
{0,0,1,1}
{0,1,0,1}
{1,0,0,0}
这样我们就能通过当前列的状态推出下一列的状态是否合法。
推导dp式:
在我们使用状态推导的时候,我们首先要确定两个问题,dp式表达的含义是什么,dp公式是什么。由于这道题求的是积木的方案数,我们可以让dp式存放状态数。由于我们是一列一列去判断的,所以我们还需要记录下当前处理到了哪一列(同时也知道了前i-1处理完毕后的状态数),同时由于第i列的摆放状态会对下一列的状态转移产生影响。我们还要知道当前的状态。所以用dp[i][j]可以表示,i是当前的列数,j是当前的状态(也就是之前的状态压缩)。假设已经处理到最后一列的最后一种状态,那么当前列的状态数就应该是当前列的其他状态数加上从上一列状态转化到当前状态时上一列的状态数(必须满足状态转移的合法性,才能加上上一列的状态数),也就是dp[i+1][k] = dp[i+1][k]+f[j][k]*dp[i][j]。同样二维数组两纬度分别表示列数和当前列状态。(k是下一列的四种状态,)所以通过三层循环,一层遍历所有的列数,一层遍历当前列的所有状态,一层遍历下一列所有的状态,通过之前枚举过的状态转移合法性数组来判断是否能从当前状态转移到目标状态,如果能转移过来就可以加上当前状态的状态数,如果不能就只能加上其他目标状态的状态数。最后要注意的一点是,我们要取的结果是dp[n+1][0],因为我们在刚进入n+1列的时候才说明n列已经全部计算完毕。
代码实现:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
//假设前i列已经摆好了,j对应是第i行的状态
//采取状态压缩,用二进制的每一个位表示当前格子是否被占用,合成的十进制数就能表示当前状态。
//由于第i+1行的状态是由第i行决定的,第i行有四种状态,0 0,0 1,1 0,1 1,十进制就是0,1,2,3,第i+1行也有四种状态,所以一共有16种状态
//我们可以枚举出从第i 转移到 i+1的所有情况并判断这种情况是否存在,让状态作为下标,这样这个数组表示的就是能否从第i行转移到第i+1行,存在值为1,不存在值为0
int g[4][4] =
{
{1,1,1,1},
{0,0,1,1}, //表示能否转移到j状态的数组
{0,1,0,1},
{1,0,0,0},
};
const int N = 1e7 + 10, mod = 1000000007;
int dp[N][4]; //状态转移数组,i表示处理完i-1行,当前位于第i行,处于第j状态
int main()
{
int len;
cin >> len;
dp[1][0] = 1;
for (int i = 1; i <= len; i++) //相当于检查三排,前i-1塞满,从j状态转移到k状态
{
for (int j = 0; j < 4; j++)
{ //k表示要向k状态转移
for (int k = 0; k < 4; k++) //需要通过枚举数组判断当前状态能否转移过来
{
dp[i+1][k] = (dp[i+1][k] + g[j][k] * dp[i][j])%mod;
}
}
}
cout << dp[len+1][0]; //当我们处理到len+1的时候且当前状态为0,这意味着前len行已经铺满了,也就是我们要求的
return 0;
}