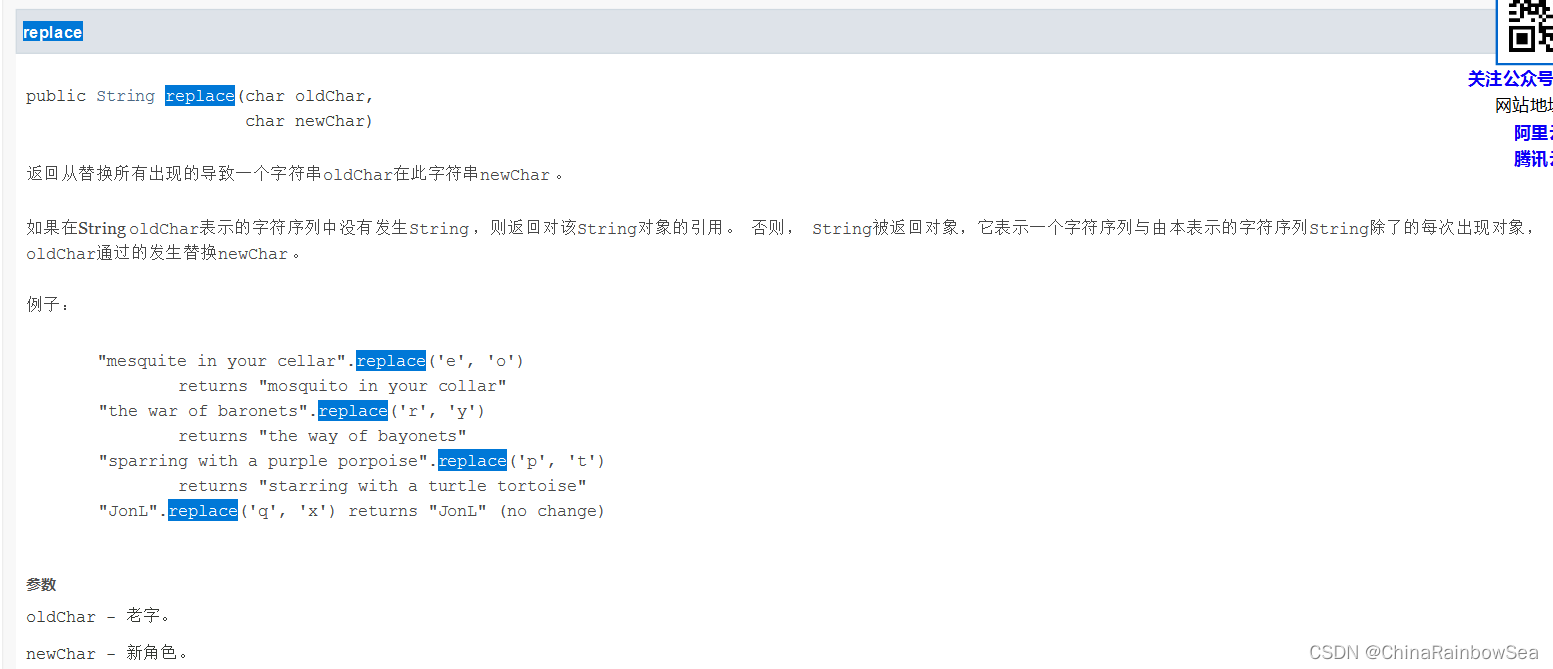
声学特征提取流程图

语谱图

语谱图的横坐标是时间，纵坐标是频率，坐标点值为语音数据能量。由于是采用二维平面表达三维信息，所以能量值的大小是通过颜色来表示的，颜色深，表示该点的语音能量越强。

语谱图形成过程

• 信号预加重

因为语音信号的功率谱随频率的增加而减小，导致语音的大部分能量都集中在低频部分，从而导致高频部分的信噪比很低。因此一般使用一阶高通滤波器去提升信号在高频部分的信噪比。对语音进行完预加重后，然后就是分帧加窗操作；

• 对信号进行分帧加窗，进行STFT， 得到每帧信号的频谱图；

对于一段语音，以10ms~30ms 为一帧，为了保证帧与帧之间平滑过渡保持连续性，帧与帧之间会有重叠。一段语音信号x(t) , 通过分帧之后， 数据由一维信号变为二维信号；分帧之后，变为x(m,n)m为帧长， 代表每一帧的长度；n 为帧的个数， n 列代 n个帧；

• 对频谱图进行旋转加映射；
• 将变换后的多帧频谱进行拼接，形成语谱图；

语谱图形成原理

频谱spectrum 的产生

将每一帧的数据都进行FFT变换（严格来讲， 每帧数据加窗后做FFT ， 称之为STFT)，由$x(m,n)$ 得到$X(m,n)$。$X(m,n)$ 称作频谱， 反应了频率与能量之间的关系。

在实际使用中，频谱图有三种，即

• 线性振幅谱
• 对数振幅谱：（对数振幅谱中各谱线的振幅都作了对数计算，所以其纵坐标的单位是dB分贝）。
• 自功率谱

这个变换的目的是使那些振幅较低的成分相对高振幅成分得以拉高，以便观察掩盖在低幅噪声中的周期信号。

语谱图作用

因为声谱图中有很多重要的特征， 比如音素特征；共振峰特征（formants 即频谱图中的峰值）以及观察他们的转变趋势， 可以更好的识别音频；

• 语音信号的时间-频率表示方法：
• 语谱图是研究语音（音素Phone）的工具
• 语音学家对音素Phone及其特性进行直观研究
• 隐马尔科夫模型隐含了语音到文本系统的语谱图模型有助于评估文本到语音系统——一个高质量的文本到语音系统应该产生合成语音，其频谱图应该与自然句子几乎一致

MFCC算法

参考地址

预加重

为了避免在后边的FFT操作中出现数值问题，我们需要加强一下高频信息，因为一般高频能量比低频小。其预加重函数如下所示：
$$y(n)=x(n)-\alpha \cdot x(n-1$$

分帧

我们要对语音数据做傅里叶变换，将信息从时域转化为频域。但是如果对整段语音做FFT，就会损失时序信息。因此，我们假设在很短的一段时间t内的频率信息不变，对长度为t的帧做傅里叶变换，就能得到对语音数据的频域和时域信息的适当表达。例如我们这里的采样点数为200000个点，如果真的这样做的话，就很麻烦了，于是我们在语音分析中引入分帧的概念，将原始语音信号分成大小固定的N段语音信号，这里每一段语音信号都被称为一帧。

但是，如果我们这样分帧的话，帧与帧之间的连贯性就会变差，于是我们每一帧的前N个采样点数据与前一帧的后N个采样点数据一样。

对于整个采样点数据可以分为多少帧以及帧与帧之间交叉的采样点个数N，不是随便分的，一般来说帧长设置为25$ms$,帧移设置为10$ms$。

$$帧数=f_s\cdot 0.025=0.025f_s(个采样点)$$

$$帧移=f_s\cdot 0.001=0.001f_s(个采样点)$$

加窗

将信号分帧后,我们将每一帧代入窗函数，窗外的值设定为0，其目的是消除各个帧两端可能会造成的信号不连续性（即谱泄露 spectral leakage）。常用的窗函数有方窗、汉明窗和汉宁窗等，根据窗函数的频域特性，常采用汉明窗（hamming window）。

$$W(n)=(1-\alpha )-a\cdot cos(2\cdot \pi \cdot \frac{n}{N}),1\le n\le N$$

梅尔滤波器

梅尔值，这是一个新的量度，相比于正常的频率机制，梅尔值更加接近于人耳的听觉机制，其在低频范围内增长速度很快，但在高频范围内，梅尔值的增长速度很慢。每一个频率值都对应着一个梅尔值，其对应关系如下

$$m=2595\cdot {\log }_{10}(1+\frac{f}{700})$$