概念引入

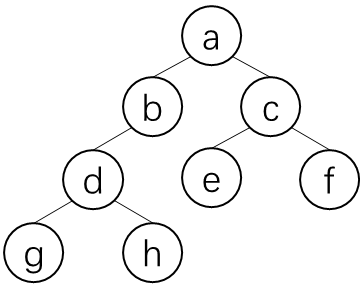
祖先

祖先其实很好理解，一个节点的 **父节点 以及 父节点的父节点 以及 父节点的父节点的父……**都是这个节点的祖先

比如说上面的 $d$ 节点， $b$ 节点和 $a$ 节点都是它的祖先

$k$ 级祖先

称节点 𝑥 的父节点为 𝑥 的 1 级祖先。节点 𝑥 父节点的 𝑘 级祖先称为节点 𝑥 的 𝑘 + 1 级祖先。

比如，节点 $a$ 就是节点 $d$ 的二级祖先

引例

假设节点 $i$ 的 $k$ 级祖先是 $j$， $j$ 的 $k1$ 级祖先为 $x$ ，那么 $x$ 为 $i$ 的几级祖先？

显然是 $（k+k1）$ 级祖先

深度

记 𝑑𝑒𝑝(𝑥) 为节点 𝑥 的深度。
若 𝑥 为根结点，则 𝑑𝑒𝑝(𝑥) = 1；
否则 𝑑𝑒𝑝(𝑥) = 𝑑𝑒𝑝(𝑓) + 1，其中 𝑓 为 𝑥 的父节点。

基本思想

考虑树上深度相同的节点对 (𝑥, 𝑦)，设其 𝐿𝐶𝐴 为节点 𝐿。
Δ = 𝑑𝑒𝑝 𝑥 − 𝑑𝑒𝑝(𝐿)
显然，Δ > 0，为节点对 (𝑥, 𝑦) 与 𝐿 的深度差，即节点 (𝑥, 𝑦)想要抵达节点 𝐿，需要向上跳跃的距离。

我们只需要求出节点 𝑥 或 𝑦 的 Δ 级祖先，就求出了节点对 (𝑥, 𝑦)的最近公共祖先，但 Δ 具体的值并不明确，采用尝试的办法。
不妨记 𝐹(𝑥, 𝑘)(𝑘 ≥ 0) 为节点 𝑥 的 $2^k$ 级祖先。
由倍增思想，从高位$(lo{g}_{2}n)$向低位($0$)依次枚举 𝑖。
若 𝐹 𝑥, 𝑖 = 𝐹(𝑦, 𝑖)，说明 𝑥 的 $2^i$ 级祖先在节点 𝐿 到根节点的路
径上，不作处理。
否则，𝑥 ← 𝐹 𝑥, 𝑖 , 𝑦 ← 𝐹(𝑦, 𝑖)。
当 𝑖 = 0 枚举完毕后，𝑥, 𝑦 节点的父节点即为其最近公共祖先。

代码实现

𝐹(𝑥, 𝑘) 则可以通过递推在预处理中求出。
$$F(x,0)=f$$
$$F(x,k)=F(F(x,k-1),k-1))$$
这可以通过一次树上遍历完成。
若 𝑑𝑒𝑝 𝑥 ≠ 𝑑𝑒𝑝(𝑦)，不妨设 𝑑𝑒𝑝(𝑥) > 𝑑𝑒𝑝(𝑦)，先通过一次倍增，将节点 𝑥 向上跳跃至与节点 𝑦 深度相同。

$Code$

#include <bits/stdc++.h>
#define ll long long
const int INF = 0x3f3f3f3f;
const int N = 5e5+10; 
using namespace std;
int n, m , s;
vector <int> e[N];
int fa[N][25],dep[N];
void get_father(int pos,int f){
	fa[pos][0] = f;
	dep[pos] = dep[f] + 1;
	for(int i = 1; i <= 20; i++){
		fa[pos][i] = fa[fa[pos][i-1]][i-1];
	}
	for(auto j : e[pos]){
		if(j == f) continue;
		get_father(j,pos);
	}
}
int LCA(int x, int y){
	if(dep[x] < dep[y]){
		swap(x,y);
	}
	for(int i = 20; i >= 0; i--){
		if(dep[fa[x][i]] >= dep[y]){
			x = fa[x][i];
		}
	}
	if(x == y) return x;
	for(int i = 20; i >= 0; i--){
		if(fa[x][i] != fa[y][i]){
			x = fa[x][i];
			y = fa[y][i];
		}
	}
	return fa[x][0];
}
int main(){
	cin >> n >> m >> s;
	for(int i = 1;i < n; i++){
		int u, v;
		cin >> u >> v;
		e[u].push_back(v);
		e[v].push_back(u);
	}	
	get_father(s,0);
	while(m--){
		int x, y;
		cin >> x >> y;
		cout << LCA(x,y) << endl;
	}
	return 0;
}