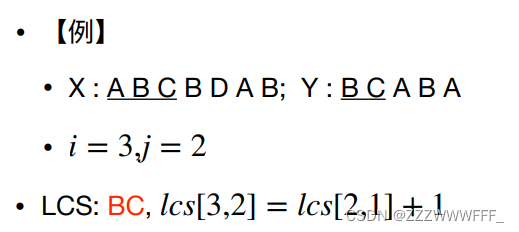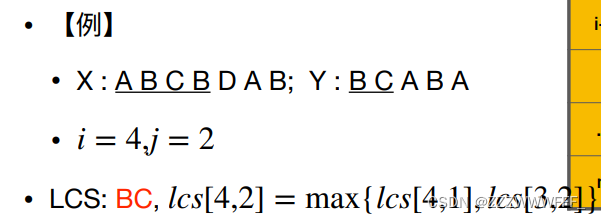Time Limit: 1 Sec     Memory Limit: 128 Mb        
Description
求两个序列的最每组测试样例都为一行，两组字符串，每组不超过1000，用空格隔开。求最长公共子序列，都为小写字母。

Input
每组测试样例都为一行，两组字符串，每组不超过1000，用空格隔开。

Output
对于每个测试实例，输出最长公共子序列的长度，每个实例的输出占一行。

Sample Input
abcfbc abfcab
programming contest 
abcd mnp
Sample Output
4
2
0

该题是算法动态规划的练习题

还是按照动态规划的步骤来

先定义子问题的存储数组，按照题目问题定义即可，很明显子问题肯定是被限制在两个输入字符串a和b各自的子字符串里，因此我们定义一个二维数组dp[i][j] 为对a的子字符串[1,i] 和 对b的子字符串[1,j] 的最长公共子序列长度

然后就是划分子问题和子问题之间的关系了（得到递推方程）

case1:

a[i] == b[j] ---> dp[i][j]=dp[i-1][j-1]+1

case2:

a[i] != b[j]  dp[i][j]=max(dp[i-1][j],dp[i][j-1]) 

这里想了蛮久理解起来还是有点困难，下面是一些分析，希望能帮助理解

假设已经知道 Zk={z1,z2,…,zk} 是X={x1,x2,…,xm} 和 Y={y1,y2,…,yn} 的最长公共子序列 

，那么可以分2种情况讨论

1）如果zk = xm = yn

        那么Zk-1是Xm-1和Yn-1的最长公共子序列

2）如果xm!=yn

        1）如果 zk!=xm

                那么Zk-1是Xm-1和Yn的最长公共子序列

        2）如果zk!=yn

                那么Zk-1是Xm和Yn-1的最长公共子序列

到这里其实就可以写代码了

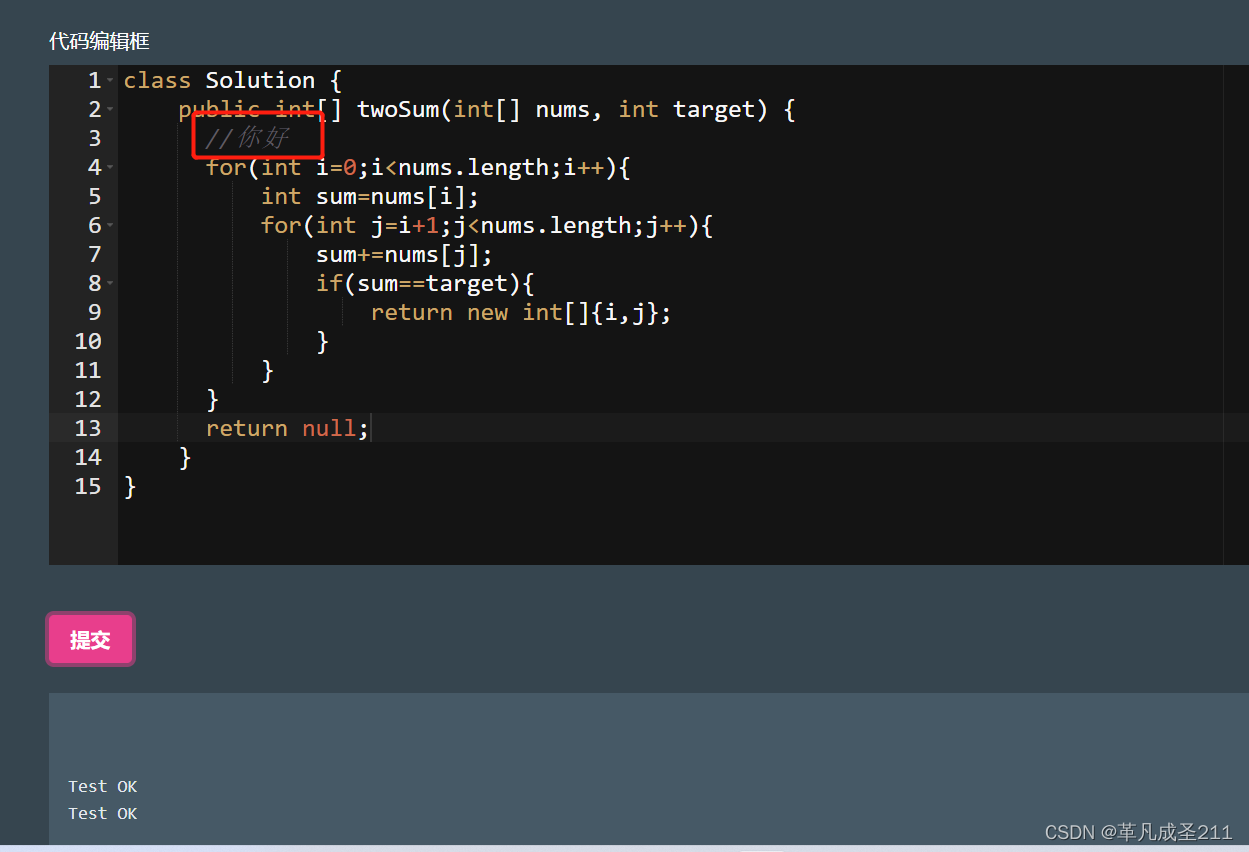
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

char a[1010],b[1010];
int dp[1010][1010];//定义dp[i][j]为对a的子字符串[1,i] 和 对b的子字符串[1,j] 的最长公共子序列长度 

int main(){
	while(scanf("%s %s",a,b)!=EOF){
		memset(dp,0,sizeof(dp));//初始化为0 
		int lena=strlen(a),lenb=strlen(b);
		for(int i=0;i<lena;i++){
			for(int j=0;j<lenb;j++){
				if(a[i]==b[j]){//为避免下标越界，这里的下标都+1 
					dp[i+1][j+1]=dp[i][j]+1;
				}else{
					dp[i+1][j+1]=max(dp[i][j+1],dp[i+1][j]);
				}
			}
		}
		printf("%d\n",dp[lena][lenb]);
	}
	
	return 0;
}