子图同构问题
子图同构(Subgraph Isomorphism)是指在图论中,两个图之间是否存在一种关系,使得其中一个图的顶点集合和边集合可以通过对应的方式映射到另一个图的顶点集合和边集合上,且保持原来的边和顶点的关系不变。
具体来说,给定两个图 G = ( V G , E G ) G=(V_G,E_G) G=(VG,EG)和 H = ( V H , E H ) H=(V_H,E_H) H=(VH,EH),若存在一种从 G G G到 H H H的映射 ϕ : V G → V H \phi:V_G\rightarrow V_H ϕ:VG→VH,满足:
对于 V G V_G VG中的任意两个不同的顶点 v i v_i vi和 v j v_j vj,如果在 E G E_G EG中有边连接它们,那么在 E H E_H EH中 ϕ ( v i ) \phi(v_i) ϕ(vi)和 ϕ ( v j ) \phi(v_j) ϕ(vj)也必须有一条边连接;
对于 V H V_H VH中的任意两个不同的顶点 v i ′ v'_i vi′和 v j ′ v'_j vj′,如果在 E H E_H EH中有边连接它们,那么在 E G E_G EG中存在 v i v_i vi和 v j v_j vj,满足 ϕ ( v i ) = v i ′ \phi(v_i)=v'_i ϕ(vi)=vi′, ϕ ( v j ) = v j ′ \phi(v_j)=v'_j ϕ(vj)=vj′,且在 E G E_G EG中也有边连接 v i v_i vi和 v j v_j vj。
如果这样的映射 ϕ \phi ϕ存在,则称图 G G G是图 H H H的子图,并称 ϕ \phi ϕ为从 G G G到 H H H的子图同构映射。
这左图与右图子图同构

存在如下映射关系:

用
M
A
,
M
B
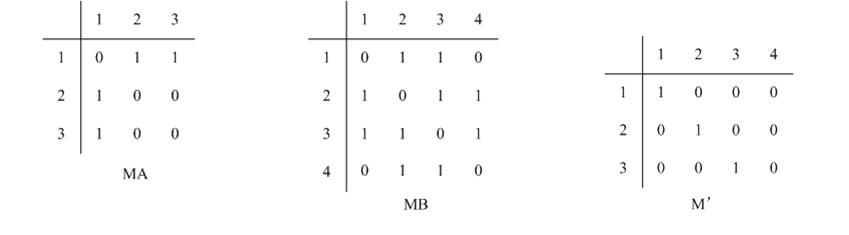
MA, M B
MA,MB分别表示左图A,和右图B的对应的邻接矩阵,其中
M
A
[
i
]
[
j
]
=
1
MA[i][j] = 1
MA[i][j]=1表示顶点
i
i
i与
j
j
j存在一条边,
M
A
[
i
]
[
j
]
=
0
MA[i][j] = 0
MA[i][j]=0表示无边
M ′ M' M′表示映射从 M A M A MA到 M B M B MB的映射矩阵, M [ i ] [ j ] = 1 M [i][j] = 1 M[i][j]=1表示A中第 i i i个顶点 v i vi vi对应到 M B M B MB中的第 j j j个顶点,否则为 0 0 0表示没有对应
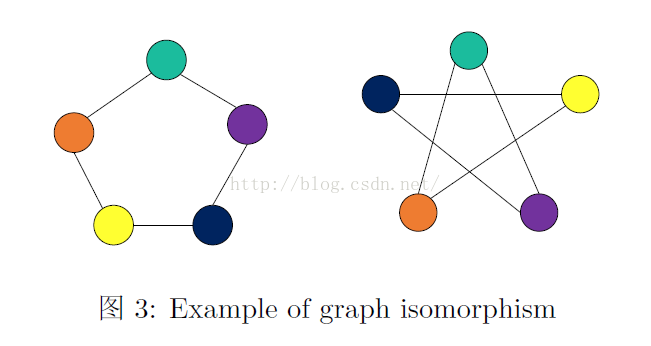
上图是一个图同构的例子,顶点之间并没有颜色区分,为了更好地看出顶点间的映射关系,加上了颜色。
子图同构在图形识别、化学结构分析、计算机视觉、网络安全等领域都有广泛应用。但是在实际问题中,子图同构问题往往是 NP 难问题,因此需要采用各种方法进行求解。
单射函数和双射函数
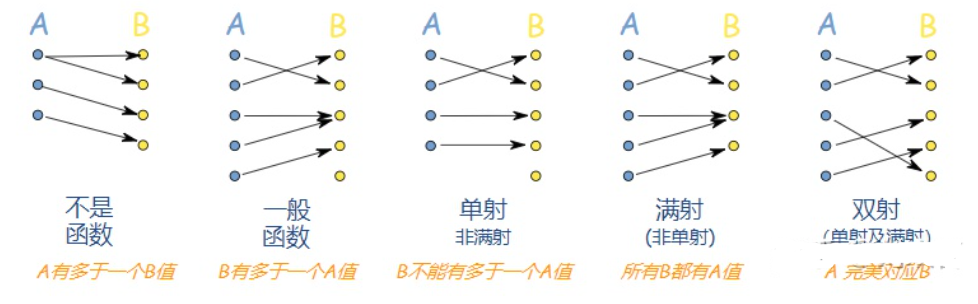
单射函数和双射函数都是函数的特殊类型。
单射函数(injective function),也称为一对一函数,是指一个函数f:A→B,其中任意一个B中的元素b,都最多只对应一个A中的元素a,即对于任意的b∈B,都有至多一个a∈A,使得f(a)=b。
双射函数(bijective function),也称为一一对应函数,是指一个函数f:A→B,其中A和B是两个集合,满足下面两个条件:
对于任意的
a
∈
A
a∈A
a∈A,都存在一个
b
∈
B
b∈B
b∈B,使得
f
(
a
)
=
b
f(a)=b
f(a)=b。
对于任意的
b
∈
B
b∈B
b∈B,都存在一个
a
∈
A
a∈A
a∈A,使得
f
(
a
)
=
b
f(a)=b
f(a)=b。
换言之,双射函数是一种既是单射函数又是满射函数的函数。
区别在于,单射函数保证了每个B中的元素最多只对应一个A中的元素,但不保证每个B中的元素都有对应的A中的元素;而双射函数则保证了每个B中的元素都有对应的A中的元素,并且每个B中的元素最多只对应一个A中的元素。
同构(isomorphic)和同态(homomorphism)
简单来讲,对于两个不带标签的无向图,假设 G 1 = ( E 1 , V 1 ) , G 2 = ( E 2 , V 2 ) G1=(E1,V1),G2=(E2,V2) G1=(E1,V1),G2=(E2,V2),如果存在一种映射关系 M M M ,使得 M ( v 1 ) ∈ G 2 , ( M ( v 1 ) , M ( v 1 ′ ) ) ∈ G 2 M(v1)∈G2,(M(v1),M(v1′))∈G2 M(v1)∈G2,(M(v1),M(v1′))∈G2,对于每个 v 1 , v 1 ′ ∈ G 1 v1,v1′∈G1 v1,v1′∈G1,那么图同态;若 M M M是一个单射函数,则 G 1 , G 2 G1,G2 G1,G2同构。该定义可以扩充到其他更复杂类型的图中。
因此,同构必定是同态的。
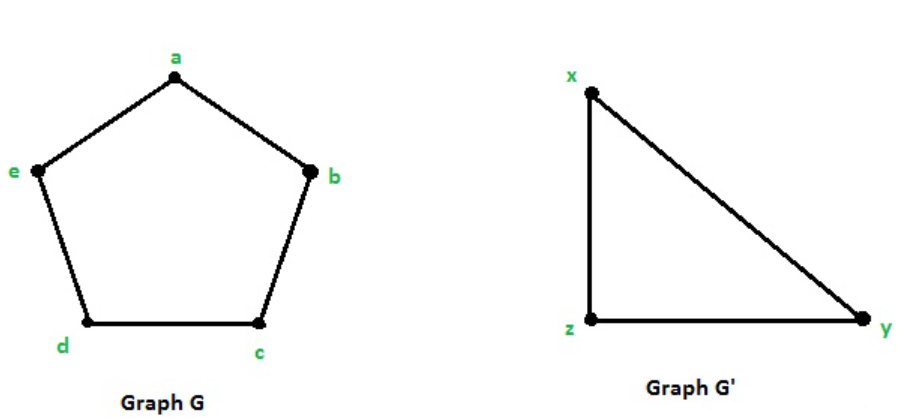
对于上面的图,是一个同态图但是不是同构图。
因为存在这样一个映射函数f满足: f ( a ) = x , f ( b ) = y , f ( c ) = z , f ( d ) = x , f ( e ) = y f(a)=x,f(b)=y,f(c)=z,f(d)=x,f(e)= y f(a)=x,f(b)=y,f(c)=z,f(d)=x,f(e)=y。显然映射函数f不是单射函数,所以这两个图同态但不同构。