互联网上有数百亿个网页，可以分为这么几类：不含有用信息的，比如垃圾邮件；少数人比较感兴趣的，但范围不是很广的，比如个人博客、婚礼公告或家庭像册；很多人感兴趣的并且十分有用的，比如社交网站、新闻网站或某个公司的网站。

如此大量的网页对搜索引擎来说是个问题，因为搜索结果可能会有百万个甚至千万个。比如，你想访问“知乎”，但是不知道它具体的URL，这时你会在搜索框里输入“知乎”两个字，假设搜索结果有几百万条，那么最热门的那一条或者说“最正确”的那一条该如何来确定呢？

一个比较有效的方法是数inlinks，以知乎为例，数有多少个链接指向它。PageRank就是基于这种链接分析(link analysis)的算法。

PageRank计算过程示例

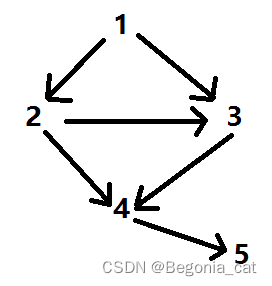
假设有三个网页，他们的结构如下：

对于网页C来说，它的PageRank表示为PR(C)，则有。因为对于C来说，它的inlinks来自于A和B。而A有两个指向外部的链接，指向C的占其中的二分之一。同理，对于

A来说，有 

PR(A)=PR(C)；PR(B)=PR(A)2

假设，每个网页的初始值为$\frac{1}{3}$,则经过几次迭代后，PageRank会收敛到某个值。过程如下：

初始值： 

PR(A)=13,PR(B)=13,PR(C)=13

第一次迭代： 

PR(A)=PR(C)=0.33,PR(B)=PR(A)2=0.17,PR(C)=PR(A)2+PR(B)=0.332+0.33=0.5

。注意：利用上一次迭代的值进行计算

第二次迭代： 

PR(A)=0.5,PR(B)=0.17,PR(C)=0.332+0.17=0.33

第三次迭代：

PR(A)=0.33,PR(B)=0.25,PR(C)=0.42

第四次迭代：

PR(A)=0.42,PR(B)=0.21,PR(C)=0.42

第n次迭代...

经过更多次的迭代后，PR值收敛在

PR(A)=0.4,PR(B)=0.2,PR(C)=0.4

PageRank的矩阵表示及计算过程

以下是python示例

import numpy as np

# 确定网页图的结构
m = int(input('网页的总个数'))
map_page = [[-1 for i in range(m)] for j in range(m)]
map_page[0][1] = 1
map_page[0][2] = 1
map_page[1][3] = 1
map_page[2][0] = 1
map_page[2][1] = 1
map_page[2][3] = 1
map_page[3][2] = 1


Pr = np.ones((m,))/m
print('原始页面重要性初始化：\n')
print(Pr)

n = int(input('经过多少次迭代：'))
for k in range(n):
    new_Pr = [0 for i in range(m)]
    d = [0 for i in range(m)]
    for i in range(m):

        for j in range(len(map_page[i])):
            # 统计第i个节点的出度
            if map_page[i][j] == 1:
                d[i] += 1
    for i in range(m):
        for j in range(len(map_page[i])):
            if map_page[j][i] == 1:
                new_Pr[i] += Pr[j]/d[j]
    print(f'经过{k+1}次迭代以后的结果为：\n')
    Pr = new_Pr.copy()
    print(Pr)

print(f'经过{n}次迭代以后的结果为：\n')
print(Pr)