有向图及相关算法

1 有向图的实现

有向图的的应用场景

• 社交网络中的关注
• 互联网连接
• 程序模块的引用
• 任务调度
• 学习计划
• 食物链
• 论文引用
• 无向图是特殊的有向图，即每条边都是双向的

改进Graph和WeightedGraph类使之支持有向图

• Graph类的改动
• WeightedGraph类的改动

2 有向图算法

有些问题，在有向图中不存在，或者我们通常不考虑

• floodfill
• 最小生成树
• 桥和割点
• 二分图检测

有些问题，在无向图和有向图中是一样的

• DFS的代码迁移到有向图完全不用改，测试代码

  

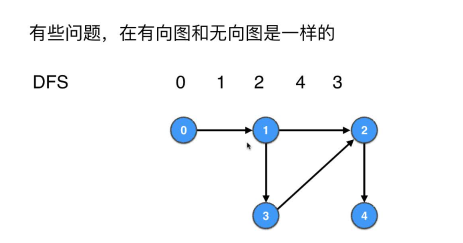
• BFS的代码迁移到有向图完全不用改，测试代码

  

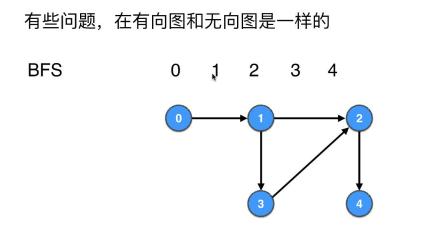
• BFS用来求无向无权图最短路径的代码用来求有向无权图也完全不用改

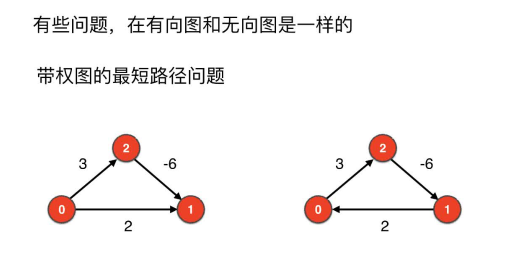
有向有权图的最短路径

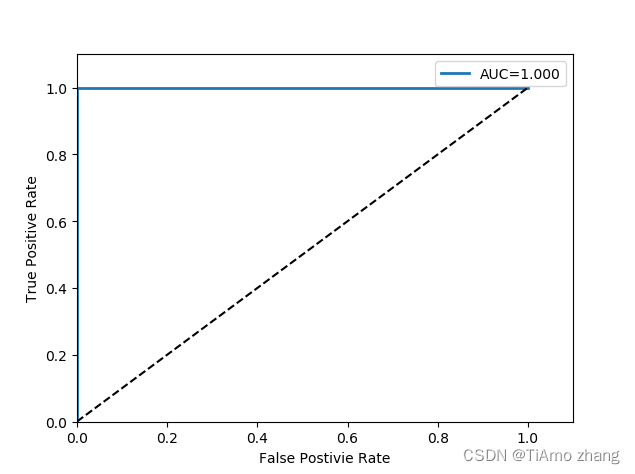
无向有权图有负权边一定有负权环；有向有权图有负权边不一定有负权环。所以最短路径问题针对有负权边的无向有权图没有意义，但是对有负权边的有向有权图可能是有意义地。

上面图片中，左右两边都是有向有权图，左边的图不存在负权环，右边的图就存在负权环，所以有向有权图中有负权边不一定有负权环

• Bellman-Ford算法测试
• Floyd算法测试

3 有向图环检测和DAG

原理

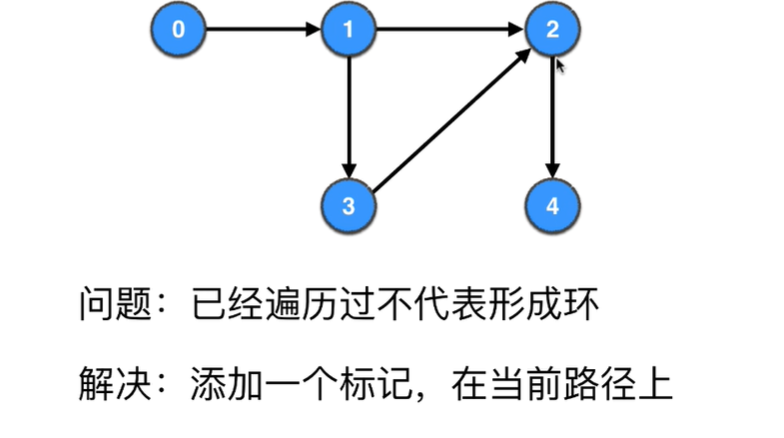
无向图中的环的判定方法在有向图中不适用，通过在遍历过程中添加标记即可，递归回退时取消对应顶点的标记

实现

• 实现代码
• 测试代码

有向图环检测的现实意义

现实中很多场景都是追求有向无环图(Directed Acyclic Graph即DAG)的

• 程序模块的循环引用检测
• 任务调度冲突检测
• 学习计划

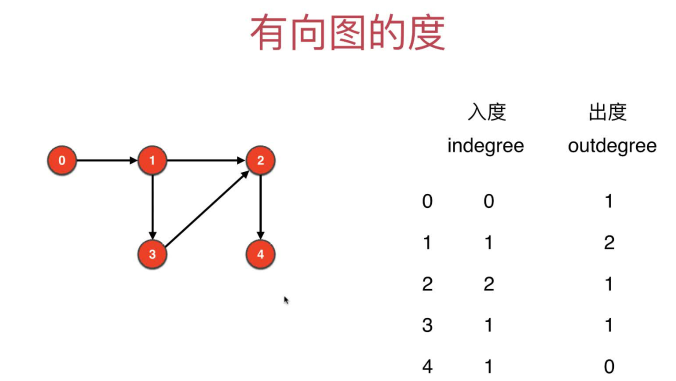
4 有向图的度：入度和出度

举例

对Graph类的修改和测试

• 对Graph类的修改
• 对修改后的Graph类的测试

5 有向图求解欧拉回路

和无向图进行比较

对比项	无向图	有向图
存在欧拉回路的充要条件	每个点的度数为偶数	每个点的入度等于出度

寻找有向图欧拉回路的代码

• 递归实现
• 非递归实现
• 测试代码

寻找欧拉路径的充要条件

主要是无向图和有向图的对比

对比项	无向图	有向图
存在欧拉路径的充要条件	除了两个点(起始点和终止点)两个点的度数为奇数，其余每个点的度数为偶数	除了两个点(起始点和终止点)，其余每个点的入度等于出度。这两个点，起始点出度比入度大1，终止点入度比出度大1

6~7 拓扑排序–仅针对有向图

拓扑排序的定义和应用价值

• 定义：在一个有向图中，对所有的节点进行排序，要求没有一个节点指向它前面的节点，最终的排序结果就是拓扑排序
• 价值：当现实中存在图状约束时，要你给出一个约束下可行的图遍历方便，这个时候拓扑排序就用上了~比如选课、选旅游路线等

原理

删除入度为0的顶点，然后删除这个和顶点连接的边，更新剩下顶点的入度；然后再删除剩下顶点中入度为0的顶点，删除这个顶点和这个顶点连接的边，更新剩下顶点的入度…一直到图中没顶点，拓扑排序就完成了，按照删除顺序得到的顶点列表就是拓扑排序结果。

过程模拟(不短寻找、删除和更新入度为0的顶点)

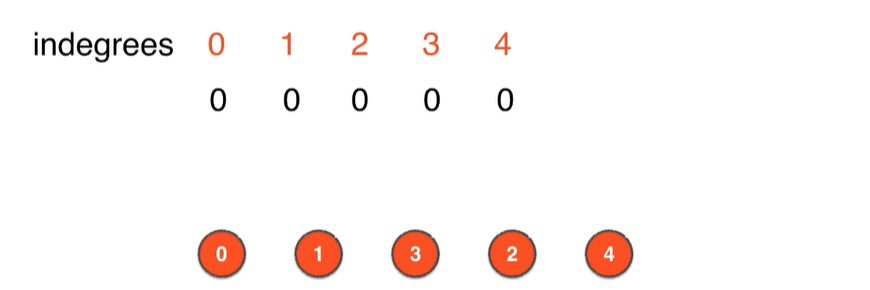
• 1.初始化计算得到各个顶点的入度inDegrees数组

  

• 2.删除此时图中入度为0的顶点即顶点0，并删除和顶点0相连的边0->1，更新删除边影响的其他顶点的入度，即把顶点1的入度更新为0

  

• 3.删除此时图中入度为0的顶点即顶点1，并删除和顶点1相连的边1->2、1->3，更新删除边影响的其他顶点的入度，即把顶点2的入度更新为1、顶点3的入度更新为0

  

• 4.删除此时图中入度为0的顶点即顶点3，并删除和顶点3相连的边3->2，更新删除边影响的其他顶点的入度，即把顶点2的入度更新为0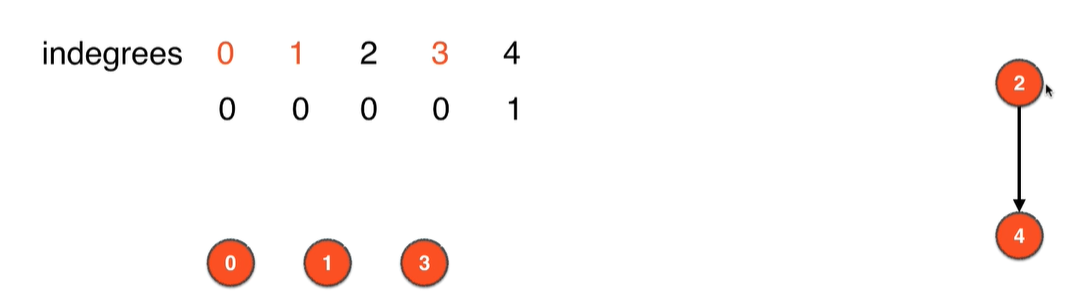

  

• 5.删除此时图中入度为0的顶点即顶点2，并删除和顶点2相连的边2->4，更新删除边影响的其他顶点的入度，即把顶点4的入度更新为0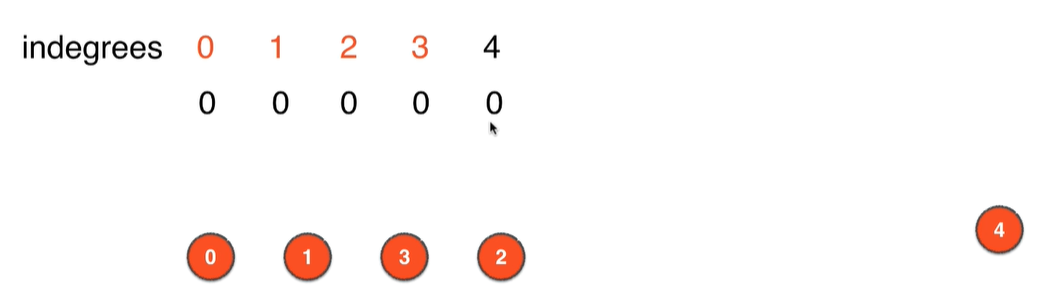

  

• 6.删除此时图中入度为0的顶点即顶点4，此时图中已经没有顶点，拓扑排序完成，上面节点删除的顺序即拓扑排序的结果，即[0, 1, 3, 2, 4]

  

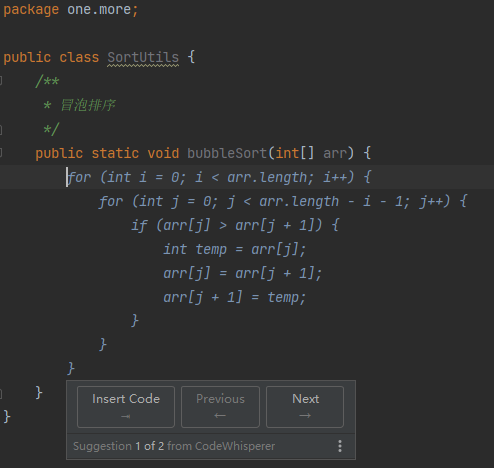
代码实现侧层面的优化

• 删除边和点不一定要真删除，可以深度clone后只更新入度即可~
• 使用队列记录当前入度为0的顶点，每次更新入度值时一般会把一个以上的更新后入度为0的顶点放入一个队列，每次从队列中取出一个点作为拓扑排序的下一个定点

拓扑排序可能无解

如下图,相当于1、2、3有循环依赖的关系_{虽然此时拓扑排序无解，但是正好可以用于有向图的环检测。只有`有向无环图即DAG`才有拓扑排序}

代码实现

• 实现代码
• 测试代码

LeetCode上的相关题目

• 207.课程表
• 210.课程表2

8~9 拓扑排序的另一种方法，方便后续学习有向图的强联通分量

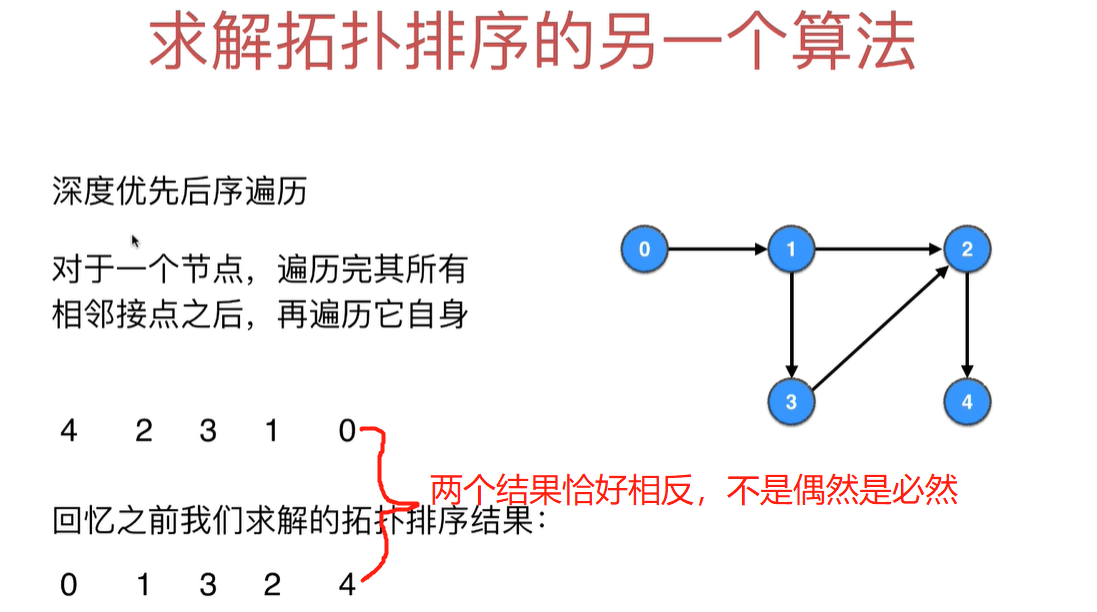
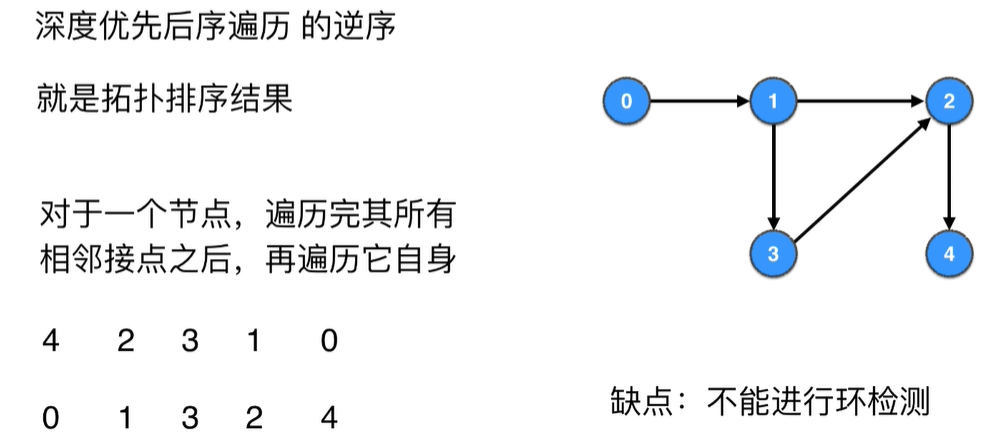
用到了图的DFS的后序遍历,自己复习下

重要结论：深度优先后续遍历的逆序就是拓扑排序的结果

缺点是不能做环检测，所以我们给这个算法的图必须是有向无环图

代码实现和测试

太简单，直接调用前面的图的DFS的后序遍历代码了

• 代码实现和测试

10~12 有向图的强联通分量

有向图因为有方向，相似的的图对无向图是连通图，对有向图就不是

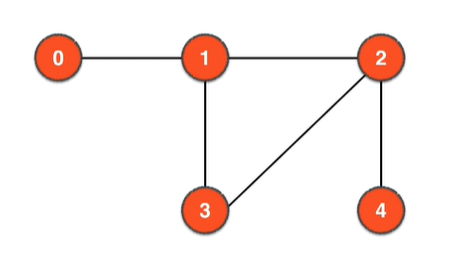
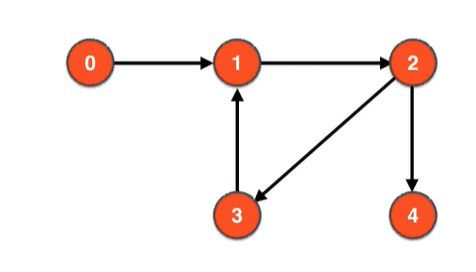
有向图的强联通分量

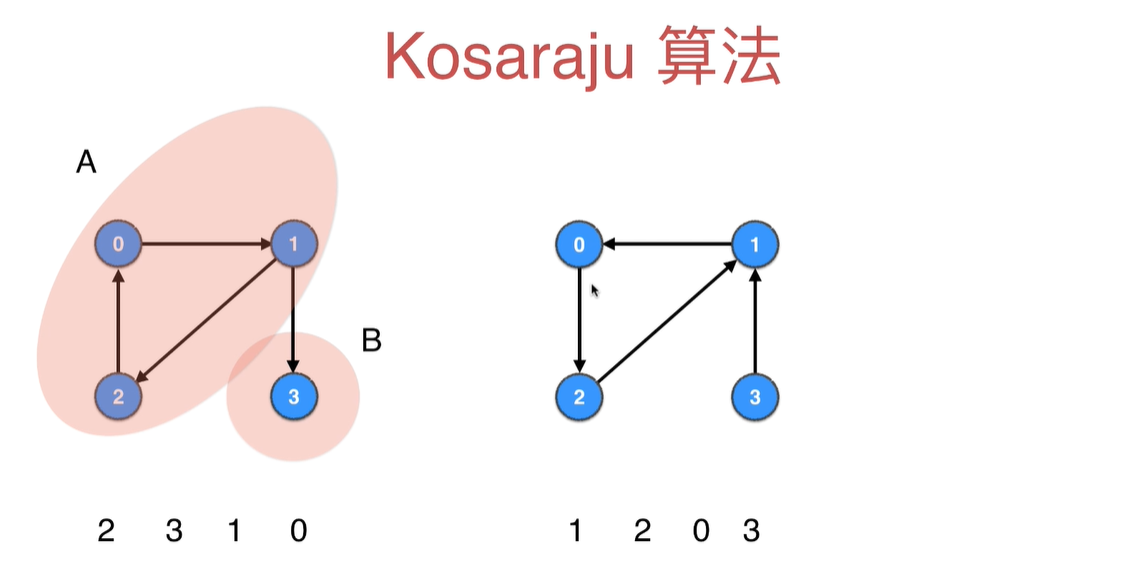
在一个有向图中，任何两点都可达的联通分量就叫强联通分量。如下图中的1、2、3组成强联通分量

将所有强联通分量看做一个点，得到的图一定是DAG(有向无环图)

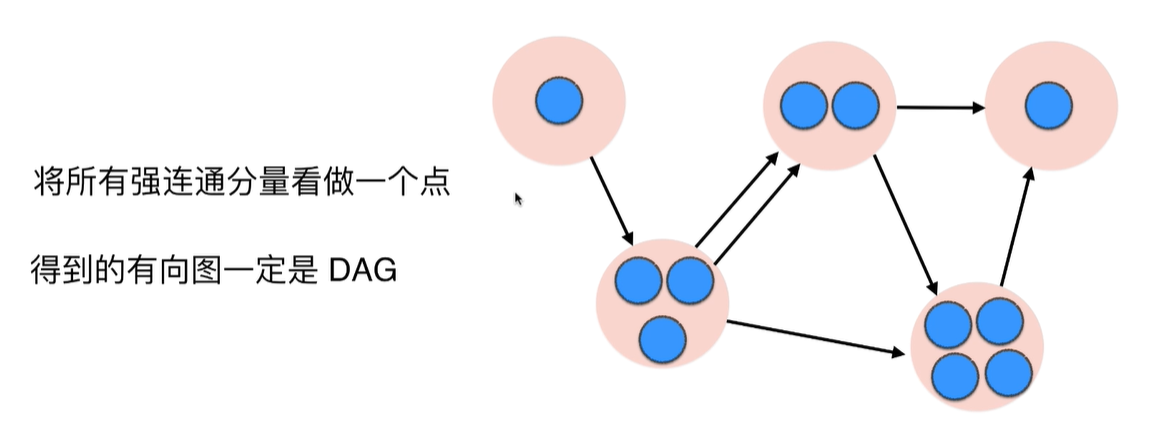
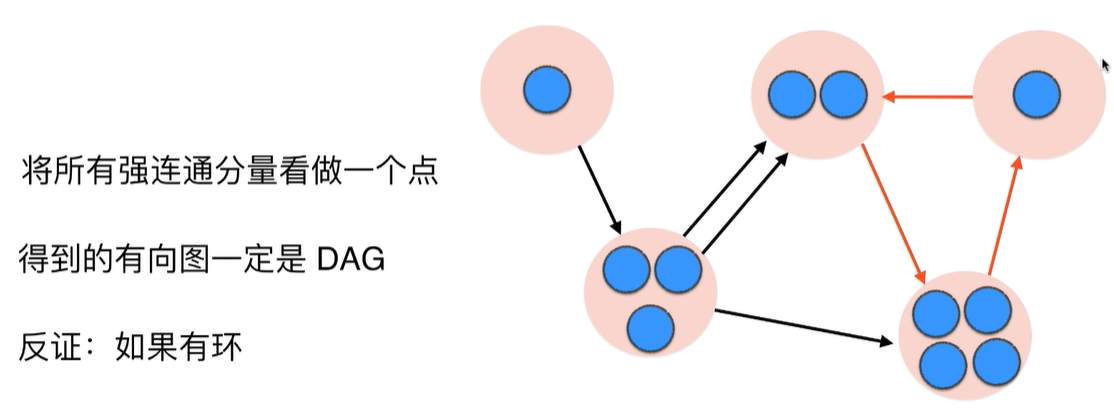
证明：反证法，如果有几个强联通分量看做的点组成了环，那么这个环还可以一个强联通分量，和我们最初的假设"所有的强联通分量各自看做一个点"矛盾。

求强联通分量各自含有的点和一共有的强联通分量个数

DFS一旦走入一个强联通分量就出不来(因为每个强联通分量一定是个环，DFS只会在环里绕圈)~~可以作为找到一个强联通分量的标志

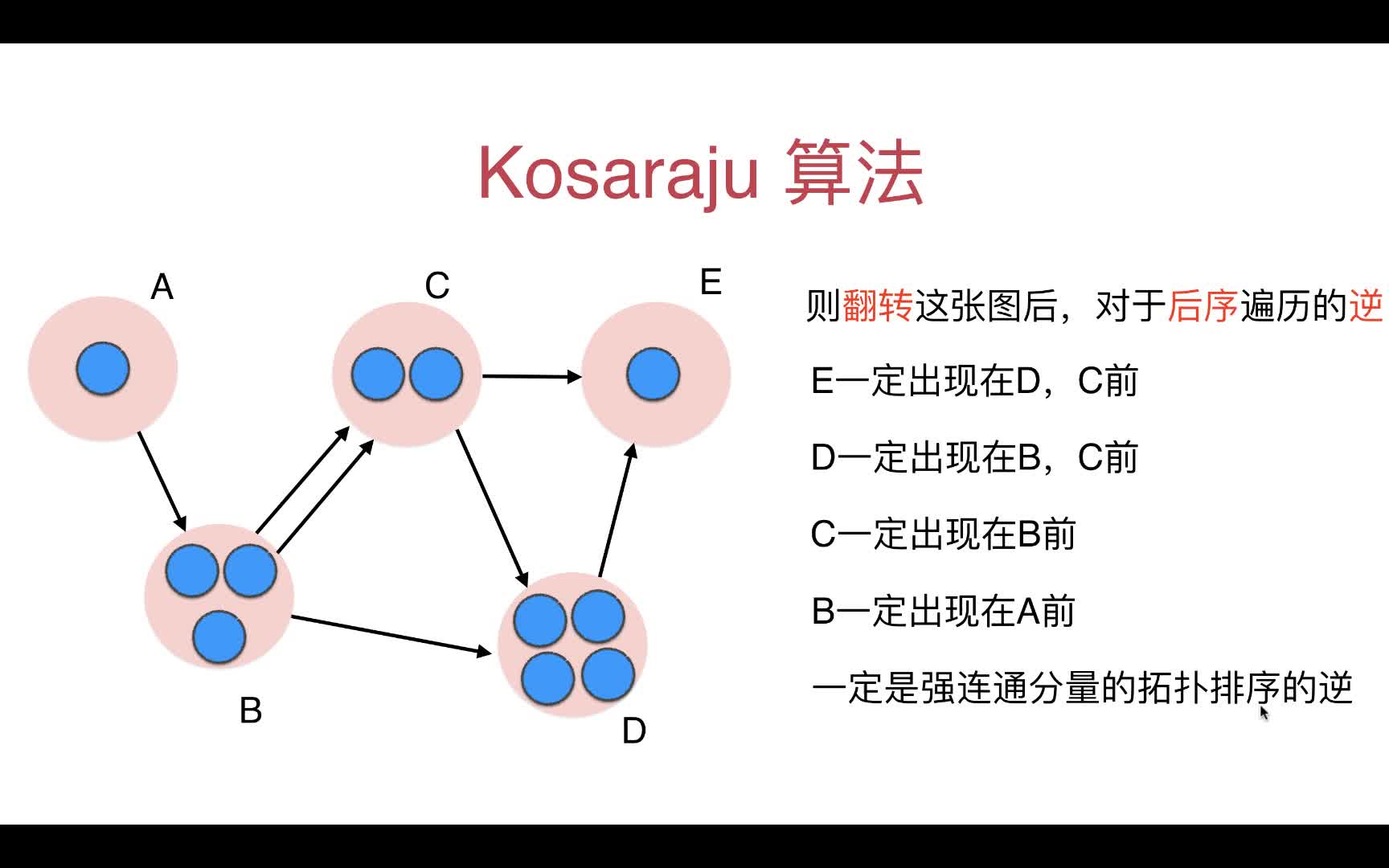
11~12 Kosaraju算法

为了解决DFS后序遍历不是我们想要的强联通分量各自分开的结果

我们上来先把原有的图每条边进行反向处理(v->w)变成(w->v)，在进行DFS后序遍历的结果就是我们想要地了

Kosaraju算法阐述

举例如下：

代码实现：略

后面有需要再搞吧

13 有向图算法总结

在无向图中存在，但是在有向图中不存在或者我们通常不考虑地

• floodfill
• 最小生成树
• 桥和割点
• 二分图检测

在有向图和无向图中完全一样的算法

• DFS、BFS
• 最短路径：Dijkstra
• 最短路径：Bellman-Ford
• 最短路径：Floyd

有向图和无向图不一样的算法

• 有向图的环检测
• 有向图的度
• 欧拉回路、欧拉路径

有向图特有的问题

• 拓扑排序：TopoSort
  • 入度+队列实现
  • 顺便做环检测
  • 时间复杂度O(V+E)
• 强联通分量
  • Kosaraju算法，简单说就是反图的DFS后续的逆序做CC
  • 时间复杂度是O(V+E)