一、背景

学习机器学习过程中，总是会遇到交叉熵这个名词。通过交叉熵损失作为损失函数来优化模型也是学习过程中必然会遇到的场景。但是,每次当和同门或者其它人遇到或者讨论什么是交叉熵的时候，总是无法从0到1讲出来，往往就是说这句话：“衡量预测结果和标签之间的分布差异，从而优化模型，使得我们的模型预测的结果能够与真实结果同分布。”
本文出于此目的，想要把交叉熵从原理到机器学习中的应用捋一遍，方便以后回顾以及和网上的你们进行不断的探讨学习。

二、概率论基础知识

1. 随机变量
   随机变量，随机变量可以取很多值，但和我们之前了解到的变量不同，随机变量无法求解。随机变量通常用大写字母表示，例如X，Y。这样的目的可能就是为了和传统的变量区分开。但是我们将其称之为变量又会对人误导，它其实是一种函数，将随机过程映射到实际数字中。比如说我想量化一个随机过程是，明天是否会下雨。你可以等到明天来看，也可以来量化。你可以定义一个随机变量，如果明天下雨就是1，如果不下就是0，不一定赋值0或者1，只是0或者1更好用而已。我们可以赋值21和100，这取决于你如何定义。随机变量和一般变量的差别要牢记，它并非传统观念意义上的变量，更像是从随机过程（下雨或者不下雨这个随机过程）映射到数值的函数，这个数值是随机的，获取我们知道概率的话，就可以将值映射为概率。
   
   
   随机抛硬币是一个随机过程，每抛一次都是一次试验。随机变量可以用来量化这个随机试验。 简单来说，随机变量就是函数映射，这里讲到的随机变量的概念将会和概率结合起来，形成非常有用的知识架构。对随机变量的量化的意义就在这里。
   
   
   
   
   

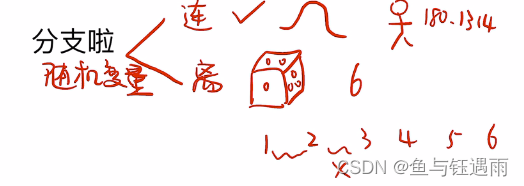
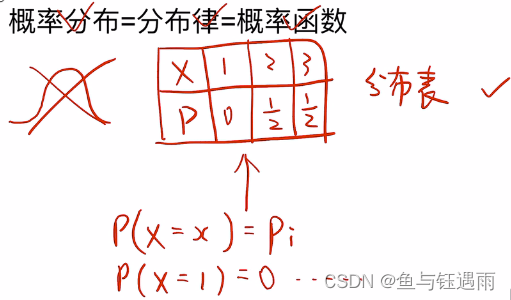
离散型随机变量X的概率分布=分布律=概率函数；
而离散型随机变量的概率分布函数F(x)就是把概率函数累加，因此又称之为累积概率函数；

三、熵≈信息熵（应用领域不同）、相对熵=KL散度、交叉熵、softmax、sigmoid、交叉熵损失

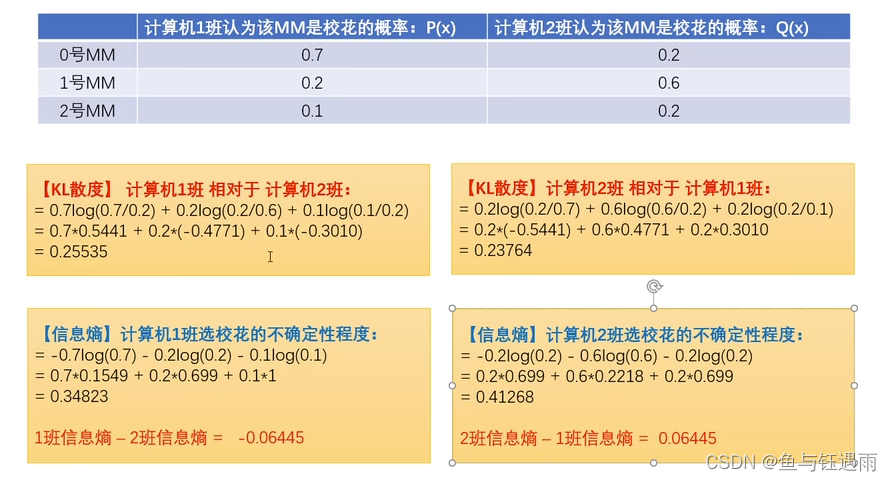
举例加深对交叉熵的理解：

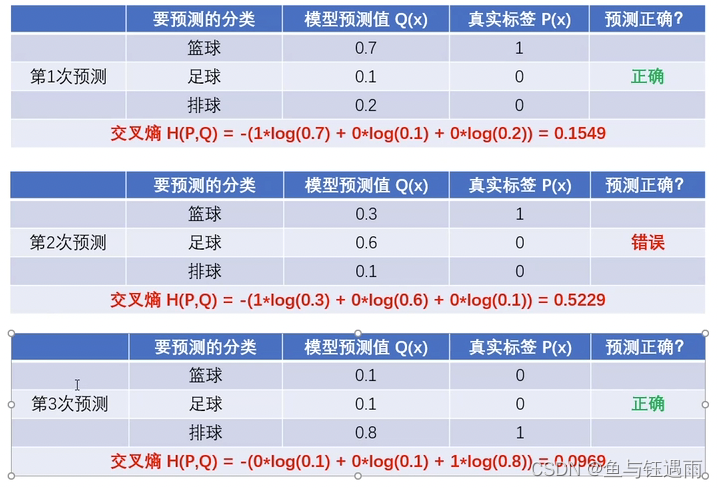
从例子中可以看出，给出的正确预测概率值越高的那个预测，标签对预测结果的交叉熵其实是最小的。

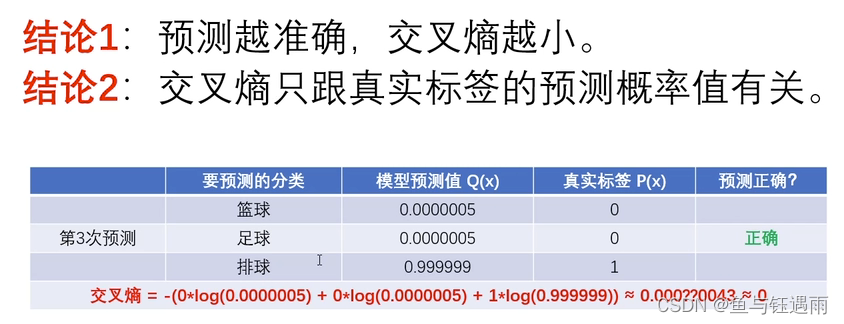
补充：0*任何数都是零；真是标签使用one hot编码的意义就是，表示的是随机变量（样本）的概率分布；交叉熵对于连续变化的信号（连续型随机变量的信号的效果是很差的，连续的一般用均方差），离散型一般用交叉熵，效果也较好。

$q(c_i)$代表预测为真实标签的概率。

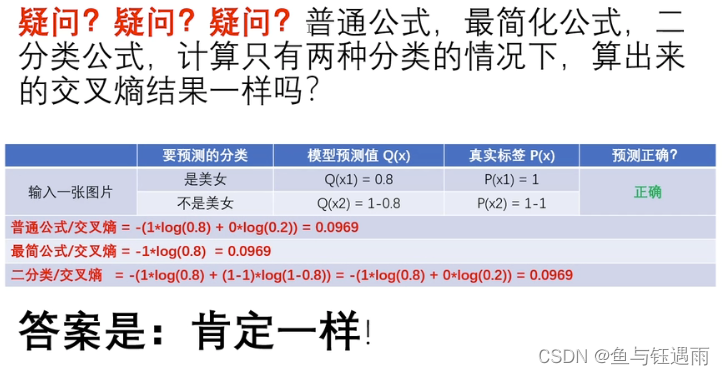
补充：（源自深度之眼：Line讲解）


其中lg和log在计算机中默认是以10为底。

图像分割如何理解CrossEntropyLoss()

其实就是像素级别的分类问题，对每个像素分类结果求交叉熵之后，求和取平均。
参考内容：pytorch语义分割中CrossEntropyLoss()损失函数的理解与分析

参考资料

bilibili一个视频彻底搞懂交叉熵、信息熵、相对熵、KL散度、交叉熵损失、交叉熵损失函数、softmax

【公开课-85集全】可汗学院：统计学（强烈推荐）