题目描述

作为一位web开发者， 懂得怎样去规划一个页面的尺寸是很重要的。 所以，现给定一个具体的矩形页面面积，你的任务是设计一个长度为 L 和宽度为 W 且满足以下要求的矩形的页面。要求：

你设计的矩形页面必须等于给定的目标面积。 宽度 W 不应大于长度 L ，换言之，要求 L >= W 。 长度 L 和宽度 W 之间的差距应当尽可能小。 返回一个 数组 [L, W]，其中 L 和 W 是你按照顺序设计的网页的长度和宽度。

示例1：

输入: 4 输出: [2, 2] 解释: 目标面积是 4， 所有可能的构造方案有 [1,4], [2,2], [4,1]。 但是根据要求2，[1,4] 不符合要求; 根据要求3，[2,2] 比 [4,1] 更能符合要求. 所以输出长度 L 为 2， 宽度 W 为 2。 示例 2:

输入: area = 37 输出: [37,1] 示例 3:

输入: area = 122122 输出: [427,286]

提示:

1 <= area <= 107

来源：力扣（LeetCode） 链接：https://leetcode.cn/problems/construct-the-rectangle 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

题目解读：找最接近的公因数

要求公因数乘积为a且差值最小

法1

1. 找公因数
   取余法找因数,就是判断是否会被整除,
2. 找出另一个因数
   除以刚刚的因数
   因为要查找最小的差值,所以范围要在前一次的两个数之间.

• 时间复杂度(O(n))
• 空间复杂度(O(1))

法2

• 时间复杂度(O())
• 空间复杂度(O())

执行结果

法1

// 最接近的两个公因数
func constructRectangle(area int) []int {
 a := [2]int{area, 1}
 for i := 2; i < a[0]; i++ {
  if area%i == 0 {//找因素
   a[0] = area / i//第二个因素
   a[1] = i
  }
 }
 return a[:]
}

执行结果： 通过 显示详情 查看示例代码 添加备注

执行用时： 60 ms , 在所有 Go 提交中击败了 26.09% 的用户 内存消耗： 1.8 MB , 在所有 Go 提交中击败了 56.52% 的用户 通过测试用例： 52 / 52

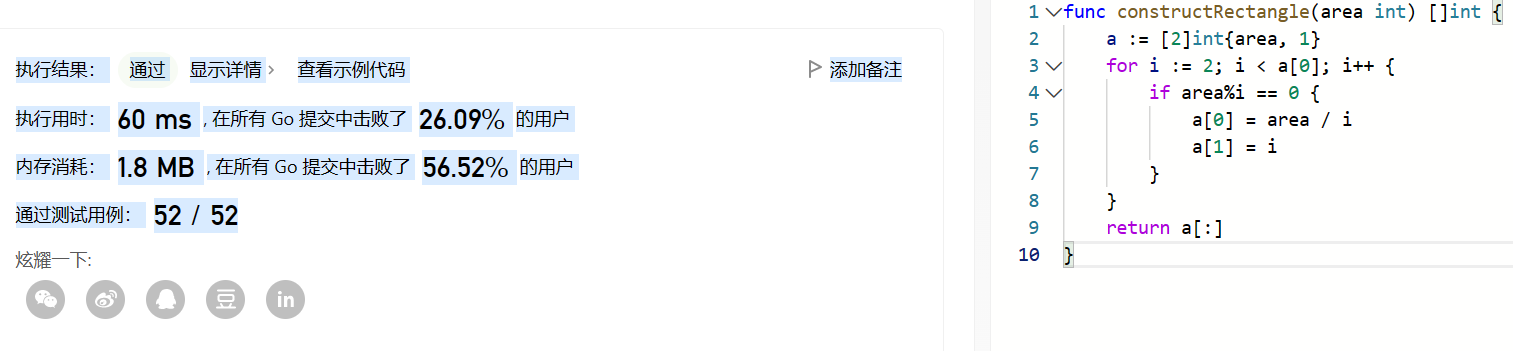
法2

法3