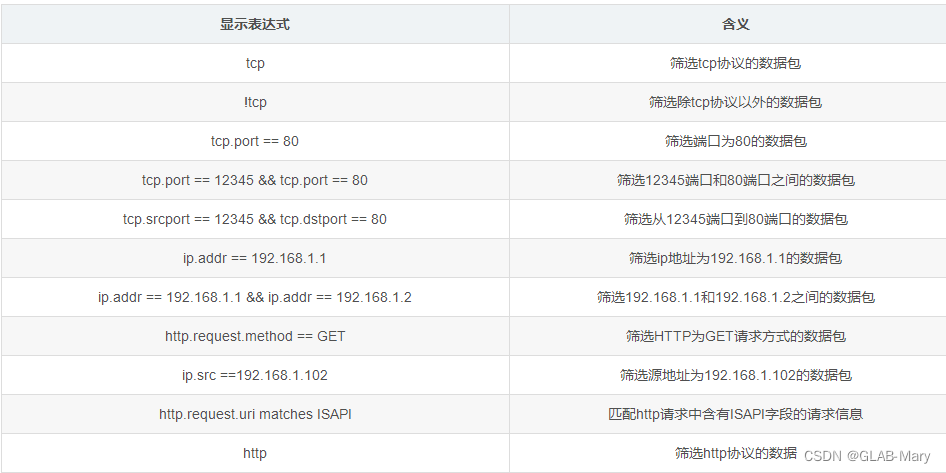
还是学过的,主要用于复习q v q
一、最小生成树
最小生成树的定义
用于无向图中,无向图指的是没有带方向路径的图,给定n个点,m条边,如果将这些点依次相连,求出连接这些点的最小数值
应用场景
根据这个算法特性,我们不能猜出此算法主要运用于要在n个城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信,但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同,因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。
prim算法
此算法主要是通过选点来进行操作的
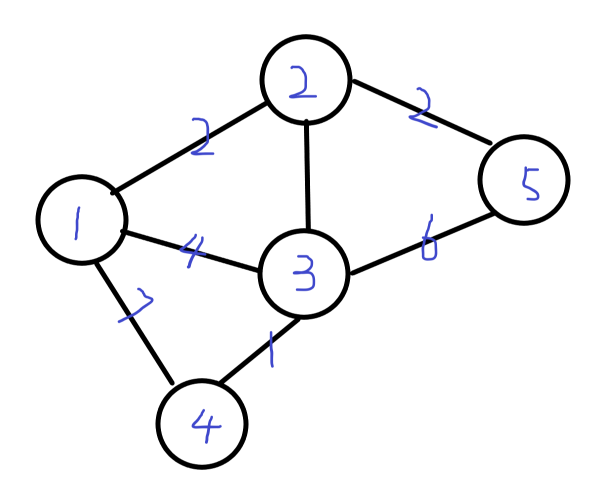
例如此图,用一维数组a来存点,二维数组b来存路径,若从 1 点开始
a[ 2 ] = 2 a[ 3 ] = 4 a[ 4 ] = 7;
选择最小的边的点,就是点 2,那么将 1 ,2 的能连接的边关系为
a[ 3 ] = 1(因为 1 到 3 的路径太长,因此 3 的路径改为 1 )
a[ 5 ] = 2
选择最小边的点,就是点 3,那么将 1 ,2,3 的能连接的边关系为
a[ 4 ] = 1(因为 1 到 4 的路径太长,因此 4 的路径改为 1 )
a[ 5 ] = 2(不变)
因此最终为
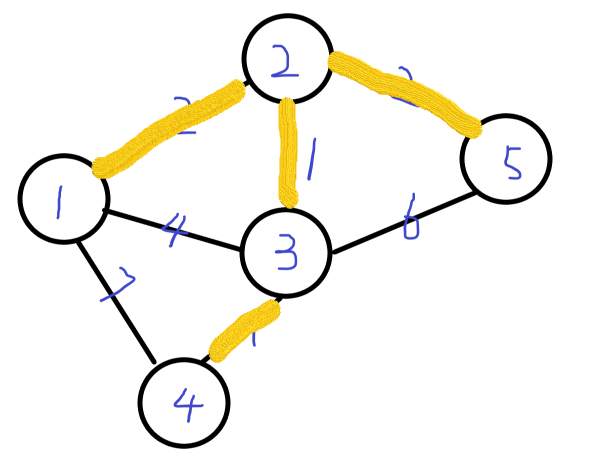
核心代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
using namespace std;
#define INF 0x3f3f3f3f //超大数
int N; // 储存图
int map[105][105]; // 顶点有没有被访问
bool book[105]; // 存储大圈圈
int lenth[105];
int Prime()
{
memset(book, false, sizeof(book)); //初始化
int sum = 0;
book[0] = true;
// 选中了0这个点,0到n个点的边权
for (int i = 1 ; i < N ; i++) {
lenth[i] = map[0][i];
}
for (int i = 1 ; i < N ; i++)
{
int min = INF;
int node;
for (int j = 1 ; j < N ; j++)
{
if (book[j] == false && lenth[j] < min)
{
//记录最小的边权值
min = lenth[j];
//记住这个最小的边的下标
node = j;
}
}
//得到大圈圈中的最小边,讲其加入到最小边边
sum += min;
//更新到了的顶点
book[node] = true;
for (int i = 1 ; i < N ; i++)
{
if (book[i] == false && lenth[i] > map[node][i]) {
lenth[i] = map[node][i];
}
}
cout << i;
}
return sum; //返回最短边权和
}
int main()
{
while (cin >> N)
{
for (int i = 0 ; i < N ; i++)
{
for (int j = 0 ; j < N ; j++) {
scanf("%d", &map[i][j]); //输入邻接矩阵
}
}
cout << Prime() << endl;
}
return 0;
}kruskal算法
kruskal算法也没啥好说的了,也就是将边权排序,依次选最小的边,当选的边等于点的数量 - 1的时候就结束,但是在这过程要注意不要围成圈了,因此就需要并查集解决这个问题,那么直接上代码吧
代码模板
#include <bits/stdc++.h>
using namespace std;
int n, m, v, k, ans, fa[10000001];
struct node //定义结构体存图
{
int x;
int y;
int z; //z表示x连y的权值
}stu[100001];
//并查集
int find(int x)
{
if (x != fa[x]){
fa[x] = find(fa[x]);
}
return fa[x];
}//查找
void unity(int x, int y)
{
int r1 = find(x);
int r2 = find(y);
fa[r1] = r2;
}//合并
bool cmp(node a, node b) //从小到大结构体排序
{
return a.z < b.z;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++){ //并查集初始化
fa[i] = i;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
scanf("%d", &v);
if (j > i) //邻接矩阵上下对称,存一半就行了
{
m++;
stu[m].x = i;
stu[m].y = j;
stu[m].z = v;
}
}
}
sort(stu + 1, stu + m + 1, cmp); //排序
for (int i = 1; i <= m; i++)
{
if (find(stu[i].x) != find(stu[i].y)) //不能连自己
{
ans += stu[i].z;//加上最小生成树中边的权值
unity(stu[i].x, stu[i].y);//连接起来
k++;//记录边数
if (k == n - 1)//n - 1条边就行了
{
printf("%d", ans);
return 0;
}
}
}
return 0;
}二、最短路径
最短路径的定义
最短路径一般用于有相同,就是带有方向的路径图
在一个图中,会出现这样的问题,要求你求出一个点到各个点的最短的路径,而这时你可能会想,那这个是不是跟那个最小生成树是不是就是一样的呢?其实不然,最小生成树是连接各个点形成的最小路径,而最短路径则是俩个点之间的最短路径,是不相同的。
迪杰斯特拉算法(dijkstra)
基本思想
首先假定源点为u,顶点集合V被划分为两部分:集合 S 和 V-S。 初始时S中仅含有源点u,其中S中的顶点到源点的最短路径已经确定。
集合S 和V-S中所包含的顶点到源点的最短路径的长度待定,称从源点出发只经过S中的点到达V-S中的点的路径为特殊路径,
并用dist[]记录当前每个顶点对应的最短特殊路径长度。
那么具体的图解我感觉在http://t.csdn.cn/HV7ku
这里面已经写的够清楚了,所以这次就偷个懒,再附赠一张大佬的动态图吧

代码模板
#include<stdio.h>
#include<iostream>
using namespace std;
#define SIZE 110
#define INF 1000000 //相当于无穷大,判断点与点的连接时需要
int map[SIZE][SIZE]; //邻接矩阵存储
int dis[SIZE]; //d[i]表示源点到i这个点的距离
int visit[SIZE]; //节点是否被访问
int n, m, j, pos, ans, temp = INF;
int dijkstra(int from, int to) //从源点到目标点
{
int i;
for (i = 1; i <= n; i++) //初始化
{
visit[i] = 0; //一开始每个点都没被访问
dis[i] = map[from][i]; //先假设源点到其他点的距离
}
for (i = 1; i < n; ++i) //对除源点的每一个点进行最短计算
{
int min = INF; //记录最小len[i]
//记录小len[i] 的点
for (j = 1; j <= n; ++j) {
if (!visit[j] && min > dis[j]) {
pos = j;
min = dis[j];
}
}
visit[pos] = 1;
for (j = 1; j <= n; ++j)
{
//如果j节点没有被访问过&&j节点到源节点的最短路径>pos节点到源节点的最短路径+pos节点到j节点的路径
if (!visit[j] && (dis[j] > (dis[pos] + map[pos][j]))) {
dis[j] = dis[pos] + map[pos][j]; //更新j节点到源节点的最短路径
}
}
}
return dis[to];
}
int main() {
int i, j;
// scanf("%d%d",&n,&m); //输入数据
//测试数据
n = 6;
m = 9;
for (i = 1; i <= n; ++i) { //设一开始每个点都不可达
for (j = 1; j <= n; ++j) {
map[i][j] = INF;
}
}
/* int a,b,c; //输入数据
for(i = 1 ; i <= m ; ++i){
scanf("%d%d%d",&a,&b,&c);
map[a][b] = map[b][a] = c;
} */
//测试数据
map[1][2] = 7;
map[1][3] = 9;
map[1][6] = 14;
map[2][3] = 10;
map[2][4] = 15;
map[3][6] = 2;
map[5][6] = 9;
map[4][5] = 6;
map[3][4] = 11;
/* 这里的一步完全不用的,多此一举而已,是判断双向边的
for (i = 1 ; i <= n ; ++i) {
for (j = 1 ; j <= n ; ++j) {
if (map[i][j] == temp)
map[i][j] = map[j][i];
}
}*/
printf("%d", ans = dijkstra(2, 5));
return 0;
}