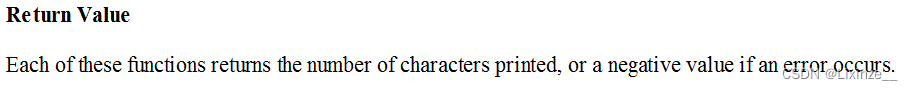【C语言】函数详解（嵌套调用和链式访问、声明及定义、递归）

news2025/1/16 7:19:34

简单不先于复杂，而是在复杂之后。

1.函数的嵌套调用和链式访问

1.1 嵌套调用

1.2 链式访问

2. 函数的声明和定义

2.1 函数声明

2.2 函数定义

3. 函数递归

3.1 什么是递归？

3.2 递归的两个必要条件

3.2.1 练习1（需要画图）

3.2.2 练习2：（画图）

3.3 递归与迭代

3.3.1 求n的阶乘（不考虑溢出）

3.3.2 求第 n 个斐波那契数（不考虑溢出）

1.函数的嵌套调用和链式访问

函数和函数之间可以根据实际的需求进行组合的，也就是可以互相调用的。

1.1 嵌套调用

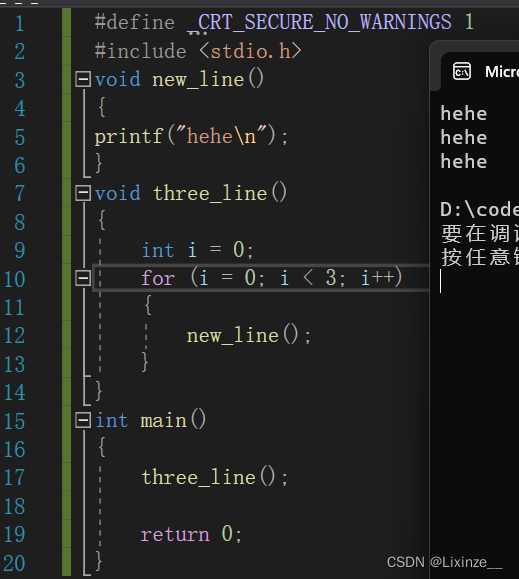
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>  
void new_line()
{
printf("hehe\n");
}
void three_line()
{
	int i = 0;  
	for (i = 0; i < 3; i++)
	{
		new_line();
	}
}
int main()
{
	three_line();  

	return 0;
}

函数可以嵌套调用，但是不能嵌套定义。

1.2 链式访问

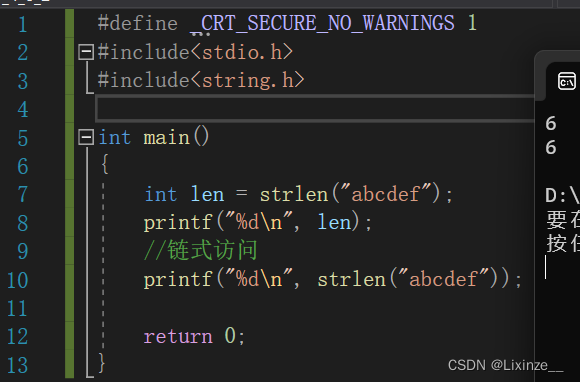
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<string.h>

int main()
{
	int len = strlen("abcdef");
	printf("%d\n", len);
	//链式访问
	printf("%d\n", strlen("abcdef"));

	return 0;
}
这是 printf 函数的返回值介绍，意思是这些函数的每一个都返回打印的字符数如果发生错误，则返回 -1.

链式访问的前提是函数要有返回值。

函数不写返回值时默认返回类型是 int。
//明确说明main函数不需要参数
//本质上main函数是有参数的
int main(void)
{
    return 0;
}
//main函数有3个参数
int main(int argc, char* argv[], char* envp[])
{
    return 0;
}

2. 函数的声明和定义

2.1 函数声明

1. 告诉编译器函数叫什么，参数类型是什么，返回类型是什么。但具体是不是存在，函数声明决定不了。

2. 函数的声明一般出现在函数的使用之前。要满足先声明后使用。

3. 函数的声明一般要放在头文件中的
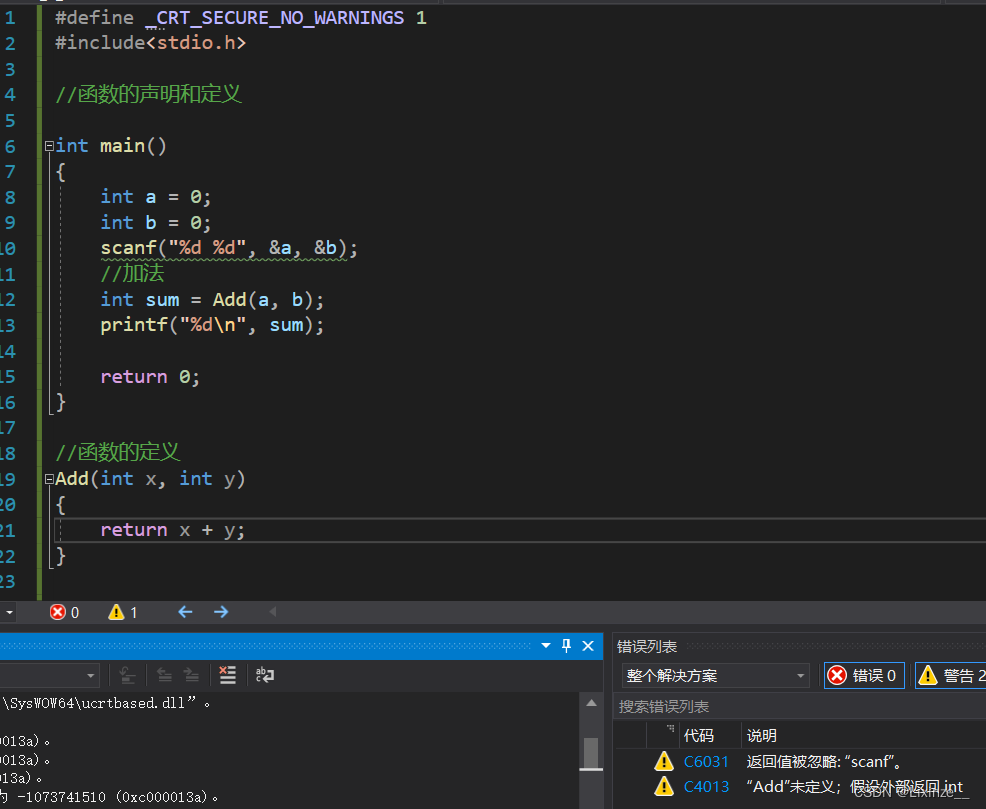
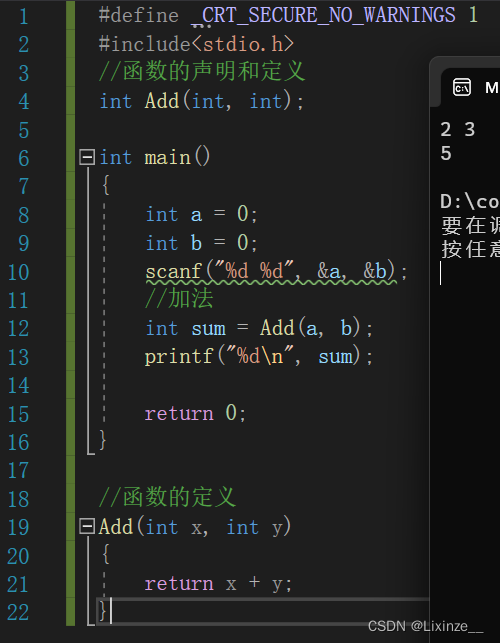
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//函数的声明和定义

int main()
{
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	//加法
	int sum = Add(a, b);
	printf("%d\n", sum);

	return 0;
}

//函数的定义
Add(int x, int y)
{
	return x + y;
}

2.2 函数定义

函数的定义是指函数的具体实现，交代函数的功能实现。

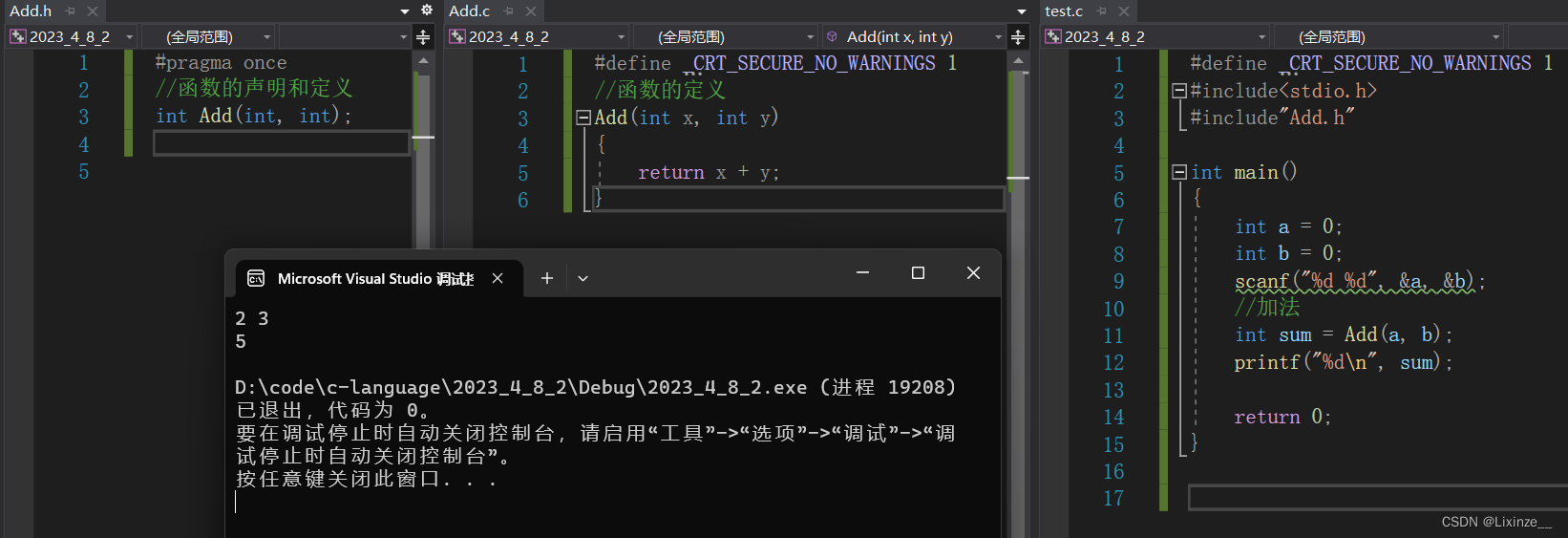
当我们正在写一个大型程序时，往往会需要写大量的函数来实现很多功能，如果声明和定义全部放到一个源程序文件中不利于我们调试和维护，分成三个文件分别为函数的声明、函数的定义、包含主函数的整体函数框架。这样可以使程序清晰，可读性大大增强。

3. 函数递归

3.1 什么是递归？

程序调用自身的编程技巧称为递归（recursion）。

递归作为一种算法在程序设计语言中广泛应用。

一个过程或函数在其定义或说明中有间接或直接调用自身的一种方法，它通常把一个大型复杂的问题转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程中所需要的多次重复计算，大大减少了程序的代码量。

递归的主要思考方式在于：把大事化小。

3.2 递归的两个必要条件

存在限制条件，当满足这个限制条件的时候，递归便不再继续。
每次递归调用之后越来越接近这个限制条件。

3.2.1 练习1（需要画图）

接收一个整型值（无符号），按照顺序打印它的每一位。

例如：

输入1234，输出1 2 3 4

首先先写一个不用递归的版本。

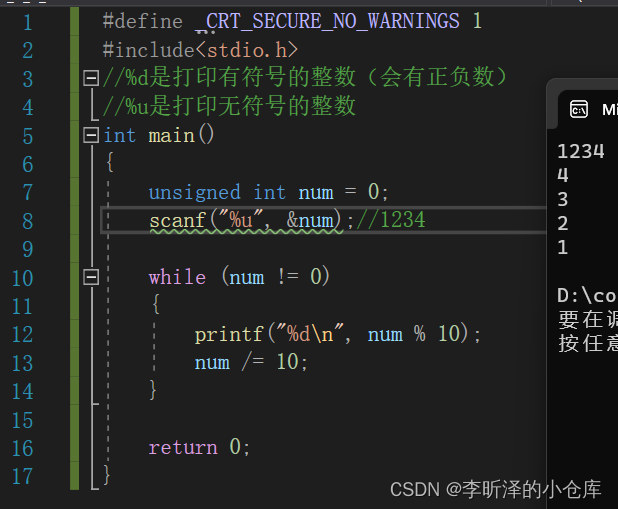
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//%d是打印有符号的整数（会有正负数）
//%u是打印无符号的整数
int main()
{
	unsigned int num = 0;
	scanf("%u", &num);//1234

	while (num != 0)
	{
		printf("%d\n", num % 10);
		num /= 10;
	}

	return 0;
}

如果用递归实现，我们的思路是大事化小。

//print(123)4
//print(12) 3 4
//print(1) 2 3 4
//1 2 3 4

就像剥洋葱一样层层打印。

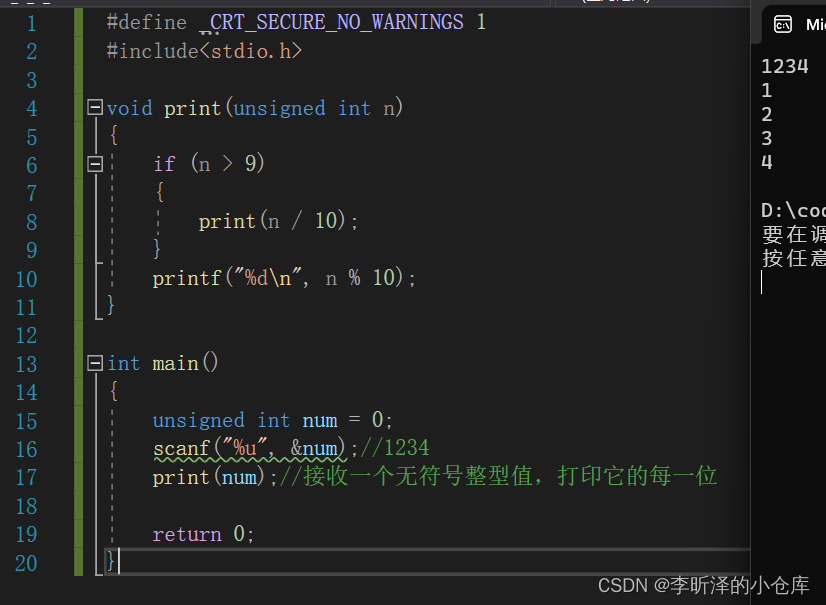
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

void print(unsigned int n)
{
	if (n > 9)
	{
		print(n / 10);
	}
	printf("%d\n", n % 10);
}

int main()
{
	unsigned int num = 0;
	scanf("%u", &num);//1234
	print(num);//接收一个无符号整型值，打印它的每一位

	return 0;
}

3.2.2 练习2：（画图）

编写函数不允许创建临时变量，求字符串的长度。

我们先写一个需要创建临时变量的版本：

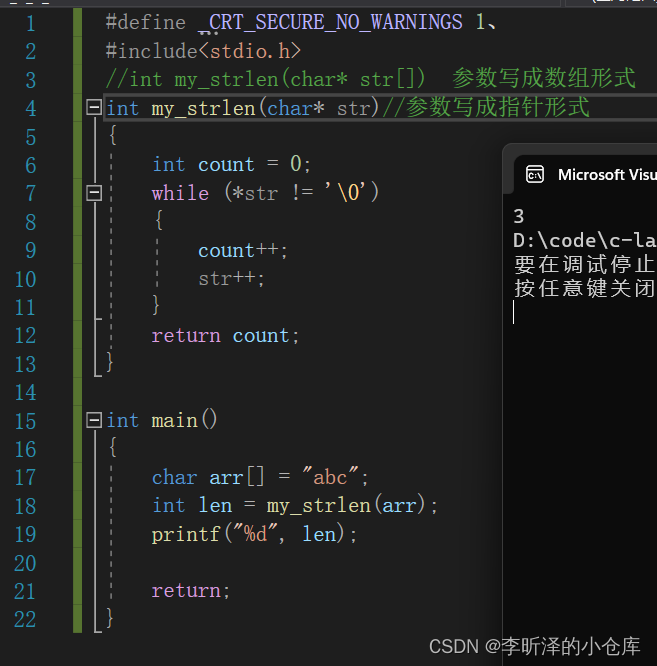
也就是模拟实现 strlen

#define _CRT_SECURE_NO_WARNINGS 1、
#include<stdio.h>
//int my_strlen(char* str[])  参数写成数组形式
int my_strlen(char* str)//参数写成指针形式
{
	int count = 0;
	while (*str != '\0')
	{
		count++;
		str++;
	}
	return count;
}

int main()
{
	char arr[] = "abc";
	int len = my_strlen(arr);
	printf("%d", len);

	return;
}

接下来我们用递归方式求解：

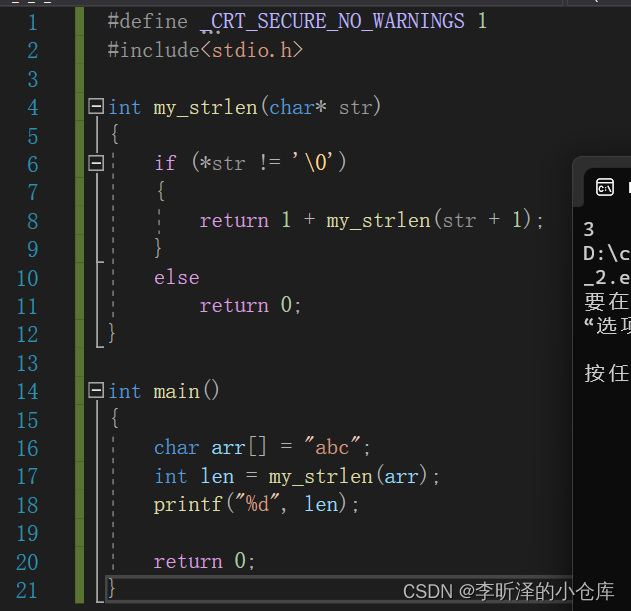
//my_strlen("abc")
//1+my_strlen("bc")
//1+1+my_strlen("c")
//1+1+1+my_strlen("")
//1+1+1+0

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

int my_strlen(char* str)
{
	if (*str != '\0')
	{
		return 1 + my_strlen(str + 1);
	}
	else
		return 0;
}

int main()
{
	char arr[] = "abc";
	int len = my_strlen(arr);
	printf("%d", len);

	return 0;
}

3.3 递归与迭代

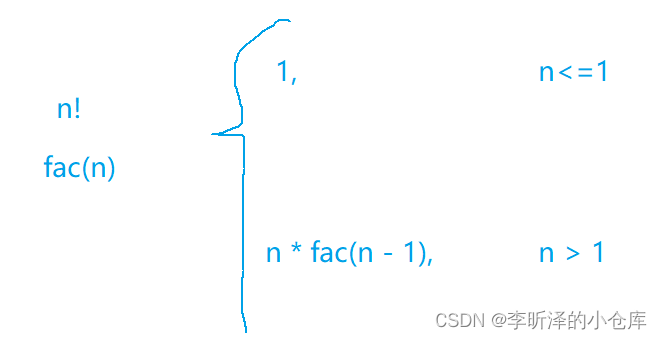
3.3.1 求n的阶乘（不考虑溢出）

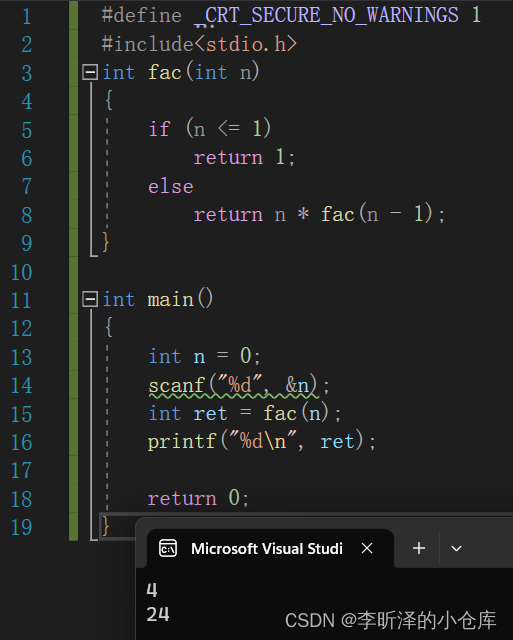
递归的方式：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int fac(int n)
{
	if (n <= 1)
		return 1;
	else
		return n * fac(n - 1);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = fac(n);
	printf("%d\n", ret);

	return 0;
}

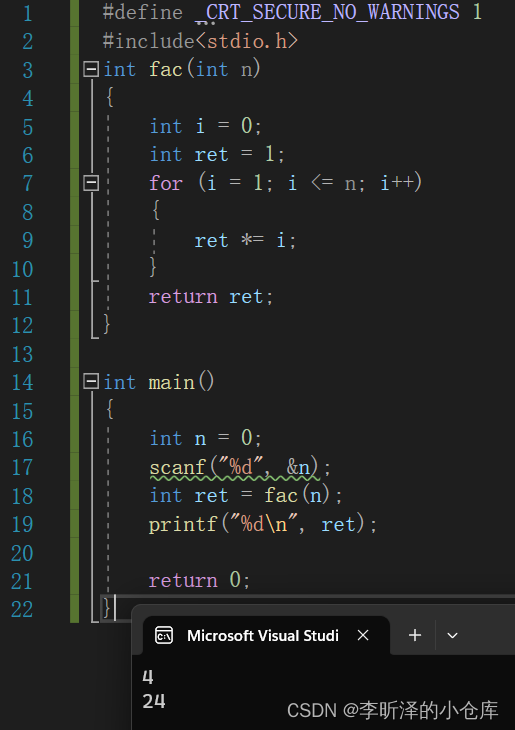
迭代的方式：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int fac(int n)
{
    int i = 0;
    int ret = 1;
    for (i = 1; i <= n; i++)
    {
        ret *= i;
    }
    return ret;
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    int ret = fac(n);
    printf("%d\n", ret);

    return 0;
}

3.3.2 求第 n 个斐波那契数（不考虑溢出）

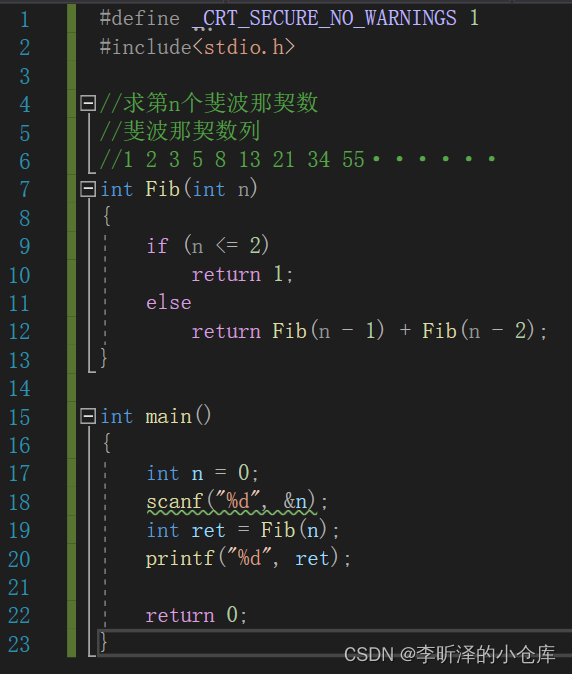
递归实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

//求第n个斐波那契数
//斐波那契数列
//1 2 3 5 8 13 21 34 55······
int Fib(int n)
{
	if (n <= 2)
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d", ret);

	return 0;
}

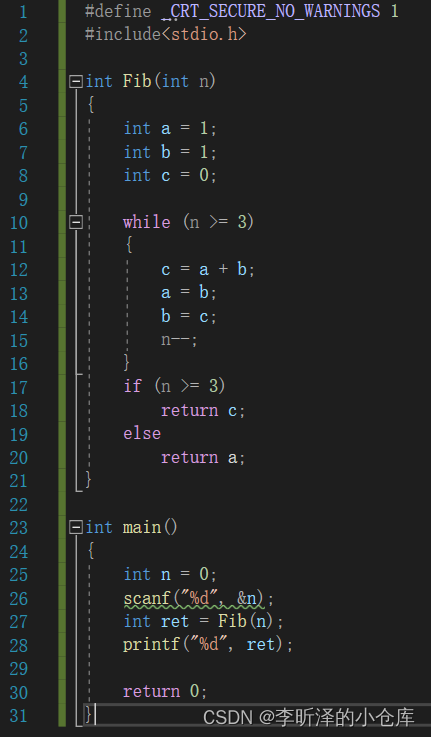
迭代实现：

在调试 factorial 函数的时候，如果你的参数比较大，那就会报错：

stack overflow（栈溢出）这样的信息。

系统分配给程序的栈空间是有限的，但是如果出现了死循环，或者（死递归），这样有可能导致一直开辟栈空间，最终产生栈空间耗尽的情况，这样的现象我们称之为栈溢出。

那如何解决上述的问题：

将递归写成非递归。

使用 stack 对象替代 nonstatic 局部对象。在递归函数设计中，可以使用 static 对象替代

nonstatic 局部对象（即栈对象），这不仅可以减少每次递归调用和返回时产生和释放

nonstatic 对象的开销，而且 static 对象还可以保存递归调用的中间状态，并且可为各个调用

层所访问。