目录

1 紧耦合、松耦合的区别

（1）紧耦合和松耦合的区别

（2）紧耦合和松耦合的分类

（3）为什么要使用紧耦合

2 SIFT和SUFT的区别

3 视差与深度的关系

4 闭环检测常用方法

5 描述PnP算法

6 梯度下降法、牛顿法、高斯-牛顿法的区别

7 什么是极线约束

8 单目视觉SLAM中尺寸漂移是怎么产生的

9 描述特征点法和直接法的优缺点

10 边缘检测算子有哪些？

---

1 紧耦合、松耦合的区别

（1）紧耦合和松耦合的区别

紧耦合：是把图像的特征加到特征向量中去，这样做优点是可以免去中间状态的累计误差，提高精度，缺点是系统状态向量的维数会非常高，需要很高的计算量；

松耦合：是把VO处理后获得的变换矩阵和IMU进行融合，这样做优点是计算量小但是会带来累计误差。

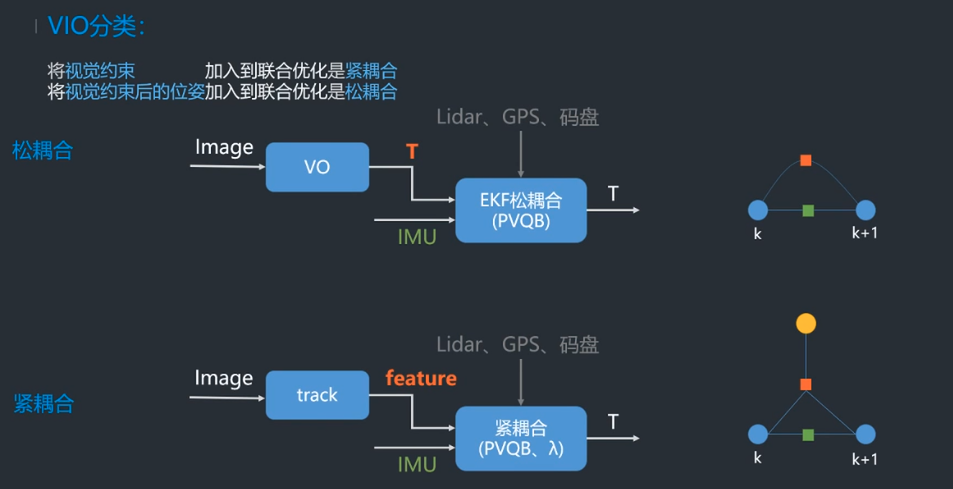
（2）紧耦合和松耦合的分类

vio	filter-based	optimization-based
紧耦合	MSCKF,ROVIO	OKVIS,VINS
松耦合	ssf,msf	Inertial Aided Dense & Semi-Dense Methods for Robust Direct Visual Odometry

（3）为什么要使用紧耦合

• 单纯凭（单目）视觉或IMU都不具备估计Pose的能力：视觉存在尺度不确定性、IMU存在零偏导致漂移；
• 松耦合中，视觉内部BA没有IMU的信息，在整体层面来看不是最优的。
• 紧耦合可以一次性建模所有的运动和测量信息，更容易达到最优。

2 SIFT和SUFT的区别

• 构建图像金字塔：SIFT特征利用不同尺寸的图像与高斯差分滤波器卷积；SURF特征利用原图片与不同尺寸的方框滤波器卷积。
• 特征描述子：SIFT特征有4×4×8=128维描述子，SURF特征有4×4×4=64维描述子。
• 特征点检测方法：SIFT特征先进行非极大抑制，再去除低对比度的点，再通过Hessian矩阵去除边缘响应过大的点；SURF特征先利用Hessian矩阵确定候选点，然后进行非极大抑制。
• 特征点主方向：SIFT特征在正方形区域内统计梯度幅值的直方图，直方图最大值对应主方向，可以有多个主方向；SURF特征在圆形区域内计算各个扇形范围内x、y方向的haar小波响应，模最大的扇形方向作为主方向。

3 视差与深度的关系

在相机完成校正后，则有 d / b = f / z,其中  表示左右图的横坐标之差，称为视差，b表示基线，f是焦距，z是深度。这个公式其实很好记，在深度和焦距确定的情况下，基线越大，视差也会越大。

4 闭环检测常用方法

ORB SLAM中采用的是词袋模型进行闭环检测筛选出候选帧，再通过求解Sim3判断最合适的关键帧。
LSD SLAM中的闭环检测主要是根据视差、关键帧连接关系，找出候选帧，然后对每个候选帧和测试的关键帧之间进行双向Sim3跟踪，如果求解出的两个李代数满足马氏距离在一定范围内，则认为是闭环成功。

5 描述PnP算法

已知空间点世界坐标系坐标和其像素投影，公式如下：

目前一共有两种解法，直接线性变换方法（一对点能够构造两个线性约束，因此12个自由度一共需要6对匹配点），另外一种就是非线性优化的方法，假设空间坐标点准确，根据最小重投影误差优化相机位姿。
目前有两个主要场景，其一是求解相机相对于某2维图像/3维物体的位姿；其二就是SLAM算法中估计相机位姿时通常需要PnP给出相机初始位姿。
在场景1中，我们通常输入的是物体在世界坐标系下的3D点以及这些3D点在图像上投影的2D点，因此求得的是相机坐标系相对于世界坐标系(Twc)的位姿
在场景2中，通常输入的是上一帧中的3D点（在上一帧的相机坐标系下表示的点）和这些3D点在当前帧中的投影得到的2D点，所以它求得的是当前帧相对于上一帧的位姿变换
 

6 梯度下降法、牛顿法、高斯-牛顿法的区别

在BA优化、PnP、直接法里面都有接触到非线性优化问题，上面几种方法都是针对对非线性优化问题提出的方法，将非线性最优化问题作如下展开，就可以获得梯度下降法和牛顿法

梯度下降法是一个一阶最优化算法，通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。因此指保留一阶梯度信息。缺点是过于贪心，容易走出锯齿路线。

牛顿法是一个二阶最优化算法，基本思想是利用迭代点处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似。因此保留二阶梯度信息。缺点是需要计算H矩阵，计算量太大。

而把非线性问题，先进行一阶展开，然后再作平方处理就可以得到高斯-牛顿法和列文博格方法

高斯-牛顿法对上式展开并对Δ x进行求导即可得高斯牛顿方程，其实其就是使用对牛顿法的H矩阵进行替换，但是有可能为奇异矩阵或变态，Δ x也会造成结果不稳定，因此稳定性差。

列文博格法就是在高斯-牛顿法的基础上对Δ x添加一个信赖区域，保证其只在展开点附近有效，即其优化问题变为带有不等式约束的优化问题，利用Lagrange乘子求解。

7 什么是极线约束

极线约束描述的是当同一个点投影到两个不同视角的图像上时，特征点、相机光心在投影模型下形成的约束，所谓极线约束就是说同一个点在两幅图像上的映射，已知左图映射点p1，那么右图映射点p2一定在相对于p1的极线上，这样可以减少待匹配的点数量。
如图所示， 两个相机光心连线为O1O2被称为基线，基线与像平面image1和image2的交点e1、e2被称为基点；平面PO1O2被称为极平面，极平面与像平面image1和image2的交线e1P1、e2P2被称为极线。
如果世界点P(未知)在image1上的特征点为P1(已知)，那么世界点P必定在P1O1O2所在平面上，即世界点P在image2上的像点必然在平面P1O1O2与像平面image2的交线e2P2上。这就是极线约束。

8 单目视觉SLAM中尺寸漂移是怎么产生的

用单目估计出来的位移，与真实世界相差一个比例，叫做尺度。这个比例在单目初始化时通过三角化确定，但单纯靠视觉无法确定这个比例到底有多大。由于SLAM过程中噪声的影响，这个比例还不是固定不变的。修正方式是通过回环检测计算Sim3进行修正。

9 描述特征点法和直接法的优缺点

特征点法

• 优点：1. 没有直接法的强假设，更加精确；2. 相较与直接法，可以在更快的运动下工作，鲁棒性好
• 缺点：1. 特征提取和特征匹配过程耗时长；2. 特征点少的场景中无法使用；3.只能构建稀疏地图

直接法

• 优点：1.省去了特征提取和特征匹配的时间，速度较快；2. 可以用在特征缺失的场合；3. 可以构建半稠密/稠密地图
• 缺点：1. 易受光照和模糊影响；2.运动必须慢；3.非凸性，易陷入局部极小解

10 边缘检测算子有哪些？

边缘检测一般分为三步，分别是滤波、增强、检测。基本原理都是用高斯滤波器进行去噪，之后在用卷积内核寻找像素梯度。常用有三种算法：canny算子，sobel算子，laplacian算子
canny算子：一种完善的边缘检测算法，抗噪能力强，用高斯滤波平滑图像，用一阶偏导的有限差分计算梯度的幅值和方向，对梯度幅值进行非极大值抑制，采用双阈值检测和连接边缘。
sobel算子：一阶导数算子，引入局部平均运算，对噪声具有平滑作用，抗噪声能力强，计算量较大，但定位精度不高，得到的边缘比较粗，适用于精度要求不高的场合。
laplacian算子：二阶微分算子，具有旋转不变性，容易受噪声影响，不能检测边缘的方向，一般不直接用于检测边缘，而是判断明暗变化。