基础知识
什么是贪心：贪心的本质是选择每一阶段的局部最优，从而达到全局最优。
但是贪心没有套路，做题的时候，只要想清楚 局部最优 是什么，如果推导出全局最优，其实就够了。
455.分发饼干
很容易想到，把孩子的胃口和饼干大小都排序，都从最小值开始遍历。如果最小的饼干无法满足最小的胃口，就换到相对大一点的饼干继续测试
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
int count = 0;
sort(g.begin(),g.end());
sort(s.begin(),s.end());
for(int i = 0,j = 0; i < g.size() && j < s.size();){
if(s[j] >= g[i]){
i++;
j++;
count++;
}
else if(s[j] < g[i])j++;
}
return count;
}
};
376. 摆动序列
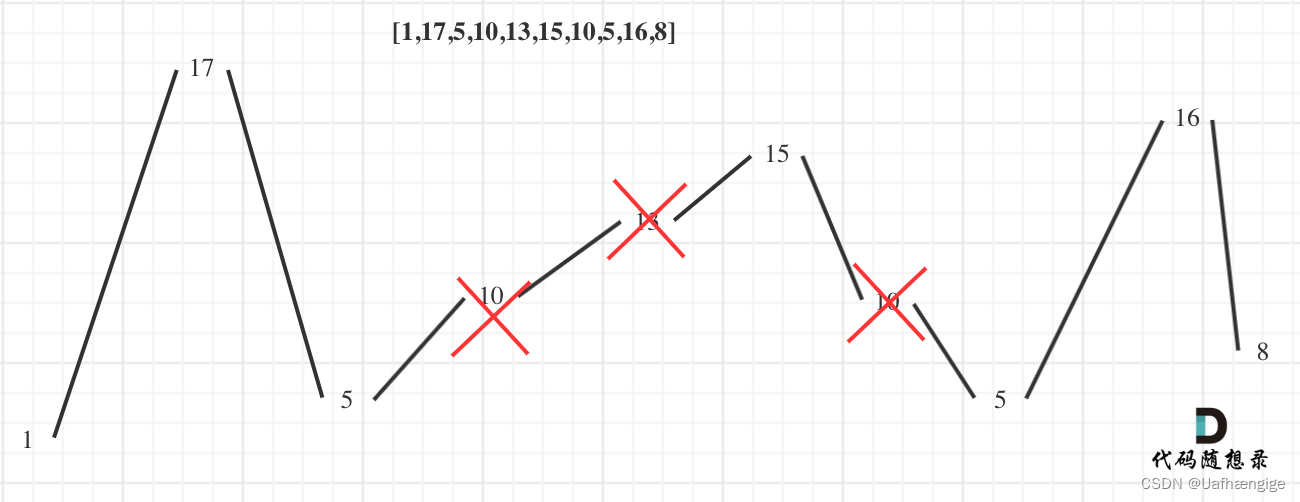局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。
整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。
核心就是上面的局部最优思路。接下来就是如何实现的问题。自己写的时候使用一个index来判断上一个是高峰还是低峰。然后将后序的值push进stack。要注意！！！一个序列如果所有值都相等，那size()==1的那个子序列可以看成只有一个峰值的摆动序列。，应该返回1而不是0。
stack 和 index实现：
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if(nums.size() <= 1)return nums.size();
if(nums.size() == 2 ){
if(nums[0] != nums[1]) return 2;
else return 1;
}
int index = 0;
stack<int> st;
int start = 1;
st.push(nums[0]);
for(start; start < nums.size();++start ){
if(nums[start] == nums[0]) continue;
if(nums[start] > nums[0]){
index = 1;
}
st.push(nums[start]);
break;
}
for(int i = start + 1; i < nums.size(); ++i){
if(nums[i] > st.top() && index == 0) {
st.push(nums[i]);
index = 1;
}
else if(nums[i] < st.top() && index == 1) {
st.push(nums[i]);
index = 0;
}
else{
st.pop();
st.push(nums[i]);
}
}
return st.size();
}
};
卡哥的实现：
最朴素的想法，i是当前元素的下标，
prediff = nums[i] - nums[i-1]，
curdiff = nums[i+1] - nums[i]；
(prediff > 0 && curdiff < 0) || (prediff < 0 && curdiff > 0)
res加一
但是一个序列会有多种情况
-
情况一：上下坡中有平坡
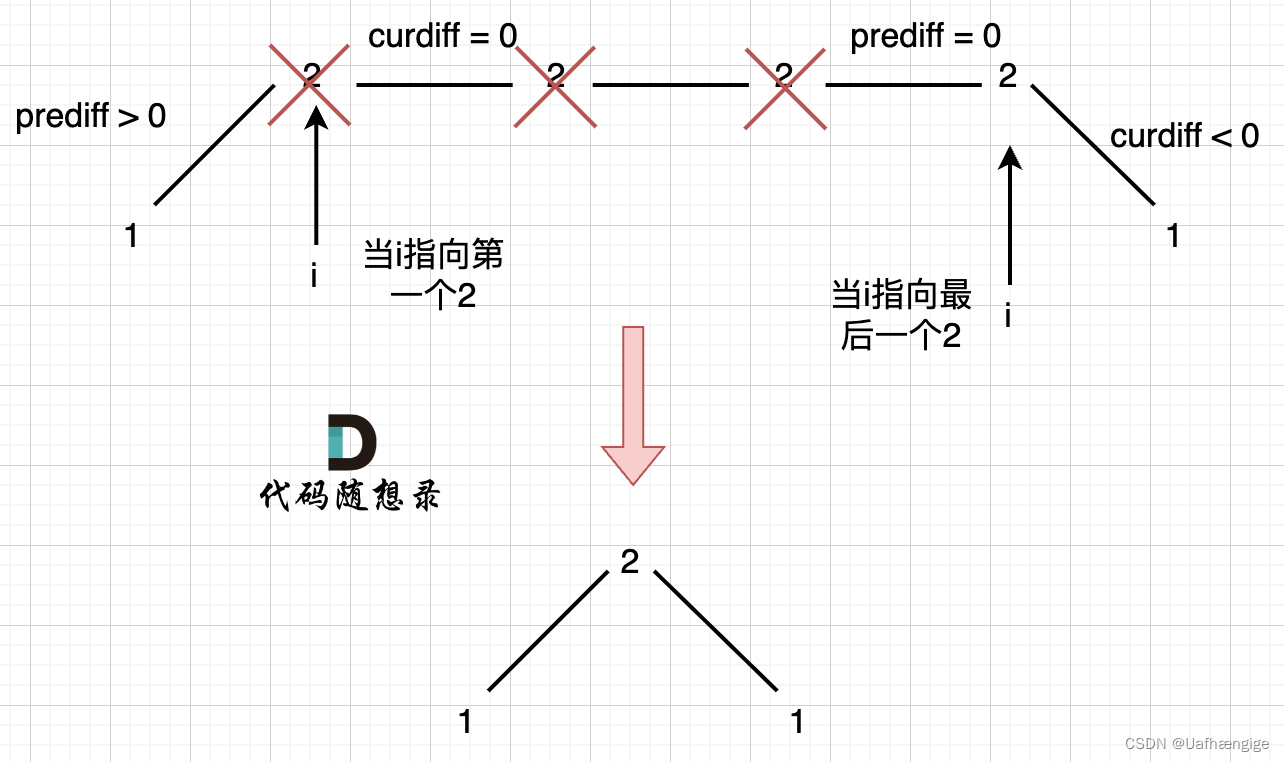
在图中，当i指向第一个2的时候，prediff > 0 && curdiff = 0 ，当 i 指向最后一个2的时候 prediff = 0 && curdiff < 0。
如果我们采用，删左面三个2的规则，那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值，因为他是把之前相同的元素都删掉留下的峰值。
所以我们记录峰值的条件应该是： (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，为什么这里允许 prediff == 0 ，就是为了 上面我说的这种情况。 -
情况二：数组首尾两端
首先，不管这个数组的大小是多少，只要大于等于2，就至少有一个大小为1的子序列，能够成为一个摆动序列。所以一开始res就被设置为1。在遍历数组的时候，i= 0开始， 因为要计算 curdiff = nums[i+1] - nums[i]； i < nums.size()-1。这意味着数组尾元素不会被遍历，但是没关系，res设置为1就是默认数组尾端是一个峰值。
下面看两种情况处理首元素：
1、[2,5]
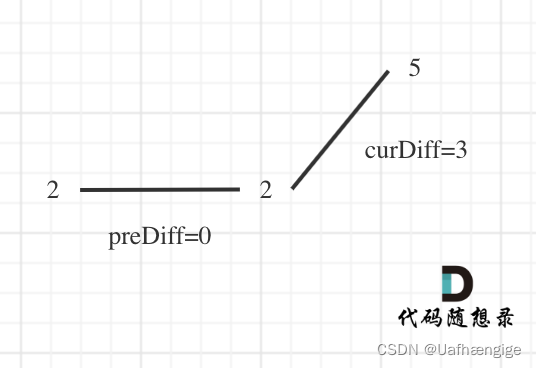针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即preDiff = 0。针对以上情形，result初始为1（默认最右面有一个峰值），此时curDiff > 0 && preDiff <= 0，那么result++（计算了左面的峰值），最后得到的result就是2（峰值个数为2即摆动序列长度为2）
2、[2,2]
这种情况其实就是平坡，index = 0 的地方 curDiff = prediff = 0不会统计。只到index = 1不会被遍历到，但是已经在最开始作为默认峰值统计到res中。
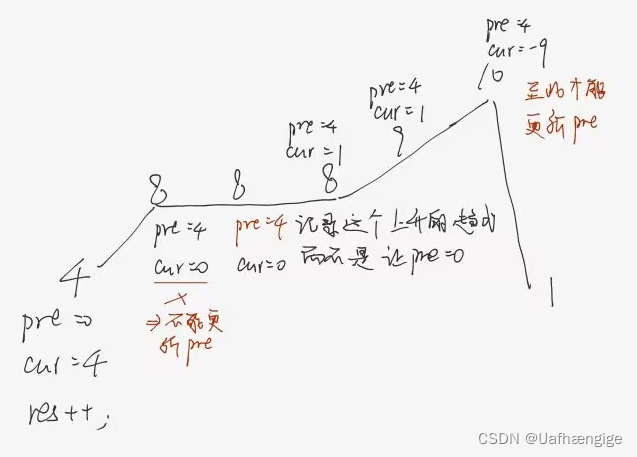
- 情况三：单调坡度有平坡
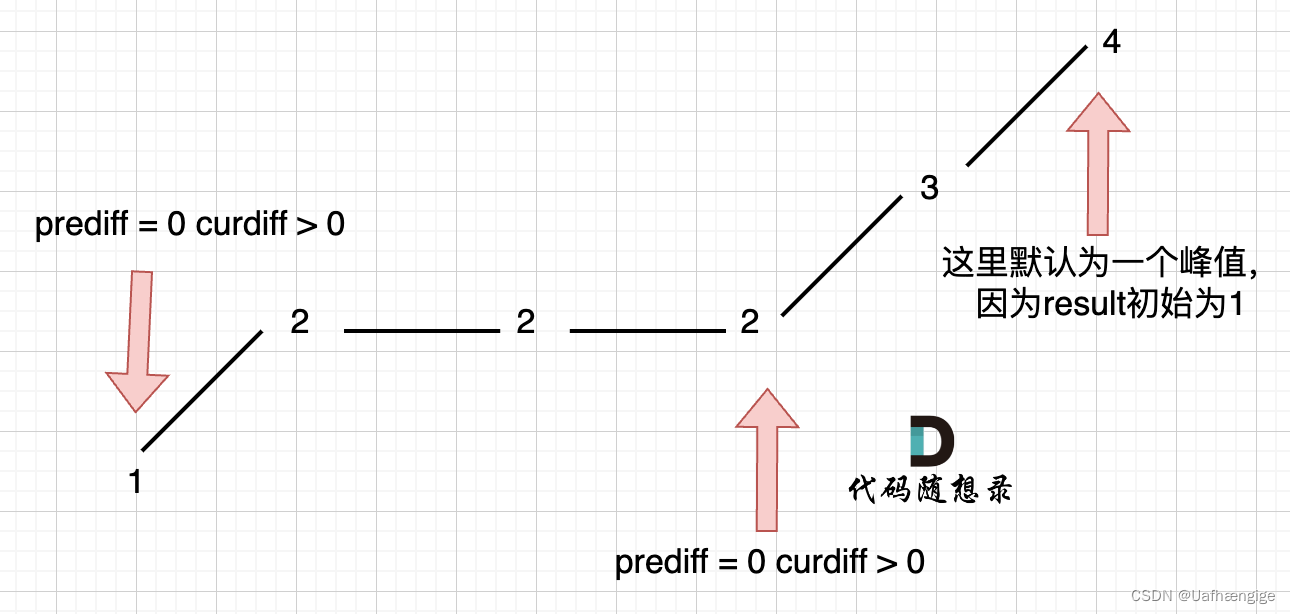上述情况会被统计三次。所以pre应当在有波动的时候才被更新。否则就保持原有的pre
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if(nums.size() <= 1) return nums.size();
int preDiff = 0;
int curDiff = 0;
int res = 1;
for(int i = 0 ; i < nums.size()-1; ++i){
curDiff = nums[i+1] - nums[i];
if((preDiff<=0 && curDiff>0) || (preDiff>=0 && curDiff<0)){
res++;
preDiff = curDiff;
}
}
return res;
}
};
53. 最大子数组和
暴力解法： 两层for循环，计算每一个子数组的和，记录最大值。
贪心：如果 -2 1 在一起，计算起点的时候，一定是从1开始计算，因为负数只会拉低总和，这就是贪心贪的地方！
局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。比如有元素 abcd，如果a+b>=0，a+b+c<0，那么无论ab取多少，只要取到c整体和就是一个负数。负数加上任何一个数，不管是正负还是0，都只会更小。
-5 + （-1） = -6
-1 + （-5） = -6。
-5 + 1 = -4
全局最优：选取最大“连续和”
局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。
其关键在于：不能让“连续和”为负数的时候加上下一个元素，而不是 不让“连续和”加上一个负数。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int sum = 0;
int res = INT_MIN;
for(int i = 0; i < nums.size(); ++i){
sum += nums[i];
if (sum > res) res = sum;
if(sum < 0) sum = 0;
}
return res;
}
};
