论文链接：https://arxiv.org/pdf/2010.13902.pdf

附录链接：https://yyou1996.github.io/files/neurips2020_graphcl_supplement.pdf 

代码链接：https://github.com/Shen-Lab/GraphCL 

1 图的数据增强

        我们专注于图级扩充。给定 M 个图的数据集中的图 G ∈ { : m ∈ M }，我们制定扩充图 G 满足： ，其中 q(·|G) 是扩充分布预定义的原始图，代表数据分布的人类先验。例如对于图像分类，旋转和裁剪的应用编码先验，人们将从旋转图像或其局部补丁中获得相同的基于分类的语义知识 [49, 50]

        在图表方面，可以遵循同样的想法。 1 是图形数据集是从不同领域抽象出来的，因此可能没有像图像数据集那样普遍适用的数据增强。换句话说，对于不同类别的图形数据集，某些数据扩充可能比其他数据扩充更受欢迎。我们主要关注三类：生化分子（例如化合物、蛋白质）[9]、社交网络[1]和图像超像素图[12]。接下来，我们为图结构数据提出了四种通用数据增强，并讨论了它们引入的直观先验。 

        节点丢弃

        给定图 G，节点丢弃将随机丢弃特定部分的顶点及其连接。它强制执行的潜在先验是顶点的缺失部分不会影响 G 的语义。每个节点的丢弃概率遵循默认的 i.i.d。均匀分布（或任何其他分布）。

        边缘扰动

        它会通过随机添加或删除一定比例的边来扰乱 G 中的连通性。这意味着 G 的语义对边连接模式方差具有一定的鲁棒性。我们也遵循 i.i.d.均匀分布以添加/删除每条边。

        属性掩码

        属性掩码提示模型使用上下文信息（即剩余属性）恢复被掩码的顶点属性。基本假设是缺少部分顶点属性不会对模型预测产生太大影响；

        子图

        这个使用随机游走从 G 中采样一个子图（该算法在附录 A 中进行了总结）。它假设 G 的语义可以在其（部分）局部结构中得到很好的保留。

        默认增强（丢弃、扰动、掩蔽和子图）比率设置为 0.2。

2 图对比学习

        受最近视觉表示学习中对比学习发展的推动（见第 2 节），我们提出了一个图对比学习框架（GraphCL）用于（自监督）GNN 预训练。

        在图对比学习中，预训练是通过潜在空间中的对比损失最大化同一图的两个增强视图之间的一致性来执行的，如图 1 所示。该框架由以下四个主要组件组成：

 （图对比学习的框架。两个图增强 qi(·|G) 和 qj (·|G) 从增强池 T 中采样并应用于输入图 G。一个共享的基于 GNN 的编码器 f (·) 和一个投影头 g(·) 被训练通过对比损失最大化表示 zi 和 zj 之间的一致性。）

        (1) 图数据扩充

        给定的图 G 经过图数据扩充以获得两个相关视图 ^Gi, ^Gj，作为正对，其中 分别。对于图数据集的不同领域，如何从战略上选择数据扩充很重要（第 4 节）；

        (2) 基于 GNN 的编码器

        基于 GNN 的编码器 f (·)（在 (2) 中定义）提取图级表示向量 hi, hj 用于增强图 ^Gi, ^Gj。图对比学习不对 GNN 架构施加任何约束。

         (3) 投影头

        正如 [18] 中所提倡的，名为 projection head 的非线性变换 g(·) 将增强表示映射到计算对比损失的另一个潜在空间。在图对比学习中，应用双层感知器 (MLP) 来获得 zi, zj 。

        (4) 对比损失函数

        对比损失函数 L(·) 被定义为强制最大化正对 zi、zj 与负对之间的一致性。在这里，我们利用归一化温度标度交叉熵损失 (NT-Xent) [51、25、52]。

        在 GNN 预训练过程中，通过对比学习随机抽取 N 个图的 minibatch 进行处理，得到 2N 个增广图和相应的对比损失进行优化，其中我们将 zi, zj 重新标注为 用于小批量中的第 n 个图。负对不是明确采样的，而是从与 [53、18] 中相同的小批量中的其他 N-1 个扩充图中生成的。将余弦相似度函数表示为 ，第 n 个图的 NT-Xent 定义为：

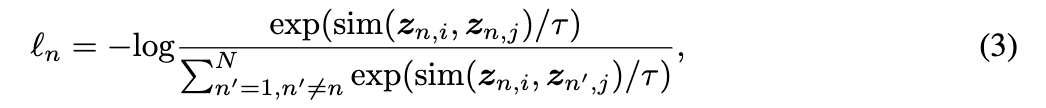
         其中 τ 表示温度参数。最终的损失计算在所有正对在minibatch上。所提出的图形对比学习方法总结在附录 A 中。

        讨论

        我们首先证明 GraphCL 可以被视为两种增强图的潜在表示之间的互信息最大化的一种方式。完整的推导在附录 F 中，损失形式重写如下：

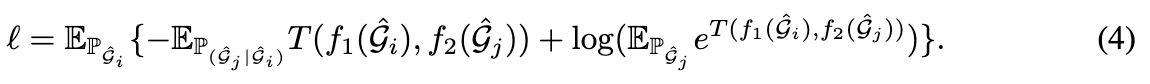
        上述损失本质上最大化了 之间互信息的下界，即 的组合决定了我们期望的视图。此外，我们绘制了 GraphCL 与最近提出的对比学习方法之间的联系，我们证明 GraphCL 可以重写为一个通用框架，通过重新解释 (4) 统一图结构数据上的广泛对比学习方法。在我们的实现中，我们选择 f1 = f2 并通过数据扩充生成 ^Gi, ^Gj，而组合的各种选择导致 (4) 实例化为其他特定的对比学习算法，包括 [54, 55, 56, 21, 57, 58 , 59] 也显示在附录 F

 上述损失公式推理步骤：

 

        其中 P( ^Gi, ^Gj ), P( ^Gj | ^Gi), P^Gi 分别是增强图的联合分布、条件分布和边缘分布，T(·,·) 是一个可学习的得分函数，我们用相似函数 sim( ·,·), 温度系数 τ 和投影头 g(·)。因此，(3) 符合 InfoNCE 损失 [6, 7] 的公式，使得最小化 (3) 等效于最大化图  的两个视图的潜在表示之间的互信息的下限。我们想强调投影头在框架中的关键作用，它提供可学习的权重来为得分函数构建函数空间，与丢弃投影头相比达到更严格的下界（它的关键作用也在[3]中进行了经验验证）。