本节的任务是使用Markov模型对后续序列进行预测,使用sin函数+噪声绘制1000个样本点,取tau为4,即利用后四个的信息预测第五个。
目录
1.构造样本点
2.抽取iter
3.构造网络
4.训练
5.预测
5.1单步
5.1多步
1.构造样本点
T = 1000 # 总共产⽣1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3)) 要生成features-label对,y=xt,Xt=[xt-tau,...xt-1]。由于前tau个样本没有足够的前tau个数据来预测,所以去掉为(T-tau)。
x是一个(1000,)的tensor,表示的是上图的函数值,也就是label(y)!!
tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):
features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))features是一个(996,4)的tensor,一开始是全零,后面赋予的四列分别为x的[0,996];[1,997];[2,998];[3,999];[4,1000];这样才能保证每一行都是前后的tau个数据!!!
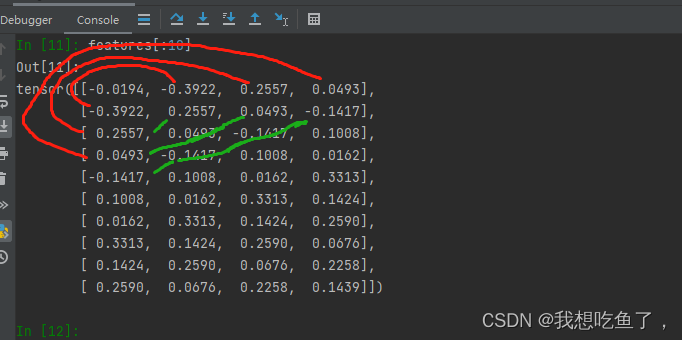
2.抽取iter
用d2l里面自带的load_array函数,传入样本和label,自动返回bs个。
在此,只取前600个用于训练。
batch_size, n_train = 16, 600
# 只有前n_train个样本⽤于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
batch_size, is_train=True)看下源码加深印象,其实也就是常规的dataset和dataloader:
def load_array(data_arrays, batch_size, is_train=True):
"""Construct a PyTorch data iterator.
Defined in :numref:`sec_linear_concise`"""
dataset = data.TensorDataset(*data_arrays)
return data.DataLoader(dataset, batch_size, shuffle=is_train)3.构造网络
用一个简单的MLP
# 初始化⽹络权重的函数
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
# ⼀个简单的多层感知机
def get_net():
net = nn.Sequential(nn.Linear(4, 10),
nn.ReLU(),
nn.Linear(10, 1))
net.apply(init_weights)
return net
# 平⽅损失。注意:MSELoss计算平⽅误差时不带系数1/2
loss = nn.MSELoss(reduction='none')4.训练
def train(net, train_iter, loss, epochs, lr):
trainer = torch.optim.Adam(net.parameters(), lr)
for epoch in range(epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.sum().backward()
trainer.step()
print(f'epoch {epoch + 1}, '
f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')
net = get_net()
train(net, train_iter, loss, 5, 0.01)5.预测
5.1单步
下面的代码注意,这里的features是包含了原1000个样本点的features,所以net用600训练后,这里onestep_preds是将原数据中的所有features喂进去:
onestep_preds = net(features)
d2l.plot([time, time[tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
'x', legend=['data', '1-step preds'], xlim=[1, 1000],
figsize=(6, 3))5.1多步
而其余的多步预测,则是使用自己的预测数据作为新feature来预测:
multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
multistep_preds[i] = net(
multistep_preds[i - tau:i].reshape((1, -1)))
d2l.plot([time, time[tau:], time[n_train + tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy(),
multistep_preds[n_train + tau:].detach().numpy()], 'time',
'x', legend=['data', '1-step preds', 'multistep preds'],
xlim=[1, 1000], figsize=(6, 3))上面的reshape(1,-1),bs=1因为每次只需返回一个值!
注意:上面的multistep_preds前604个与x是一样的,后面的是0,根据前面的和预测值预测(预测了tau个后就完全依据预测值预测了)
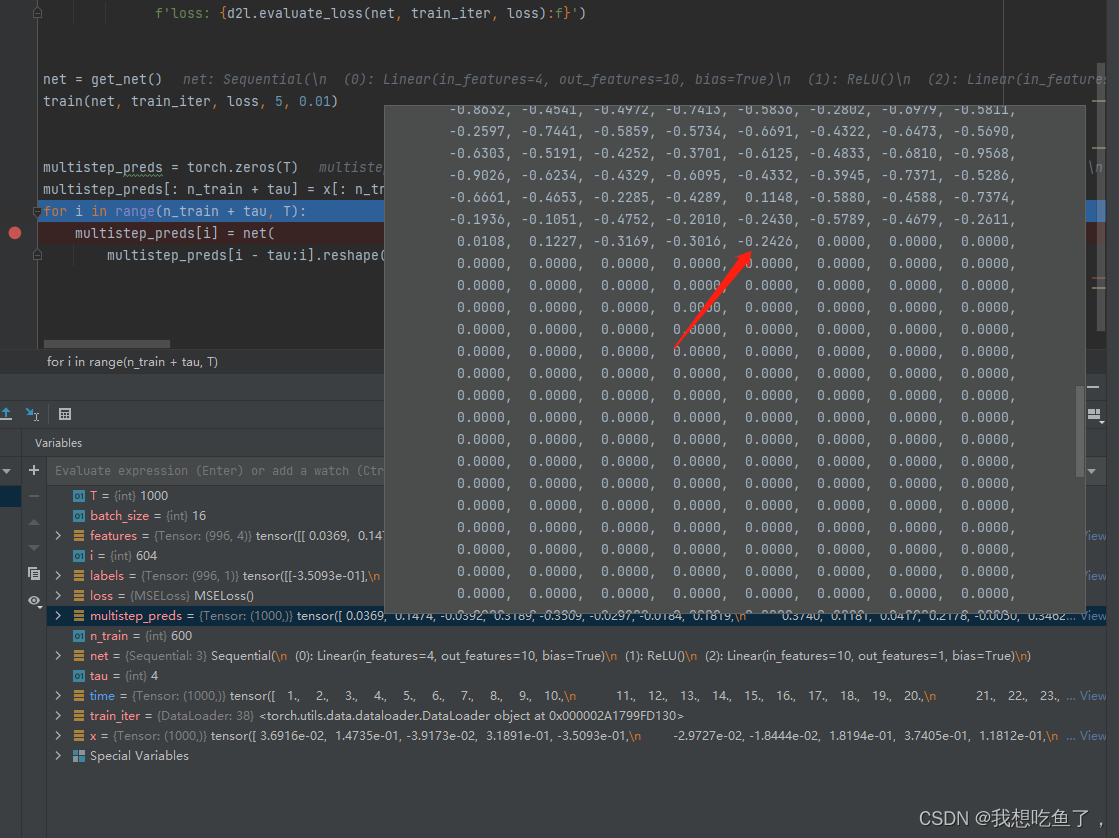
5.3K布预测
使用预测出的数据当后续预测的样本,进而继续预测。这会导致误差累积,偏差较大。
max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# 列i(i<tau)是来⾃x的观测,其时间步从(i+1)到(i+T-tau-max_steps+1)
for i in range(tau):
features[:, i] = x[i: i + T - tau - max_steps + 1]
# 列i(i>=tau)是来⾃(i-tau+1)步的预测,其时间步从(i+1)到(i+T-tau-max_steps+1)
for i in range(tau, tau + max_steps):
features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
[features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
figsize=(6, 3))